Aufgaben:Aufgabe 4.14: AKF und KKF bei Rechtecksignalen: Unterschied zwischen den Versionen
| Zeile 44: | Zeile 44: | ||
| − | {Es gelte wieder $p = 0.25$. Berechnen Sie die Kreuzkorrelationsfunktion $\varphi_{pz}(\tau)$ | + | {Es gelte wieder $p = 0.25$. Berechnen Sie die Kreuzkorrelationsfunktion $\varphi_{pz}(\tau)$ für $\tau = 0$, $\tau = 3T$ und $\tau = 6T$? |
|type="{}"} | |type="{}"} | ||
$\varphi_{pz}(\tau= 0) \ = $ { -0.26--0.24 } $\ \rm V^2$ | $\varphi_{pz}(\tau= 0) \ = $ { -0.26--0.24 } $\ \rm V^2$ | ||
| Zeile 69: | Zeile 69: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Der AKF-Wert bei | + | '''(1)''' Der AKF-Wert bei $\tau = 0$ gibt die mittlere Leistung an: |
| − | :$$\varphi_z ( \tau = 0) = | + | :$$\varphi_z ( \tau = 0) = {1}/{2} \cdot (1 {\rm V})^2 \hspace{0.15cm}\underline{= 0.5 {\rm V}^2}.$$ |
| − | Für | + | Für $\tau = \pm T$, $\underline{\tau = \pm 3T}$, ... ergibt sich $\varphi_z ( \tau)\hspace{0.15cm}\underline{ = 0}$. |
| − | |||
| − | + | Für die Zwischenwerte $\tau = \pm 2T$, $\tau = \pm 4T$, $\underline{\tau = \pm 6T}$, ... gilt: | |
| + | :$$\varphi_z ( \tau) = \frac {1 {\rm V}^2}{2} \left(p \hspace{0.02cm} \cdot \hspace{0.02cm}p \hspace{0.2cm} + \hspace{0.2cm}p \hspace{0.02cm}\cdot \hspace{0.02cm}(p-1) \hspace{0.2cm}+\hspace{0.2cm} (p-1)\hspace{0.02cm} \cdot \hspace{0.02cm}p \hspace{0.2cm}+\hspace{0.2cm} (p-1)\hspace{0.02cm} \cdot \hspace{0.02cm}(p-1)\right) = \hspace{0.1cm}... \hspace{0.1cm}= 0.5\, {\rm V}^2 \cdot (1-2p)^2 .$$ | ||
| − | + | [[Datei:P_ID437__Sto_A_4_14_a.png|framed|right|AKF und KKF]] | |
| − | + | Hierbei steht $p$ für $p \cdot (+1)$ und $(p-1)$ für $(1-p) \cdot (-1)$, also jeweils Wahrscheinlichkeit mal normierter Amplitudenwert. Mit $p = 0.25$ ergeben sich diese Zwischenwerte zu $\varphi_z ( \tau = \pm 6 T) \hspace{0.15cm}\underline{=0.125 \rm V^2}$. | |
| − | '''(2)''' | + | Die Skizze zeigt den Verlauf von $\varphi_z(\tau)$ für $p = 0.25$ im Bereich von $-7T \le \tau \le +7T$ als blaue Kurve. |
| + | *Aufgrund des rechteckförmigen Signalverlaufs ergibt sich eine Summe von Dreieckfunktionen. | ||
| + | *Für $p = 0.5$ würden die äußeren (kleineren) Dreiecke verschwinden. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Die AKF $\varphi_p(\tau)$ des unipolaren periodischen Signals $p(t)$ ist in der allgemeingültigen Darstellung von (1) ⇒ AKF $\varphi_z(\tau)$ als Sonderfall für $p = 1$ enthalten. Man erhält nun eine periodische AKF (siehe roter Kurvenverlauf in obiger Skizze) mit | ||
:$$\varphi_p ( \tau = 0) = \varphi_p ( \tau = \pm 2 T) = \varphi_p ( \tau = \pm 4 T) = \hspace{0.1cm} ... \hspace{0.1cm}\hspace{0.15cm}\underline{= 0.5 {\rm V}^2},$$ | :$$\varphi_p ( \tau = 0) = \varphi_p ( \tau = \pm 2 T) = \varphi_p ( \tau = \pm 4 T) = \hspace{0.1cm} ... \hspace{0.1cm}\hspace{0.15cm}\underline{= 0.5 {\rm V}^2},$$ | ||
:$$\varphi_p ( \tau = \pm T) = \varphi_p ( \tau = \pm 3T) = \hspace{0.1cm} ... \hspace{0.1cm}\hspace{0.15cm}\underline{= 0}.$$ | :$$\varphi_p ( \tau = \pm T) = \varphi_p ( \tau = \pm 3T) = \hspace{0.1cm} ... \hspace{0.1cm}\hspace{0.15cm}\underline{= 0}.$$ | ||
| − | |||
| − | |||
| − | :Man erhält mit | + | '''(3)''' Auch für die KKF ergibt sich für $\tau = \pm T$, $\underline{\tau = \pm 3T}$, ... , ... stets der Wert $0$. Dagegen sind die KKF-Werte für $\tau = \pm 2T$, $\tau = \pm 2T$, ... identisch mit denen bei $\tau = 0$: |
| + | :$$\varphi_{pz} ( \tau = 0) = \varphi_{pz} ( \tau = \pm 2 T) = \varphi_{pz} ( \tau = \pm 4 T) = \hspace{0.1cm} ... \hspace{0.1cm}= \frac {1 {\rm V}^2}{2} \left( p - (1-p)\right) = \frac {2p -1}{2}\, {\rm V}^2 .$$ | ||
| + | |||
| + | Man erhält mit $p = 0.25$ folgende Ergebnisse (siehe grüne Kurve in obiger Skizze): | ||
:$$\varphi_{pz} ( \tau = 0)\hspace{0.15cm}\underline{= -0.25 {\rm V}^2},\hspace{0.5cm} | :$$\varphi_{pz} ( \tau = 0)\hspace{0.15cm}\underline{= -0.25 {\rm V}^2},\hspace{0.5cm} | ||
\varphi_{pz} ( \tau = 3T)\hspace{0.15cm}\underline{= 0},\hspace{0.5cm} | \varphi_{pz} ( \tau = 3T)\hspace{0.15cm}\underline{= 0},\hspace{0.5cm} | ||
\varphi_{pz} ( \tau = 6T)\hspace{0.15cm}\underline{= -0.25 {\rm V}^2}.$$ | \varphi_{pz} ( \tau = 6T)\hspace{0.15cm}\underline{= -0.25 {\rm V}^2}.$$ | ||
| − | + | *Mit $p = 1$ würde dagegen $z(z) \equiv p(t)$gelten und damit natürlich auch $\varphi_{pz}(\tau) \equiv \varphi_{p}(\tau) \equiv \varphi_{z}(\tau)$. | |
| + | *Für den Sonderfall $p = 0.5$ ergäbe sich keine Korrelation zwischen $p(t)$ und $z(t)$ und damit $\varphi_{pz}(\tau)=0$. | ||
| − | '''(4)''' Durch Einsetzen von | + | |
| − | :$$\varphi_c ( \tau ) = \overline{c(t)\hspace{0.02cm} \cdot \hspace{0.02cm} c(t + \tau)} = \overline{a(t)\hspace{0.02cm} \cdot \hspace{0.02cm} a(t + \tau)} \hspace{0.1cm}+\hspace{0.1cm}\overline{a(t)\hspace{0.02cm} \cdot \hspace{0.02cm} b(t + \tau)} | + | '''(4)''' Durch Einsetzen von $c(t) = a(t) + b(t)$ in die allgemeine AKF-Definition erhält man: |
| + | :$$\varphi_c ( \tau ) = \overline{c(t)\hspace{0.02cm} \cdot \hspace{0.02cm} c(t + \tau)} = \overline{a(t)\hspace{0.02cm} \cdot \hspace{0.02cm} a(t + \tau)} \hspace{0.1cm}+\hspace{0.1cm}\overline{a(t)\hspace{0.02cm} \cdot \hspace{0.02cm} b(t + \tau)} +\overline{b(t)\hspace{0.02cm} \cdot \hspace{0.02cm} a(t + \tau)} \hspace{0.1cm}+\hspace{0.1cm}\overline{b(t)\hspace{0.02cm} \cdot \hspace{0.02cm} b(t + \tau)}. $$ | ||
:$$\Rightarrow \hspace{0.5cm} \varphi_c ( \tau ) = \varphi_{a} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{ab} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{ba} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm}\varphi_{a} ( \tau ). $$ | :$$\Rightarrow \hspace{0.5cm} \varphi_c ( \tau ) = \varphi_{a} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{ab} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{ba} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm}\varphi_{a} ( \tau ). $$ | ||
| − | + | Richtig ist somit der <u>Lösungsvorschlag 2</u>. | |
| − | + | *Der Lösungsvorschlag 1 trifft nur zu, wenn $a(t)$ und $b(t)$ unkorreliert sind. | |
| + | *Der letzte Vorschlag, die Faltungsoperation, ist immer falsch. Eine ähnliche Gleichung würde sich nur dann ergeben, wenn wir die WDF $f_c(c)$ der Summe $c(t) = a(t) + b(t)$ betrachten und $a(t)$ und $b(t)$) statistisch unabhängig sind: $f_c (c) = f_a (a) \star f_b (b) .$ | ||
'''(5)''' Mit dem Ergebnis von (4) und unter Berücksichtigung des Faktors 1/2 erhält man: | '''(5)''' Mit dem Ergebnis von (4) und unter Berücksichtigung des Faktors 1/2 erhält man: | ||
| − | :$$\varphi_s ( \tau ) = | + | :$$\varphi_s ( \tau ) = {1}/{4} \cdot \left[ \varphi_{p} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{z} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} 2 \cdot \varphi_{pz} ( \tau ) \right] . $$ |
| − | |||
| − | |||
| − | |||
| − | :Mit | + | Hierbei ist bereits berücksichtigt, dass die KKF zwischen $p(t)$ und $z(t)$ eine gerade Funktion ist, so dass auch $\varphi_{pz}(\tau) = \varphi_{zp}(\tau)$ gilt. Für $\tau = 0$ erhält man deshalb mit den obigen Ergebnissen allgemein: |
| + | :$$\varphi_s( \tau = 0) = {1}/{4} \cdot \left( 0.5 {\rm V}^2 +0.5 {\rm V}^2 + 2 \cdot \frac{2p-1}{2} {\rm V}^2\right) .$$ | ||
| + | Mit $p = 0.25$ ergibt sich $ \varphi_{pz} ( \tau = 0 ) = 0.125\rm V^2$. Dieses Ergebnis ist plausibel. Im Mittel ist nur in jedem achten Intervall $s(t)=1 \hspace{0.05cm} \rm V$; ansonsten ist $s(t)=0 \hspace{0.05cm} \rm V$. | ||
| − | + | Für geradzahlige Vielfache von $T$ gilt: | |
| − | :$$ \varphi_s ( \tau = \pm 2 T) = \varphi_s ( \tau = \pm 4 T) = \hspace{0.1cm} ... \hspace{0.1cm} = | + | :$$ \varphi_s ( \tau = \pm 2 T) = \varphi_s ( \tau = \pm 4 T) = \hspace{0.1cm} ... \hspace{0.1cm} = \frac {0.5 {\rm V}^2}{4} \left( (1-2p)^2 +1 + 2 \cdot (2p -1)\right) = 0.5 \, {\rm V}^2 \hspace{0.02cm} \cdot \hspace{0.02cm} p^2.$$ |
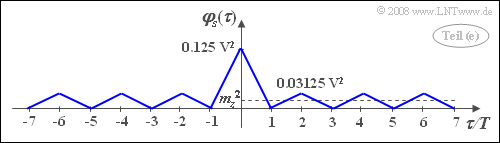
| − | + | Mit $p = 0.5$ erhält man hierfür den Wert $0.03125 \hspace{0.1cm}V^2$. Alle AKF-Werte bei ungeradzahligen Vielfachen von $T$ sind wieder $0$. Damit ergibt sich der skizzierte AKF-Verlauf. Die gesuchten Zahlenwerte sind somit: | |
| − | [[Datei:P_ID441__Sto_A_4_14_e.png| | + | [[Datei:P_ID441__Sto_A_4_14_e.png|framed|right|AKF eines unipolaren Rechtecksignals]] |
| − | + | :$$\varphi_{s} ( \tau = 0)\hspace{0.15cm}\underline{= 0.125 {\rm V}^2},$$ | |
| − | :$$\varphi_{s} ( \tau = 0)\hspace{0.15cm}\underline{= 0.125 {\rm V}^2}, | + | :$$\varphi_{s} ( \tau = 3T)\hspace{0.15cm}\underline{= 0},$$ |
| − | \varphi_{s} ( \tau = 3T)\hspace{0.15cm}\underline{= 0}, | + | :$$\varphi_{s} ( \tau = 6T)\hspace{0.15cm}\underline{= -0.03125 {\rm V}^2}.$$ |
| − | \varphi_{s} ( \tau = 6T)\hspace{0.15cm}\underline{= -0.03125 {\rm V}^2}.$$ | ||
| − | + | Ein Vergleich mit der Skizze zur Teilaufgabe (1) zeigt, dass das binäre Signal $s(t)$ bis auf den Faktor $1/4$ die gleiche AKF aufweist wie das Ternärsignal $z(t)$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Aufgaben zu Stochastische Signaltheorie|^4.6 KKF und Kreuzleistungsdichte^]] | [[Category:Aufgaben zu Stochastische Signaltheorie|^4.6 KKF und Kreuzleistungsdichte^]] | ||
Version vom 30. März 2017, 11:47 Uhr
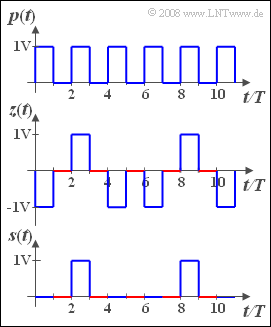
Wir betrachten ein periodisches Rechtecksignal $p(t)$ entsprechend der oberen Skizze mit den beiden möglichen Amplitudenwerten $0 \hspace{0.05cm} \rm V$ und $1 \hspace{0.05cm} \rm V$ und der Rechteckdauer $T$. Die Periodendauer beträgt somit $T_0 = 2T$.
Darunter ist das Zufallssignal $z(t)$ gezeichnet.
- Dieses ist zwischen $(2i-1)T$ und $2i T$ mit $i=$ ... , $-1, 0, +1$, ... (im Bild rot hervorgehoben) jeweils $z(t)=0 \hspace{0.05cm} \rm V$.
- Dagegen ist in den blau gezeichneten Intervallen zwischen $(2i+1) \cdot T$ der Signalwert zweipunktverteilt $\pm 1 \hspace{0.05cm} \rm V$.
Die Wahrscheinlichkeit, dass in den blau dargestellten Intervallen $z(t)=+1 \hspace{0.05cm} \rm V$ gilt, sei allgemein gleich $p$ und unabhängig von den vorher ausgewürfelten Werten.
Das unterste Signal in nebenstehender Grafik kann aus den beiden ersten konstruiert werden. Es gilt:
- $$s(t) = {1}/{2} \cdot [p(t) + z(t)].$$
In den rot eingezeichneten Zeitintervallen zwischen $(2i-1)T$ und $2i T$ ($i$ ganzzahlig) gilt $s(t)=0 \hspace{0.05cm} \rm V$, da hier sowohl $p(t)$ als auch $z(t)$ gleich $0$ sind. In den dazwischen liegenden Intervallen ist der Amplitudenwert zweipunktverteilt zwischen $0 \hspace{0.05cm} \rm V$ und $1 \hspace{0.05cm} \rm V$, wobei der Wert $1 \hspace{0.05cm} \rm V$ wieder mit der Wahrscheinlichkeit $p$ auftritt.
Oder anders ausgedrückt: Die Signale $z(t)$ und $s(t)$ sind äquivalente Mustersignale des identischen Zufallsprozesses mit bipolarer $(-1 \hspace{0.05cm} \rm V, +1 \hspace{0.05cm} \rm V)$ bzw. unipolarer $(0 \hspace{0.05cm} \rm V, 1 \hspace{0.05cm} \rm V)$ Signaldarstellung.
Hinweise:
- Die Aufgabe gehört zum Kapitel Kreuzkorrelationsfunktion_und_Kreuzleistungsdichte.
- Bezug genommen wird auch auf das Kapitel Autokorrelationsfunktion.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Skizzieren Sie die gesuchten Korrelationsfunktionen jeweils im Bereich von $-7T$ bis $7T$.
Fragebogen
Musterlösung
- $$\varphi_z ( \tau = 0) = {1}/{2} \cdot (1 {\rm V})^2 \hspace{0.15cm}\underline{= 0.5 {\rm V}^2}.$$
Für $\tau = \pm T$, $\underline{\tau = \pm 3T}$, ... ergibt sich $\varphi_z ( \tau)\hspace{0.15cm}\underline{ = 0}$.
Für die Zwischenwerte $\tau = \pm 2T$, $\tau = \pm 4T$, $\underline{\tau = \pm 6T}$, ... gilt:
- $$\varphi_z ( \tau) = \frac {1 {\rm V}^2}{2} \left(p \hspace{0.02cm} \cdot \hspace{0.02cm}p \hspace{0.2cm} + \hspace{0.2cm}p \hspace{0.02cm}\cdot \hspace{0.02cm}(p-1) \hspace{0.2cm}+\hspace{0.2cm} (p-1)\hspace{0.02cm} \cdot \hspace{0.02cm}p \hspace{0.2cm}+\hspace{0.2cm} (p-1)\hspace{0.02cm} \cdot \hspace{0.02cm}(p-1)\right) = \hspace{0.1cm}... \hspace{0.1cm}= 0.5\, {\rm V}^2 \cdot (1-2p)^2 .$$
Hierbei steht $p$ für $p \cdot (+1)$ und $(p-1)$ für $(1-p) \cdot (-1)$, also jeweils Wahrscheinlichkeit mal normierter Amplitudenwert. Mit $p = 0.25$ ergeben sich diese Zwischenwerte zu $\varphi_z ( \tau = \pm 6 T) \hspace{0.15cm}\underline{=0.125 \rm V^2}$.
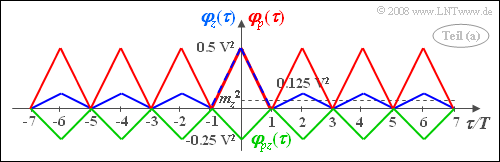
Die Skizze zeigt den Verlauf von $\varphi_z(\tau)$ für $p = 0.25$ im Bereich von $-7T \le \tau \le +7T$ als blaue Kurve.
- Aufgrund des rechteckförmigen Signalverlaufs ergibt sich eine Summe von Dreieckfunktionen.
- Für $p = 0.5$ würden die äußeren (kleineren) Dreiecke verschwinden.
(2) Die AKF $\varphi_p(\tau)$ des unipolaren periodischen Signals $p(t)$ ist in der allgemeingültigen Darstellung von (1) ⇒ AKF $\varphi_z(\tau)$ als Sonderfall für $p = 1$ enthalten. Man erhält nun eine periodische AKF (siehe roter Kurvenverlauf in obiger Skizze) mit
- $$\varphi_p ( \tau = 0) = \varphi_p ( \tau = \pm 2 T) = \varphi_p ( \tau = \pm 4 T) = \hspace{0.1cm} ... \hspace{0.1cm}\hspace{0.15cm}\underline{= 0.5 {\rm V}^2},$$
- $$\varphi_p ( \tau = \pm T) = \varphi_p ( \tau = \pm 3T) = \hspace{0.1cm} ... \hspace{0.1cm}\hspace{0.15cm}\underline{= 0}.$$
(3) Auch für die KKF ergibt sich für $\tau = \pm T$, $\underline{\tau = \pm 3T}$, ... , ... stets der Wert $0$. Dagegen sind die KKF-Werte für $\tau = \pm 2T$, $\tau = \pm 2T$, ... identisch mit denen bei $\tau = 0$:
- $$\varphi_{pz} ( \tau = 0) = \varphi_{pz} ( \tau = \pm 2 T) = \varphi_{pz} ( \tau = \pm 4 T) = \hspace{0.1cm} ... \hspace{0.1cm}= \frac {1 {\rm V}^2}{2} \left( p - (1-p)\right) = \frac {2p -1}{2}\, {\rm V}^2 .$$
Man erhält mit $p = 0.25$ folgende Ergebnisse (siehe grüne Kurve in obiger Skizze):
- $$\varphi_{pz} ( \tau = 0)\hspace{0.15cm}\underline{= -0.25 {\rm V}^2},\hspace{0.5cm} \varphi_{pz} ( \tau = 3T)\hspace{0.15cm}\underline{= 0},\hspace{0.5cm} \varphi_{pz} ( \tau = 6T)\hspace{0.15cm}\underline{= -0.25 {\rm V}^2}.$$
- Mit $p = 1$ würde dagegen $z(z) \equiv p(t)$gelten und damit natürlich auch $\varphi_{pz}(\tau) \equiv \varphi_{p}(\tau) \equiv \varphi_{z}(\tau)$.
- Für den Sonderfall $p = 0.5$ ergäbe sich keine Korrelation zwischen $p(t)$ und $z(t)$ und damit $\varphi_{pz}(\tau)=0$.
(4) Durch Einsetzen von $c(t) = a(t) + b(t)$ in die allgemeine AKF-Definition erhält man:
- $$\varphi_c ( \tau ) = \overline{c(t)\hspace{0.02cm} \cdot \hspace{0.02cm} c(t + \tau)} = \overline{a(t)\hspace{0.02cm} \cdot \hspace{0.02cm} a(t + \tau)} \hspace{0.1cm}+\hspace{0.1cm}\overline{a(t)\hspace{0.02cm} \cdot \hspace{0.02cm} b(t + \tau)} +\overline{b(t)\hspace{0.02cm} \cdot \hspace{0.02cm} a(t + \tau)} \hspace{0.1cm}+\hspace{0.1cm}\overline{b(t)\hspace{0.02cm} \cdot \hspace{0.02cm} b(t + \tau)}. $$
- $$\Rightarrow \hspace{0.5cm} \varphi_c ( \tau ) = \varphi_{a} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{ab} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{ba} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm}\varphi_{a} ( \tau ). $$
Richtig ist somit der Lösungsvorschlag 2.
- Der Lösungsvorschlag 1 trifft nur zu, wenn $a(t)$ und $b(t)$ unkorreliert sind.
- Der letzte Vorschlag, die Faltungsoperation, ist immer falsch. Eine ähnliche Gleichung würde sich nur dann ergeben, wenn wir die WDF $f_c(c)$ der Summe $c(t) = a(t) + b(t)$ betrachten und $a(t)$ und $b(t)$) statistisch unabhängig sind: $f_c (c) = f_a (a) \star f_b (b) .$
(5) Mit dem Ergebnis von (4) und unter Berücksichtigung des Faktors 1/2 erhält man:
- $$\varphi_s ( \tau ) = {1}/{4} \cdot \left[ \varphi_{p} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{z} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} 2 \cdot \varphi_{pz} ( \tau ) \right] . $$
Hierbei ist bereits berücksichtigt, dass die KKF zwischen $p(t)$ und $z(t)$ eine gerade Funktion ist, so dass auch $\varphi_{pz}(\tau) = \varphi_{zp}(\tau)$ gilt. Für $\tau = 0$ erhält man deshalb mit den obigen Ergebnissen allgemein:
- $$\varphi_s( \tau = 0) = {1}/{4} \cdot \left( 0.5 {\rm V}^2 +0.5 {\rm V}^2 + 2 \cdot \frac{2p-1}{2} {\rm V}^2\right) .$$
Mit $p = 0.25$ ergibt sich $ \varphi_{pz} ( \tau = 0 ) = 0.125\rm V^2$. Dieses Ergebnis ist plausibel. Im Mittel ist nur in jedem achten Intervall $s(t)=1 \hspace{0.05cm} \rm V$; ansonsten ist $s(t)=0 \hspace{0.05cm} \rm V$.
Für geradzahlige Vielfache von $T$ gilt:
- $$ \varphi_s ( \tau = \pm 2 T) = \varphi_s ( \tau = \pm 4 T) = \hspace{0.1cm} ... \hspace{0.1cm} = \frac {0.5 {\rm V}^2}{4} \left( (1-2p)^2 +1 + 2 \cdot (2p -1)\right) = 0.5 \, {\rm V}^2 \hspace{0.02cm} \cdot \hspace{0.02cm} p^2.$$
Mit $p = 0.5$ erhält man hierfür den Wert $0.03125 \hspace{0.1cm}V^2$. Alle AKF-Werte bei ungeradzahligen Vielfachen von $T$ sind wieder $0$. Damit ergibt sich der skizzierte AKF-Verlauf. Die gesuchten Zahlenwerte sind somit:
- $$\varphi_{s} ( \tau = 0)\hspace{0.15cm}\underline{= 0.125 {\rm V}^2},$$
- $$\varphi_{s} ( \tau = 3T)\hspace{0.15cm}\underline{= 0},$$
- $$\varphi_{s} ( \tau = 6T)\hspace{0.15cm}\underline{= -0.03125 {\rm V}^2}.$$
Ein Vergleich mit der Skizze zur Teilaufgabe (1) zeigt, dass das binäre Signal $s(t)$ bis auf den Faktor $1/4$ die gleiche AKF aufweist wie das Ternärsignal $z(t)$.