Aufgaben:Aufgabe 4.1Z: Verabredung zum Frühstück: Unterschied zwischen den Versionen
| Zeile 42: | Zeile 42: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Kommt Herr S. um 8 Uhr 30, so trifft er Frau M., wenn diese zwischen 8 Uhr 15 und 8 Uhr 45 ankommt. Damit ist die Wahrscheinlichkeit | |
| + | $$p_1 = \text{Pr(Herr S. trifft Frau M.)}\hspace{0.15cm}\underline{=50\%}.$$ | ||
| − | : | + | [[Datei:P_ID246__Sto_Z_4_1_d.png|right|Günstiger Bereich für Zusammentreffen]] |
| + | '''(2)''' Kommt Frau M. um 8 Uhr, so trifft sie Herrn S. nur dann, wenn dieser vor 8 Uhr 15 kommt. Erscheint Frau M. um 9 Uhr, dann muss Herr S. nach 8 Uhr 45 angekommen sein, damit sich beide treffen können. Die Wahrscheinlichkeit für ein Zusammentreffen ist in beiden Fällen: | ||
| + | $$p_1 = \text{Min[Pr(Herr S. trifft Frau M.)]}\hspace{0.15cm}\underline{=25\%}.$$ | ||
| − | + | '''(3)''' Von den beiden unter (2) berechneten Ankunftszeiten ist 9 Uhr ($\underline{\text{Minute = 60}}$) günstiger, da sie – falls Herr S. nicht da ist – sofort wieder gehen kann. | |
| − | |||
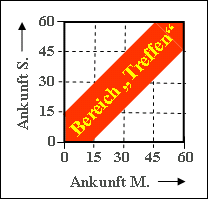
| − | + | '''(4)''' Die Wahrscheinlichkeit $p_4$ ergibt sich als das Verhältnis der roten Fläche in der Grafik zur Gesamtfläche $1$. Mit den Dreiecksflächen erhält man: | |
| − | + | $$p_{\rm d}=\rm 1-2\cdot\frac{1}{2}\cdot\frac{3}{4}\cdot\frac{3}{4}=\frac{7}{16}\hspace{0.15cm}\underline{=\rm 0.4375}.$$ | |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 17. März 2017, 18:06 Uhr
Frau M. und Herr S. treffen sich ja bekanntlich öfter einmal zu einem gemeinsamen Frühstück. Beide versprechen, an einem bestimmten Tag zwischen 8 Uhr und 9 Uhr zu einem solchen Treffen zu kommen. Weiter vereinbaren sie, dass jeder von ihnen in diesem Zeitraum (und nur in diesem) auf „Gut Glück” eintrifft und bis zu einer Viertelstunde auf den Anderen wartet.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Zufallsgrößen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Verwenden Sie bei den nachfolgenden Fragen als Zeitangabe die Minute der Ankunftszeit: „Minute = 0” steht für 8 Uhr, „Minute = 60” für 9 Uhr.
- Die Aufgabe entstand vor der Bundestagswahl 2002, als sowohl Angela Merkel als auch Edmund Stoiber Kanzlerkandidat(in) der CDU/CSU werden wollten. Bei einem gemeinsamen Frühstück in Wolfratshausen verzichtete Frau Merkel. Die spätere Wahl gewann Gerhard Schröder.
Fragebogen
Musterlösung
(2) Kommt Frau M. um 8 Uhr, so trifft sie Herrn S. nur dann, wenn dieser vor 8 Uhr 15 kommt. Erscheint Frau M. um 9 Uhr, dann muss Herr S. nach 8 Uhr 45 angekommen sein, damit sich beide treffen können. Die Wahrscheinlichkeit für ein Zusammentreffen ist in beiden Fällen: $$p_1 = \text{Min[Pr(Herr S. trifft Frau M.)]}\hspace{0.15cm}\underline{=25\%}.$$
(3) Von den beiden unter (2) berechneten Ankunftszeiten ist 9 Uhr ($\underline{\text{Minute = 60}}$) günstiger, da sie – falls Herr S. nicht da ist – sofort wieder gehen kann.
(4) Die Wahrscheinlichkeit $p_4$ ergibt sich als das Verhältnis der roten Fläche in der Grafik zur Gesamtfläche $1$. Mit den Dreiecksflächen erhält man: $$p_{\rm d}=\rm 1-2\cdot\frac{1}{2}\cdot\frac{3}{4}\cdot\frac{3}{4}=\frac{7}{16}\hspace{0.15cm}\underline{=\rm 0.4375}.$$