Aufgaben:Aufgabe 2.2: Gleichsignalanteile: Unterschied zwischen den Versionen
| Zeile 44: | Zeile 44: | ||
{Wie groß ist der Gleichanteil des Signals $x_3(t)$? | {Wie groß ist der Gleichanteil des Signals $x_3(t)$? | ||
|type="{}"} | |type="{}"} | ||
| − | $x_3(t)\hspace{-0.1cm}:\,\,A_0$ = { -0.35--0.31 } V | + | $x_3(t)\hspace{-0.1cm}:\,\,A_0$ = { -0.35--0.31 } ${\rm V}$ |
{Wie groß ist der Gleichanteil des Signals $x_4(t)$? | {Wie groß ist der Gleichanteil des Signals $x_4(t)$? | ||
|type="{}"} | |type="{}"} | ||
| − | $x_4(t)\hspace{-0.1cm}:\,\,A_0$ = { 0.5 3% } V | + | $x_4(t)\hspace{-0.1cm}:\,\,A_0$ = { 0.5 3% } ${\rm V}$ |
{Wie groß ist der Gleichanteil des Signals $x_6(t)$? | {Wie groß ist der Gleichanteil des Signals $x_6(t)$? | ||
|type="{}"} | |type="{}"} | ||
| − | $x_6(t)\hspace{-0.1cm}:\,\,A_0$ = { 0.5 3% } V | + | $x_6(t)\hspace{-0.1cm}:\,\,A_0$ = { 0.5 3% } ${\rm V}$ |
</quiz> | </quiz> | ||
Version vom 15. Januar 2017, 14:09 Uhr
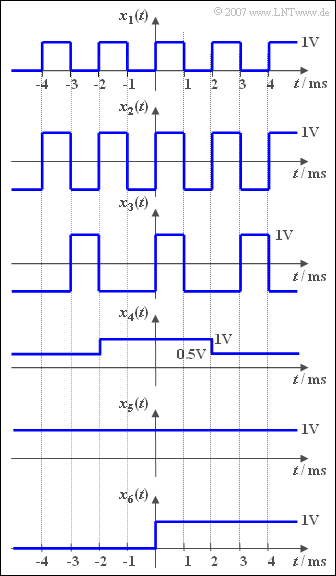
Die Grafik zeigt einige Zeitsignale, die für alle Zeiten (von $-\infty$ bis $+\infty$) definiert sind. Bei allen sechs Beispielsignalen $x_i(t)$ kann für die zugehörige Spektralfunktion geschrieben werden:
$$X_i(f)=A_0\cdot{\rm \delta}(f)+\Delta X_i(f).$$
Hierbei bezeichnen
- $A_0$ den Gleichsignalanteil, und
- $\Delta X_i(f)$ das Spektrum des um den Gleichanteil verminderten Restsignals $\Delta x_i(t) = x_i(t) - A_0$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Gleichsignal - Grenzfall eines periodischen Signals.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
2. Subtrahiert man vom Signal $x_5(t)$ den Gleichanteil $1\text{V}$, so ist das Restsignal $\Delta x_5(t) = x5(t) – 1\text{V}$ gleich Null. Dementspechend ist auch die Spektralfunktion $\Delta X_5(f) = 0$.
Bei allen anderen Zeitverläufen ist $\Delta x_i(t)$ ungleich $0$ und damit auch die dazugehörige Spektralfunktion $\Delta X_i(f)$ ⇒ Richtig ist allein der Lösungsvorschlag 5.
3. Bei einem periodischen Signal genügt zur Berechnung des Gleichsignalanteils $A_0$ die Mittelung über eine Periodendauer. Beim Beispielsignal $x_3(t)$ ist diese $T_0 = 3\,\text{ms}$. Damit ergibt sich der gesuchte Gleichanteil zu
$$A_0=\rm \frac{1}{3\,ms}\cdot [1\,V\cdot 1\,ms+(-1\,V)\cdot 2\,ms] \hspace{0.15cm}\underline{=-0.333\,V}.$$
4. Für das Signal $x_4(t)$ kann geschrieben werden: $x_4(t) = 0.5 \,{\rm V} + Δx_4(t)$. Hierbei bezeichnet $Δx_4(t)$ einen Rechteckimpuls der Amplitude $0.5 \,{\rm V} $ und der Dauer $4 \,{\rm ms} $, der aufgrund seiner endlichen Dauer nicht zum Gleichsignalanteil beiträgt. Deshalb gilt hier $A_0 \underline{=0.5 \,{\rm V}}$.
5. Die allgemeine Gleichung zur Berechnung des Gleichsignalanteils lautet:
$$A_0=\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int_{-T_{\rm M}/2}^{+T_{\rm M}/2}x(t)\, {\rm d }t.$$
Spaltet man dieses Integral in zwei Teilintegrale auf, so erhält man:
$$A_0=\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{-T_{\rm M}/2}^{0}0 {\rm V} \cdot\, {\rm d } {\it t }+\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{0}^{+T_{\rm M}/2}1 \rm V\cdot\, {\rm d }{\it t }.$$
Nur der zweite Term liefert einen Beitrag. Daraus folgt wiederum $A_0 \underline{=0.5 \,{\rm V}}$.