Digitalsignalübertragung/Lineare Nyquistentzerrung: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
|||
| (28 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
== Struktur des optimalen Nyquistentzerrers == | == Struktur des optimalen Nyquistentzerrers == | ||
<br> | <br> | ||
| − | In diesem Abschnitt gehen wir von folgendem Blockschaltbild eines Binärsystems aus. | + | In diesem Abschnitt gehen wir von folgendem Blockschaltbild eines Binärsystems aus. Hierzu ist anzumerken: |
| + | [[Datei:P ID1423 Dig T 3 5 S1 version1.png|right|frame|Blockschaltbild des optimalen Nyquistentzerrers|class=fit]] | ||
| − | + | *Die "Diracquelle" liefert die zu übertragende Nachricht in binärer bipolarer Form ⇒ Amplitudenkoeffizienten $a_\nu \in \{ -1, \hspace{0.05cm}+1\}$. Die Quelle wird als redundanzfrei vorausgesetzt.<br> | |
| − | + | *Die "Sendeimpulsform" $g_s(t)$ wird durch den Senderfrequenzgang $H_{\rm S}(f)$ berücksichtigt. Bei allen Beispielen ist $H_{\rm S}(f) = {\rm si}(\pi f T)$ zugrunde gelegt ⇒ NRZ–Rechteck–Sendeimpulse.<br> | |
| − | *Die | ||
| − | * | + | *Bei manchen Herleitungen werden Sender und Kanal durch den "gemeinsamen Frequenzgang" $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$ zusammengefasst.<br> |
| − | * | + | *Das Empfangsfilter $H_{\rm E}(f)$ setzt sich multiplikativ aus dem [[Stochastische_Signaltheorie/Matched-Filter|Matched–Filter]] $H_{\rm MF}(f) = H_{\rm SK}^\star(f)$ und dem [[Digitalsignalübertragung/Lineare_Nyquistentzerrung#Wirkungsweise_des_Transversalfilters|Transversalfilter]] $H_{\rm TF}(f)$ zusammen, zumindest kann es gedanklich so aufgespalten werden. |
| − | + | *Der Gesamtfrequenzgang zwischen Diracquelle und Schwellenwertentscheider soll die [[Digitalsignal%C3%BCbertragung/Eigenschaften_von_Nyquistsystemen#Erstes_Nyquistkriterium_im_Frequenzbereich|"erste Nyquistbedingung"]] erfüllen. Es muss also gelten: | |
| − | + | :$$H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) | |
| − | *Der Gesamtfrequenzgang zwischen | ||
| − | |||
| − | |||
= H_{\rm Nyq}(f) | = H_{\rm Nyq}(f) | ||
| − | \hspace{0.05cm}. | + | \hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | :: | + | *Mit dieser Bedingung gibt es keine Impulsinterferenzen und man erhält die maximale Augenöffnung. Deshalb gelten für das [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung#Optimaler_Bin.C3.A4rempf.C3.A4nger_-_Realisierung_mit_Matched-Filter|"Detektions–SNR"]] und den [[Digitalsignalübertragung/Optimierung_der_Basisbandübertragungssysteme#Systemoptimierung_bei_Spitzenwertbegrenzung|"Systemwirkungsgrad"]] bei binärer Signalisierung: |
| + | :$$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
\eta = \frac{\rho_d }{\rho_{d,\hspace{0.05cm} {\rm max}}} | \eta = \frac{\rho_d }{\rho_{d,\hspace{0.05cm} {\rm max}}} | ||
= \frac{\rho_d }{2 \cdot s_0^2 \cdot T/N_0} | = \frac{\rho_d }{2 \cdot s_0^2 \cdot T/N_0} | ||
= \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} | = \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} | ||
| − | \hspace{0.05cm}. | + | \hspace{0.05cm}.$$ |
| − | *Die Optimierungsaufgabe beschränkt sich also darauf, das Empfangsfilter | + | *Die Optimierungsaufgabe beschränkt sich also darauf, das Empfangsfilter $H_{\rm E}(f)$ so zu bestimmen, dass die normierte Rauschleistung vor dem Entscheider den kleinstmöglichen Wert annimmt: |
::<math>\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ | ::<math>\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ | ||
| Zeile 42: | Zeile 38: | ||
\,{\rm d} f \stackrel {!}{=} {\rm Minimum}\hspace{0.05cm}.</math> | \,{\rm d} f \stackrel {!}{=} {\rm Minimum}\hspace{0.05cm}.</math> | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ Wir bezeichnen die hier beschriebene Konfiguration als '''Optimale Nyquistentzerrung''' $\rm (ONE)$. }} | ||
| + | |||
| + | |||
| + | Obwohl diese auch – und besonders effektiv – bei Mehrstufensystemen anwendbar ist, setzen wir zunächst $M = 2$. | ||
| − | == Wirkungsweise des Transversalfilters | + | == Wirkungsweise des Transversalfilters== |
<br> | <br> | ||
| + | [[Datei:P ID1424 Dig T 3 5 S2 version2.png|right|frame|Transversalfilter (zweiter Ordnung) als Teil des optimalen Nyquistentzerrers|class=fit]] | ||
Verdeutlichen wir uns zunächst die Aufgabe des symmetrischen Transversalfilters | Verdeutlichen wir uns zunächst die Aufgabe des symmetrischen Transversalfilters | ||
| − | + | :$$H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ | |
| − | : | ||
\hspace{0.4cm} | \hspace{0.4cm} | ||
h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T) | h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T) | ||
| − | + | $$ | |
| + | |||
| + | mit folgenden Eigenschaften: | ||
| + | *$N$ gibt die "Ordnung" des Filters an ⇒ die Grafik zeigt ein Filter zweiter Ordnung $(N=2)$. | ||
| + | |||
| + | *Für die Filterkoeffizienten gilt $k_{-\lambda} = k_{\lambda}$ ⇒ symmetrische Struktur ⇒ $H_{\rm TF}(f)$ ist reell. | ||
| + | |||
| + | *$H_{\rm TF}(f)$ ist somit durch die Koeffizienten $k_0$, ... , $k_N$ vollständig bestimmt. | ||
| − | |||
| − | + | Für den Eingangsimpuls $g_m(t)$ setzen wir ohne Einschränkung der Allgemeingültigkeit voraus, dass dieser | |
| − | + | *symmetrisch um $t=0$ ist $($Ausgang des Matched–Filters$)$,<br> | |
| − | + | *zu den Zeiten $\nu \cdot T$ und $-\nu \cdot T$ jeweils den Wert $g_m(\nu)$ besitzt.<br> | |
| − | *zu den Zeiten | ||
| − | |||
| − | : | + | Damit lauten die Eingangsimpulswerte: |
| + | :$$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace | ||
{0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} | {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} | ||
| − | ... \hspace{0.05cm}.< | + | \text{...}\hspace{0.05cm}.$$ |
| + | |||
| + | Für den Detektionsgrundimpuls $g_d(t)$ am Filterausgang ergeben sich demzufolge zu den Zeitpunkten $\nu \cdot T$ mit den Abkürzungen $g_0 =g_d(t= 0)$, $g_1 =g_d(t= \pm T)$, $g_2 =g_d(t= \pm 2T)$ folgende Werte: | ||
| + | :$$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 | ||
| + | \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$ | ||
| + | :$$ t = \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot g_m(1) + k_1 | ||
| + | \cdot \big [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3) \big ], $$ | ||
| + | :$$ t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 | ||
| + | \cdot \big [g_m(1)+g_m(3)\big ]+ k_2 \cdot \big [g_m(2)+g_m(4)\big ] | ||
| + | \hspace{0.05cm}. $$ | ||
| + | |||
| + | Aus diesem System mit drei linear unabhängigen Gleichungen kann man nun die Filterkoeffizienten $k_0$, $k_1$ und $k_2$ so bestimmen, dass der Detektionsgrundimpuls $g_d(t)$ folgende Stützstellen aufweist: | ||
| + | :$$\text{...}\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 | ||
| + | ,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 | ||
| + | = 0 ,\hspace{0.25cm}g_3 ,\hspace{0.15cm} \text{...}$$ | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Wir gehen von dem symmetrischen Eingangssignal entsprechend dem oberen Diagramm in der Grafik aus. Mit der Abkürzung $g_m(\nu)= g_m(\pm \nu \cdot T)$ gibt es folgende Abtastwerte im Abstand der Symboldauer $T$: | ||
| + | :$$g_m(t) = {\rm e}^{ - \sqrt{2 \hspace{0.05cm} \cdot \hspace{0.05cm}\vert\hspace{0.05cm} t \hspace{0.05cm} \vert /T} }\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} g_m(0) = 1 ,\hspace{0.35cm}g_m(1)= | ||
| + | 0.243,\hspace{0.35cm}g_m(2)= 0.135,\hspace{0.35cm}g_m(3)= 0.086, | ||
| + | \hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$ | ||
| + | |||
| + | ⇒ Für den Ausgangsimpuls soll $g_d(t =0) = 1$ und $g_d(t =\pm T) = 0$ gelten. Hierzu eignet sich ein Laufzeitfilter erster Ordnung mit den Koeffizienten $k_0$ und $k_1$, die folgende Bedingungen erfüllen müssen: | ||
| + | [[Datei:P ID1425 Dig T 3 5 S2b version1.png|right|frame|Eingangs- und Ausgangsimpuls des optimalen Nyquistentzerrers]] | ||
| + | :$$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | ||
| + | \big [1.000 +0.135 \big ] = 0\hspace{0.3cm}\Rightarrow | ||
| + | \hspace{0.3cm}{k_1} = | ||
| + | -0.214 \cdot {k_0}\hspace{0.05cm},$$ | ||
| + | :$$ t = 0 \hspace{-0.1cm} : \hspace{0.6cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot | ||
| + | 0.243= 1\hspace{0.3cm}\Rightarrow \hspace{0.3cm}0.896 \cdot {k_0} | ||
| + | = 1 \hspace{0.05cm}.$$ | ||
| + | |||
| + | Daraus erhält man die optimalen Filterkoeffizienten $k_0 = 1.116$ und $k_1 = 0.239$. | ||
| + | *Das mittlere Diagramm zeigt, dass damit der erste Vorläufer und der erste Nachläufer kompensiert werden können und zugleich $g_d(0) =1$ gilt (gelbe Hinterlegung). | ||
| + | |||
| + | *Die weiteren Detektionsgrundimpulswerte (blaue Kreise) sind aber von Null verschieden und bewirken Impulsinterferenzen.<br> | ||
| + | |||
| + | |||
| + | ⇒ Das untere Diagramm zeigt, dass mit einem Filter zweiter Ordnung $(N = 2)$ Nulldurchgänge bei $\pm T$ und bei $\pm 2T$ erzwungen werden, wenn die Koeffizienten $k_0 = 1.127$, $k_1 = 0.219$ und $k_2 = 0.075$ geeignet gewählt sind. Das Gleichungssystem zur Bestimmung der optimalen Koeffizienten lautet dabei: | ||
| + | :$$t = 0\hspace{-0.1cm}:\hspace{0.85cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 | ||
| + | \cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$ | ||
| + | :$$t= \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | ||
| + | \big [1.000+0.135 \big ]+ k_2 \cdot \big [0.243+0.086 \big ] = 0\hspace{0.05cm},$$ | ||
| + | :$$t = \pm 2 T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot 0.135 + k_1 \cdot | ||
| + | \big [0.243+0.086\big ]+ k_2 \cdot \big [1.000 + 0.059 \big ]= 0 \hspace{0.05cm}.$$}}<br> | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Fazit:}$ Die Ergebnisse können wie folgt verallgemeinert werden: | ||
| + | #Mit einem Laufzeitfilter $N$–ter Ordnung kann der Hauptwert zu $g_d(0)=1$ (normiert) gemacht werden | ||
| + | # Außerdem können die ersten $N$ Nachläufer $g_{\nu}$ und die ersten $N$ Vorläufer $g_{-\nu}$ zu Null gemacht werden.<br> | ||
| + | #Weitere Vor– und Nachläufer $(\nu \gt N)$ lassen sich so nicht kompensieren. | ||
| + | #Es ist sogar möglich, dass die Vor– und Nachläufer außerhalb des Kompensationsbereichs vergrößert werden oder sogar neu entstehen.<br> | ||
| + | #Im Grenzübergang $N \to \infty$ (in der Praxis heißt das: ein Filter mit sehr vielen Koeffizienten) ist eine vollständige Nyquistentzerrung und damit eine impulsinterferenzfreie Übertragung möglich.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Beschreibung im Frequenzbereich == | |
| + | <br> | ||
| + | Die Tatsache, dass sich der optimale Nyquistentzerrer multiplikativ aus | ||
| + | *dem Matched–Filter $H_{\rm MF}(f) = H_{\rm S}^\star (f)\cdot H_{\rm K}^\star(f)$ – also angepasst an den Empfangsgrundimpuls $g_r(t)$ – und<br> | ||
| + | *einem Transversalfilter $H_{\rm MF}(f)$ mit unendlich vielen Filterkoeffizienten<br><br> | ||
| − | :< | + | zusammensetzt, folgt aus dem ersten Nyquistkriterium. Durch Anwendung der [https://de.wikipedia.org/wiki/Variationsrechnung "Variationsrechnung"] erhält man den Frequenzgang des Transversalfilters – siehe [ST85]<ref name='ST85'> Söder, G.; Tröndle, K.: "Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme." Berlin – Heidelberg: Springer, 1985.</ref>: |
| − | ,\hspace{0. | + | [[Datei:Dig_T_3_5_S3b_version2.png|right|frame|(Betrags–) Frequenzgang des Transversalfilter (links) und des gesamten optimalen Nyquistentzerrers (rechts)|class=fit]] |
| − | = 0 | + | $$H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - |
| + | \frac{\kappa}{T}) | ||
| + | |^2},$$ | ||
| + | $$\text{wobei }H_{\rm SK}(f) = H_{\rm S}(f)\cdot H_{\rm K}(f).$$ | ||
| + | |||
| + | Die linke Grafik zeigt $20 \cdot \lg \ H_{\rm TF}(f)$ im Bereich $| f | \le 1/T$. Vorausgesetzt sind rechteckförmige NRZ–Sendeimpulse und ein Koaxialkabel mit der charakteristischen Kabeldämpfung $a_\star$. | ||
| + | |||
| + | Man erkennt aus obiger Gleichung und Grafik: | ||
| + | *$H_{\rm TF}(f)$ ist reell ⇒ symmetrische Transversalfilterstruktur ⇒ $k_{-\lambda} =k_{+\lambda} $.<br> | ||
| + | |||
| + | *$H_{\rm TF}(f)$ ist gleichzeitig eine mit der Frequenz $1/T$ periodische Funktion ⇒ Koeffizienten des Filters ergeben sich aus der [[Signaldarstellung/Fourierreihe|"Fourierreihe"]] (angewandt auf die Spektralfunktion): | ||
| + | :$$k_\lambda =T \cdot \int_{-1/(2T)}^{+1/(2T)}\frac{\cos(2 \pi f \lambda T)} {\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | ||
| + | {\kappa}/{T}) | ||
| + | |^2} \hspace{0.2cm} {\rm d} f$$ | ||
| + | :$$ \hspace{0.25cm}\Rightarrow \hspace{0.25cm}H_{\rm TF}(f) = | ||
| + | \sum\limits_{\lambda = -\infty}^{+\infty} k_\lambda \cdot {\rm | ||
| + | e}^{-{\rm j}2 \pi f \lambda T}\hspace{0.05cm}.$$ | ||
| + | |||
| + | In der rechten Grafik ist der Frequenzgang $20 \cdot \lg \ |H_{\rm E}(f)|$ des gesamten Empfangsfilters einschließlich Matched–Filter dargestellt. Es gilt: | ||
| + | |||
| + | :$$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{\star}(f)}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | ||
| + | {\kappa}/{T}) | ||
| + | |^2}.$$ | ||
| + | |||
| + | Zu diesen Darstellungen ist anzumerken: | ||
| + | *Für $a_\star = 0 \ \rm dB$ (idealer Kanal, grüne Null–Linie) kann auf das Transversalfilter $H_{\rm TF}(f)$ verzichtet werden und es gilt für NRZ–Rechteckimpulse, wie bereits im Abschnitt [[Digitalsignal%C3%BCbertragung/Fehlerwahrscheinlichkeit_bei_Basisband%C3%BCbertragung#Optimaler_Bin.C3.A4rempf.C3.A4nger_-_Realisierung_mit_Matched-Filter|"Optimaler Binärempfänger – Realisierung mit Matched-Filter"]] hergeleitet: | ||
| + | :$$H_{\rm E}(f) =H_{\rm S}(f) = {\rm si} (\pi f T).$$ | ||
| + | *Während der Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ bei $a_\star \ne 0 \ \rm dB$ symmetrisch zur Nyquistfrequenz $f_{\rm Nyq} = 1/(2T)$ ist, ist diese Symmetrie beim Empfangsfilter–Gesamtfrequenzgang $H_{\rm E}(f)$ nicht mehr gegeben.<br> | ||
| + | |||
| + | *Die Maxima der Frequenzgänge $H_{\rm TF}(f)$ und $|H_{\rm E}(f)|$ hängen signifikant von der charakteristischen Kabeldämpfung $a_\star$ ab. Aus dem blauen bzw. roten Funktionsverlauf kann abgelesen werden: | ||
| + | :$$a_{\star} = 40\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm | ||
| + | TF}(f)\big]\hspace{0.1cm} \approx 80\,{\rm dB}, \hspace{0.2cm}{\rm | ||
| + | Max}\big[\ |H_{\rm E}(f)| \ \big] \approx 40\,{\rm dB}\hspace{0.05cm},$$ | ||
| + | :$$a_{\star} = 80\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big] | ||
| + | \approx 160\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)|\ \big] | ||
| + | \approx 80\,{\rm dB}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | == Approximation des optimalen Nyquistentzerrers == | ||
| + | <br> | ||
| + | Wir betrachten nun den Gesamtfrequenzgang zwischen Diracquelle und Entscheider: | ||
| + | *Dieser setzt sich multiplikativ aus den Frequenzgängen von Sender, Kanal und Empfänger zusammen. | ||
| + | |||
| + | *Entsprechend der Herleitung muss der Gesamtfrequenzgang die Nyquistbedingung erfüllen: | ||
| + | [[Datei:P ID1428 Dig T 3 5 S3c version1.png|right|frame|Optimaler Nyquistfrequenzgang (Übertragungssystem mit Koaxialkabel)|class=fit]] | ||
| + | |||
| + | :$$H_{\rm Nyq}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f) = | ||
| + | \frac{|H_{\rm SK}(f)|^2}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | ||
| + | {\kappa}/{T}) | ||
| + | |^2}\hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Grafik zeigt folgende Eigenschaften des '''optimalen Nyquistentzerrers''' $\rm (ONE)$: | ||
| + | *Ist die Kabeldämpfung hinreichend groß $(a_\star \ge 10 \ \rm dB)$, so kann man den Gesamtfrequenzgang mit guter Näherung durch den [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen#1.2FT.E2.80.93Nyquistspektren|"Cosinus–Rolloff–Tiefpass"]] beschreiben.<br> | ||
| + | |||
| + | *Je größer $a_\star$ ist, desto kleiner ist der Rolloff–Faktor $r$ und um so steiler verläuft der Flankenabfall. Für die charakteristische Kabeldämpfung $a_\star = 40 \ \rm dB$ (blaue Kurve) ergibt sich $r \approx 0.4$, für $a_\star = 80 \ \rm dB$ (rote Kurve) $r \approx 0.18$.<br> | ||
| + | |||
| + | *Oberhalb der Frequenz $f_{\rm Nyq} \cdot (1 + r)$ besitzt $H_{\rm Nyq}(f)$ keine Anteile. Bei idealem Kanal ⇒ $a_\star = 0 \ \rm dB$ (grüne Kurve) reicht $H_{\rm Nyq}(f)= {\rm si}^2(\pi f T)$ allerdings theoretisch bis ins Unendliche. | ||
| + | |||
| + | |||
| + | ⇒ Das interaktive HTML5/JavaScript–Applet [[Applets:Frequenzgang_und_Impulsantwort|"Frequenzgang und Impulsantwort"]] verdeutlicht unter anderem die Eigenschaften des Cosinus–Rolloff–Tiefpasses. | ||
| + | |||
| + | |||
| + | == Berechnung der normierten Störleistung == | ||
| + | <br> | ||
| + | Wir betrachten nun noch die (normierte) Störleistung am Entscheider. Für diese gilt: | ||
| + | |||
| + | :$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ | ||
| + | (2T)} =T \cdot \int_{-1/(2T)}^{+1/(2T)} |H_{\rm E}(f)|^2 | ||
| + | \,{\rm d} f .$$ | ||
| + | |||
| + | [[Datei:P ID1429 Dig T 3 5 S5 version1.png|right|frame|Zur Berechnung der normierten Störleistung beim optimalen Nyquistentzerrer $\rm (ONE)$|class=fit]] | ||
| + | *Das linke Diagramm der Grafik zeigt $|H_{\rm E}(f)|^2$ im linearen Maßstab für die charakteristische Kabeldämpfung $a_\star = 80 \ \rm dB$. Beachten Sie, dass $|H_{\rm E}(f = 0)|^2 = 1$ ist. | ||
| + | |||
| + | *Da die Frequenz in dieser Darstellung auf $1/T$ normiert wurde, entspricht die normierte Störleistung genau der (rot hinterlegten) Fläche unter dieser Kurve. Die numerische Auswertung ergibt: | ||
| + | |||
| + | :$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = 1.68 \cdot 10^7\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm | ||
| + | lg}\hspace{0.1cm}\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 \approx | ||
| + | 72.25\,{\rm dB} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Es kann gezeigt werden, dass die normierte Störleistung allein mit dem Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ berechnet werden kann, wie in der rechten Grafik dargestellt: | ||
| + | :$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot | ||
| + | \int_{-1/(2T)}^{+1/(2T)} H_{\rm TF}(f) \,{\rm d} f | ||
| + | \hspace{0.3cm}(= k_0)\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Die roten Flächen sind in beiden Bildern exakt gleich. | ||
| + | <br clear=all> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ Die normierten Störleistung des optimalen Nyquistentzerrers ist gleich dem Fourierkoeffizienten $k_0$, wenn man den reellen, symmetrischen und periodischen Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ als Fourierreihe darstellt. | ||
| + | |||
| + | [[Datei:P ID1430 Dig T 3 5 S5b version3.png|right|frame|Koeffizienten des optimalen Nyquistentzerrers $\rm (ONE)$|class=fit]] | ||
| + | *In der zweiten Spalte der Tabelle ist $10 \cdot \lg \ (k_0)$ abhängig von der charakteristischen Kabeldämpfung $a_\star$ eines Koaxialkabels angegeben. | ||
| + | |||
| + | *Aufgrund der gewählten Normierung gilt die Tabelle auch für [[Digitalsignalübertragung/Impulsinterferenzen_bei_mehrstufiger_Übertragung#Augen.C3.B6ffnung_bei_redundanzfreien_Mehrstufensystemen|"redundanzfreie Mehrstufensysteme"]]; hierbei bezeichnet $M$ die Stufenzahl.<br> | ||
| + | |||
| + | *Die Koeffizienten $k_1$, $k_2$, $k_3$, ... des Transversalfilters weisen für $a_\star \ne 0 \ \rm dB$ alternierende Vorzeichen auf. | ||
| + | |||
| + | *Für $a_\star = 40 \ \rm dB$ sind vier Koeffizienten betragsmäßig größer als $k_0/10$, für $a_\star = 80 \ \rm dB$ sogar sieben.}} | ||
| + | |||
| + | == Vergleich anhand des Systemwirkungsgrades == | ||
| + | <br> | ||
| + | Für einen Systemvergleich eignet sich der [[Digitalsignalübertragung/Optimierung_der_Basisbandübertragungssysteme#Systemoptimierung_bei_Leistungsbegrenzung|"Systemwirkungsgrad"]], der das erreichbare Detektions–SNR $\rho_d$ in Bezug zum maximalen SNR $\rho_{d, \ {\rm max}}$ setzt, das allerdings nur bei idealem Kanal $H_{\rm K}(f) \equiv 1$ erreichbar ist. | ||
| + | [[Datei:P ID1431 Dig T 3 5 S6 version1.png|right|frame|Vergleich binärer und mehrstufiger Ünertragungssysteme gemäß $\text{GTP}$ bzw. $\text{ONE}$|class=fit]] | ||
| + | Für den Systemwirkungsgrad gilt bei $M$–stufiger Übertragung und optimaler Nyquistentzerrung: | ||
| + | :$$\eta = \frac{\rho_d}{s_0^2 \cdot T / N_0}=\frac{{\rm log_2}\hspace{0.1cm}M}{(M-1)^2 \cdot k_0}.$$ | ||
| + | |||
| + | *Die (normierte) Störleistung $k_0$ kann aus der [[Digitalsignal%C3%BCbertragung/Lineare_Nyquistentzerrung#Berechnung_der_normierten_St.C3.B6rleistung| '''Tabelle''']] auf der letzten Seite abgelesen werden. | ||
| + | |||
| + | * Beachten Sie die Normierung der charakteristischen Kabeldämpfung $a_\star$ in der ersten Spalte. | ||
| + | |||
| + | *Die Tabelle aus [ST85]<ref name='ST85'/> ermöglicht einen Systemvergleich für die charakteristische Kabeldämpfung $a_\star = 80 \ \rm dB$. | ||
| + | |||
| + | |||
| + | Verglichen werden: | ||
| + | |||
| + | * der [[Digitalsignalübertragung/Berücksichtigung_von_Kanalverzerrungen_und_Entzerrung|"gaußförmige Gesamtfrequenzgang"]] $\text{(GTP)}$, der auch bei Optimierung zu einem impulsinterferenzbehafteten System führt, <br> | ||
| + | |||
| + | *der [[Digitalsignalübertragung/Lineare_Nyquistentzerrung#Struktur_des_optimalen_Nyquistentzerrers|"optimale Nyquistentzerrer"]] $\text{(ONE)}$, mit dem Impulsinterferenzen per se ausgeschlossen werden. | ||
| + | <br clear=all> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ Die Ergebnisse dieses Systemvergleichs können wie folgt zusammengefasst werden: | ||
| + | #Im binären Fall $(M = 2)$ ist das impulsinterferenzfreie System $\text{(ONE)}$ um etwa $6 \ \rm dB$ besser als das impulsinterferenzbehaftete System $\text{(GTP)}$.<br> | ||
| + | #Wendet man die optimale Nyquistentzerrung bei Mehrstufensystemen an, so ist gegenüber $\text{GTP}$ ein weiterer, deutlicher Störabstandsgewinn möglich. | ||
| + | #Für $M =4$ beträgt dieser Gewinn etwa $18.2 \ \rm dB$.<br> | ||
| + | #Das schmalbandige $\text{GTP}$–System kann allerdings deutlich verbessert werden, wenn man einen Empfänger mit Entscheidungsrückkopplung verwendet. | ||
| + | #Dieser wird im nächsten Kapitel behandelt.}}<br> | ||
| + | |||
| + | ⇒ Wir verweisen an dieser Stelle auf das interaktive SWF–Applet [[Applets:Lineare_Nyquistentzerrung|"Lineare Nyquistentzerrung"]]. | ||
| + | |||
| + | |||
| + | |||
| + | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:3.6_Transversalfilter_des_Optimalen_Nyquistentzerrers| Aufgabe 3.6: Transversalfilter des Optimalen Nyquistentzerrers]] | ||
| + | |||
| + | [[Aufgaben:3.6Z_Optimaler_Nyquistentzerrer_für_Exponentialimpuls| Aufgabe 3.6Z: Optimaler Nyquistentzerrer für Exponentialimpuls]] | ||
| + | |||
| + | [[Aufgaben:3.7_Nochmals_Optimale_Nyquistentzerrung|Aufgabe 3.7: Nochmals Optimale Nyquistentzerrung]] | ||
| − | + | [[Aufgaben:3.7Z_Regeneratorfeldlänge|Aufgabe 3.7Z: Regeneratorfeldlänge]] | |
| + | ==Quellenverzeichnis== | ||
| + | <references/> | ||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 22. Juni 2022, 14:09 Uhr
Inhaltsverzeichnis
Struktur des optimalen Nyquistentzerrers
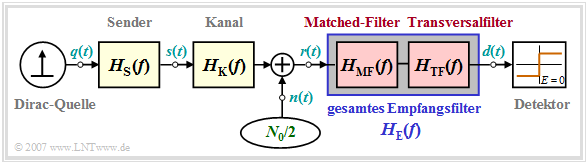
In diesem Abschnitt gehen wir von folgendem Blockschaltbild eines Binärsystems aus. Hierzu ist anzumerken:
- Die "Diracquelle" liefert die zu übertragende Nachricht in binärer bipolarer Form ⇒ Amplitudenkoeffizienten $a_\nu \in \{ -1, \hspace{0.05cm}+1\}$. Die Quelle wird als redundanzfrei vorausgesetzt.
- Die "Sendeimpulsform" $g_s(t)$ wird durch den Senderfrequenzgang $H_{\rm S}(f)$ berücksichtigt. Bei allen Beispielen ist $H_{\rm S}(f) = {\rm si}(\pi f T)$ zugrunde gelegt ⇒ NRZ–Rechteck–Sendeimpulse.
- Bei manchen Herleitungen werden Sender und Kanal durch den "gemeinsamen Frequenzgang" $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$ zusammengefasst.
- Das Empfangsfilter $H_{\rm E}(f)$ setzt sich multiplikativ aus dem Matched–Filter $H_{\rm MF}(f) = H_{\rm SK}^\star(f)$ und dem Transversalfilter $H_{\rm TF}(f)$ zusammen, zumindest kann es gedanklich so aufgespalten werden.
- Der Gesamtfrequenzgang zwischen Diracquelle und Schwellenwertentscheider soll die "erste Nyquistbedingung" erfüllen. Es muss also gelten:
- $$H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) = H_{\rm Nyq}(f) \hspace{0.05cm}.$$
- Mit dieser Bedingung gibt es keine Impulsinterferenzen und man erhält die maximale Augenöffnung. Deshalb gelten für das "Detektions–SNR" und den "Systemwirkungsgrad" bei binärer Signalisierung:
- $$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta = \frac{\rho_d }{\rho_{d,\hspace{0.05cm} {\rm max}}} = \frac{\rho_d }{2 \cdot s_0^2 \cdot T/N_0} = \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.05cm}.$$
- Die Optimierungsaufgabe beschränkt sich also darauf, das Empfangsfilter $H_{\rm E}(f)$ so zu bestimmen, dass die normierte Rauschleistung vor dem Entscheider den kleinstmöglichen Wert annimmt:
- \[\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ T} =T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f \stackrel {!}{=} {\rm Minimum}\hspace{0.05cm}.\]
$\text{Definition:}$ Wir bezeichnen die hier beschriebene Konfiguration als Optimale Nyquistentzerrung $\rm (ONE)$.
Obwohl diese auch – und besonders effektiv – bei Mehrstufensystemen anwendbar ist, setzen wir zunächst $M = 2$.
Wirkungsweise des Transversalfilters
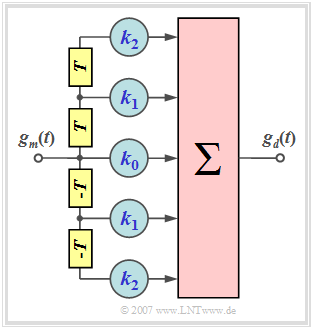
Verdeutlichen wir uns zunächst die Aufgabe des symmetrischen Transversalfilters
- $$H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T) $$
mit folgenden Eigenschaften:
- $N$ gibt die "Ordnung" des Filters an ⇒ die Grafik zeigt ein Filter zweiter Ordnung $(N=2)$.
- Für die Filterkoeffizienten gilt $k_{-\lambda} = k_{\lambda}$ ⇒ symmetrische Struktur ⇒ $H_{\rm TF}(f)$ ist reell.
- $H_{\rm TF}(f)$ ist somit durch die Koeffizienten $k_0$, ... , $k_N$ vollständig bestimmt.
Für den Eingangsimpuls $g_m(t)$ setzen wir ohne Einschränkung der Allgemeingültigkeit voraus, dass dieser
- symmetrisch um $t=0$ ist $($Ausgang des Matched–Filters$)$,
- zu den Zeiten $\nu \cdot T$ und $-\nu \cdot T$ jeweils den Wert $g_m(\nu)$ besitzt.
Damit lauten die Eingangsimpulswerte:
- $$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} \text{...}\hspace{0.05cm}.$$
Für den Detektionsgrundimpuls $g_d(t)$ am Filterausgang ergeben sich demzufolge zu den Zeitpunkten $\nu \cdot T$ mit den Abkürzungen $g_0 =g_d(t= 0)$, $g_1 =g_d(t= \pm T)$, $g_2 =g_d(t= \pm 2T)$ folgende Werte:
- $$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$
- $$ t = \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot g_m(1) + k_1 \cdot \big [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3) \big ], $$
- $$ t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 \cdot \big [g_m(1)+g_m(3)\big ]+ k_2 \cdot \big [g_m(2)+g_m(4)\big ] \hspace{0.05cm}. $$
Aus diesem System mit drei linear unabhängigen Gleichungen kann man nun die Filterkoeffizienten $k_0$, $k_1$ und $k_2$ so bestimmen, dass der Detektionsgrundimpuls $g_d(t)$ folgende Stützstellen aufweist:
- $$\text{...}\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 = 0 ,\hspace{0.25cm}g_3 ,\hspace{0.15cm} \text{...}$$
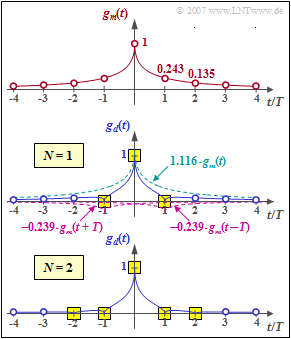
$\text{Beispiel 1:}$ Wir gehen von dem symmetrischen Eingangssignal entsprechend dem oberen Diagramm in der Grafik aus. Mit der Abkürzung $g_m(\nu)= g_m(\pm \nu \cdot T)$ gibt es folgende Abtastwerte im Abstand der Symboldauer $T$:
- $$g_m(t) = {\rm e}^{ - \sqrt{2 \hspace{0.05cm} \cdot \hspace{0.05cm}\vert\hspace{0.05cm} t \hspace{0.05cm} \vert /T} }\hspace{0.3cm} \Rightarrow \hspace{0.3cm} g_m(0) = 1 ,\hspace{0.35cm}g_m(1)= 0.243,\hspace{0.35cm}g_m(2)= 0.135,\hspace{0.35cm}g_m(3)= 0.086, \hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$
⇒ Für den Ausgangsimpuls soll $g_d(t =0) = 1$ und $g_d(t =\pm T) = 0$ gelten. Hierzu eignet sich ein Laufzeitfilter erster Ordnung mit den Koeffizienten $k_0$ und $k_1$, die folgende Bedingungen erfüllen müssen:
- $$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot \big [1.000 +0.135 \big ] = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{k_1} = -0.214 \cdot {k_0}\hspace{0.05cm},$$
- $$ t = 0 \hspace{-0.1cm} : \hspace{0.6cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot 0.243= 1\hspace{0.3cm}\Rightarrow \hspace{0.3cm}0.896 \cdot {k_0} = 1 \hspace{0.05cm}.$$
Daraus erhält man die optimalen Filterkoeffizienten $k_0 = 1.116$ und $k_1 = 0.239$.
- Das mittlere Diagramm zeigt, dass damit der erste Vorläufer und der erste Nachläufer kompensiert werden können und zugleich $g_d(0) =1$ gilt (gelbe Hinterlegung).
- Die weiteren Detektionsgrundimpulswerte (blaue Kreise) sind aber von Null verschieden und bewirken Impulsinterferenzen.
⇒ Das untere Diagramm zeigt, dass mit einem Filter zweiter Ordnung $(N = 2)$ Nulldurchgänge bei $\pm T$ und bei $\pm 2T$ erzwungen werden, wenn die Koeffizienten $k_0 = 1.127$, $k_1 = 0.219$ und $k_2 = 0.075$ geeignet gewählt sind. Das Gleichungssystem zur Bestimmung der optimalen Koeffizienten lautet dabei:
- $$t = 0\hspace{-0.1cm}:\hspace{0.85cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$
- $$t= \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot \big [1.000+0.135 \big ]+ k_2 \cdot \big [0.243+0.086 \big ] = 0\hspace{0.05cm},$$
- $$t = \pm 2 T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot 0.135 + k_1 \cdot \big [0.243+0.086\big ]+ k_2 \cdot \big [1.000 + 0.059 \big ]= 0 \hspace{0.05cm}.$$
$\text{Fazit:}$ Die Ergebnisse können wie folgt verallgemeinert werden:
- Mit einem Laufzeitfilter $N$–ter Ordnung kann der Hauptwert zu $g_d(0)=1$ (normiert) gemacht werden
- Außerdem können die ersten $N$ Nachläufer $g_{\nu}$ und die ersten $N$ Vorläufer $g_{-\nu}$ zu Null gemacht werden.
- Weitere Vor– und Nachläufer $(\nu \gt N)$ lassen sich so nicht kompensieren.
- Es ist sogar möglich, dass die Vor– und Nachläufer außerhalb des Kompensationsbereichs vergrößert werden oder sogar neu entstehen.
- Im Grenzübergang $N \to \infty$ (in der Praxis heißt das: ein Filter mit sehr vielen Koeffizienten) ist eine vollständige Nyquistentzerrung und damit eine impulsinterferenzfreie Übertragung möglich.
Beschreibung im Frequenzbereich
Die Tatsache, dass sich der optimale Nyquistentzerrer multiplikativ aus
- dem Matched–Filter $H_{\rm MF}(f) = H_{\rm S}^\star (f)\cdot H_{\rm K}^\star(f)$ – also angepasst an den Empfangsgrundimpuls $g_r(t)$ – und
- einem Transversalfilter $H_{\rm MF}(f)$ mit unendlich vielen Filterkoeffizienten
zusammensetzt, folgt aus dem ersten Nyquistkriterium. Durch Anwendung der "Variationsrechnung" erhält man den Frequenzgang des Transversalfilters – siehe [ST85][1]:
$$H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - \frac{\kappa}{T}) |^2},$$ $$\text{wobei }H_{\rm SK}(f) = H_{\rm S}(f)\cdot H_{\rm K}(f).$$
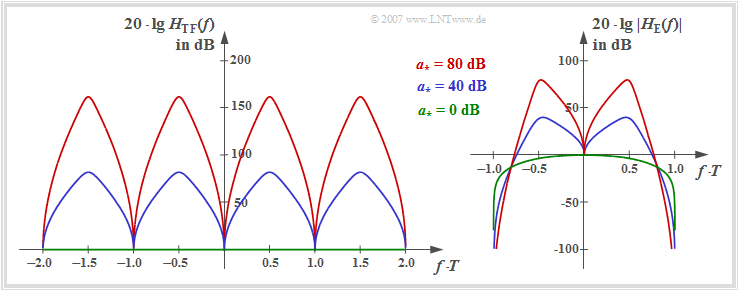
Die linke Grafik zeigt $20 \cdot \lg \ H_{\rm TF}(f)$ im Bereich $| f | \le 1/T$. Vorausgesetzt sind rechteckförmige NRZ–Sendeimpulse und ein Koaxialkabel mit der charakteristischen Kabeldämpfung $a_\star$.
Man erkennt aus obiger Gleichung und Grafik:
- $H_{\rm TF}(f)$ ist reell ⇒ symmetrische Transversalfilterstruktur ⇒ $k_{-\lambda} =k_{+\lambda} $.
- $H_{\rm TF}(f)$ ist gleichzeitig eine mit der Frequenz $1/T$ periodische Funktion ⇒ Koeffizienten des Filters ergeben sich aus der "Fourierreihe" (angewandt auf die Spektralfunktion):
- $$k_\lambda =T \cdot \int_{-1/(2T)}^{+1/(2T)}\frac{\cos(2 \pi f \lambda T)} {\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2} \hspace{0.2cm} {\rm d} f$$
- $$ \hspace{0.25cm}\Rightarrow \hspace{0.25cm}H_{\rm TF}(f) = \sum\limits_{\lambda = -\infty}^{+\infty} k_\lambda \cdot {\rm e}^{-{\rm j}2 \pi f \lambda T}\hspace{0.05cm}.$$
In der rechten Grafik ist der Frequenzgang $20 \cdot \lg \ |H_{\rm E}(f)|$ des gesamten Empfangsfilters einschließlich Matched–Filter dargestellt. Es gilt:
- $$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{\star}(f)}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}.$$
Zu diesen Darstellungen ist anzumerken:
- Für $a_\star = 0 \ \rm dB$ (idealer Kanal, grüne Null–Linie) kann auf das Transversalfilter $H_{\rm TF}(f)$ verzichtet werden und es gilt für NRZ–Rechteckimpulse, wie bereits im Abschnitt "Optimaler Binärempfänger – Realisierung mit Matched-Filter" hergeleitet:
- $$H_{\rm E}(f) =H_{\rm S}(f) = {\rm si} (\pi f T).$$
- Während der Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ bei $a_\star \ne 0 \ \rm dB$ symmetrisch zur Nyquistfrequenz $f_{\rm Nyq} = 1/(2T)$ ist, ist diese Symmetrie beim Empfangsfilter–Gesamtfrequenzgang $H_{\rm E}(f)$ nicht mehr gegeben.
- Die Maxima der Frequenzgänge $H_{\rm TF}(f)$ und $|H_{\rm E}(f)|$ hängen signifikant von der charakteristischen Kabeldämpfung $a_\star$ ab. Aus dem blauen bzw. roten Funktionsverlauf kann abgelesen werden:
- $$a_{\star} = 40\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big]\hspace{0.1cm} \approx 80\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)| \ \big] \approx 40\,{\rm dB}\hspace{0.05cm},$$
- $$a_{\star} = 80\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big] \approx 160\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)|\ \big] \approx 80\,{\rm dB}\hspace{0.05cm}.$$
Approximation des optimalen Nyquistentzerrers
Wir betrachten nun den Gesamtfrequenzgang zwischen Diracquelle und Entscheider:
- Dieser setzt sich multiplikativ aus den Frequenzgängen von Sender, Kanal und Empfänger zusammen.
- Entsprechend der Herleitung muss der Gesamtfrequenzgang die Nyquistbedingung erfüllen:
- $$H_{\rm Nyq}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f) = \frac{|H_{\rm SK}(f)|^2}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}\hspace{0.05cm}.$$
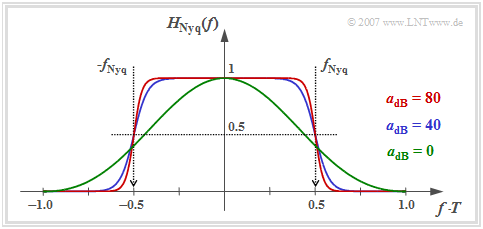
Die Grafik zeigt folgende Eigenschaften des optimalen Nyquistentzerrers $\rm (ONE)$:
- Ist die Kabeldämpfung hinreichend groß $(a_\star \ge 10 \ \rm dB)$, so kann man den Gesamtfrequenzgang mit guter Näherung durch den "Cosinus–Rolloff–Tiefpass" beschreiben.
- Je größer $a_\star$ ist, desto kleiner ist der Rolloff–Faktor $r$ und um so steiler verläuft der Flankenabfall. Für die charakteristische Kabeldämpfung $a_\star = 40 \ \rm dB$ (blaue Kurve) ergibt sich $r \approx 0.4$, für $a_\star = 80 \ \rm dB$ (rote Kurve) $r \approx 0.18$.
- Oberhalb der Frequenz $f_{\rm Nyq} \cdot (1 + r)$ besitzt $H_{\rm Nyq}(f)$ keine Anteile. Bei idealem Kanal ⇒ $a_\star = 0 \ \rm dB$ (grüne Kurve) reicht $H_{\rm Nyq}(f)= {\rm si}^2(\pi f T)$ allerdings theoretisch bis ins Unendliche.
⇒ Das interaktive HTML5/JavaScript–Applet "Frequenzgang und Impulsantwort" verdeutlicht unter anderem die Eigenschaften des Cosinus–Rolloff–Tiefpasses.
Berechnung der normierten Störleistung
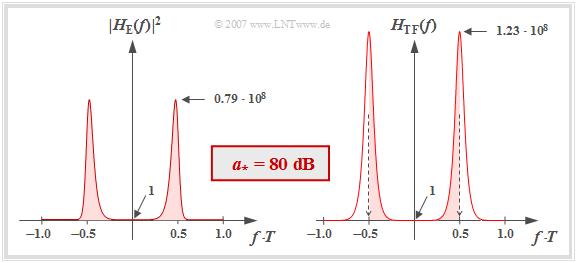
Wir betrachten nun noch die (normierte) Störleistung am Entscheider. Für diese gilt:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ (2T)} =T \cdot \int_{-1/(2T)}^{+1/(2T)} |H_{\rm E}(f)|^2 \,{\rm d} f .$$
- Das linke Diagramm der Grafik zeigt $|H_{\rm E}(f)|^2$ im linearen Maßstab für die charakteristische Kabeldämpfung $a_\star = 80 \ \rm dB$. Beachten Sie, dass $|H_{\rm E}(f = 0)|^2 = 1$ ist.
- Da die Frequenz in dieser Darstellung auf $1/T$ normiert wurde, entspricht die normierte Störleistung genau der (rot hinterlegten) Fläche unter dieser Kurve. Die numerische Auswertung ergibt:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = 1.68 \cdot 10^7\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 \approx 72.25\,{\rm dB} \hspace{0.05cm}.$$
- Es kann gezeigt werden, dass die normierte Störleistung allein mit dem Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ berechnet werden kann, wie in der rechten Grafik dargestellt:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{-1/(2T)}^{+1/(2T)} H_{\rm TF}(f) \,{\rm d} f \hspace{0.3cm}(= k_0)\hspace{0.05cm}.$$
- Die roten Flächen sind in beiden Bildern exakt gleich.
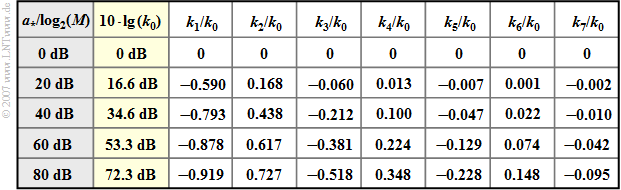
$\text{Fazit:}$ Die normierten Störleistung des optimalen Nyquistentzerrers ist gleich dem Fourierkoeffizienten $k_0$, wenn man den reellen, symmetrischen und periodischen Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ als Fourierreihe darstellt.
- In der zweiten Spalte der Tabelle ist $10 \cdot \lg \ (k_0)$ abhängig von der charakteristischen Kabeldämpfung $a_\star$ eines Koaxialkabels angegeben.
- Aufgrund der gewählten Normierung gilt die Tabelle auch für "redundanzfreie Mehrstufensysteme"; hierbei bezeichnet $M$ die Stufenzahl.
- Die Koeffizienten $k_1$, $k_2$, $k_3$, ... des Transversalfilters weisen für $a_\star \ne 0 \ \rm dB$ alternierende Vorzeichen auf.
- Für $a_\star = 40 \ \rm dB$ sind vier Koeffizienten betragsmäßig größer als $k_0/10$, für $a_\star = 80 \ \rm dB$ sogar sieben.
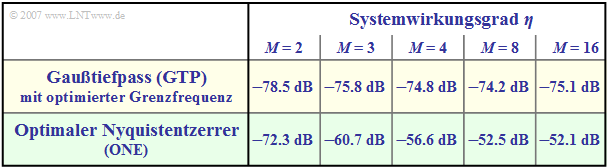
Vergleich anhand des Systemwirkungsgrades
Für einen Systemvergleich eignet sich der "Systemwirkungsgrad", der das erreichbare Detektions–SNR $\rho_d$ in Bezug zum maximalen SNR $\rho_{d, \ {\rm max}}$ setzt, das allerdings nur bei idealem Kanal $H_{\rm K}(f) \equiv 1$ erreichbar ist.
Für den Systemwirkungsgrad gilt bei $M$–stufiger Übertragung und optimaler Nyquistentzerrung:
- $$\eta = \frac{\rho_d}{s_0^2 \cdot T / N_0}=\frac{{\rm log_2}\hspace{0.1cm}M}{(M-1)^2 \cdot k_0}.$$
- Die (normierte) Störleistung $k_0$ kann aus der Tabelle auf der letzten Seite abgelesen werden.
- Beachten Sie die Normierung der charakteristischen Kabeldämpfung $a_\star$ in der ersten Spalte.
- Die Tabelle aus [ST85][1] ermöglicht einen Systemvergleich für die charakteristische Kabeldämpfung $a_\star = 80 \ \rm dB$.
Verglichen werden:
- der "gaußförmige Gesamtfrequenzgang" $\text{(GTP)}$, der auch bei Optimierung zu einem impulsinterferenzbehafteten System führt,
- der "optimale Nyquistentzerrer" $\text{(ONE)}$, mit dem Impulsinterferenzen per se ausgeschlossen werden.
$\text{Fazit:}$ Die Ergebnisse dieses Systemvergleichs können wie folgt zusammengefasst werden:
- Im binären Fall $(M = 2)$ ist das impulsinterferenzfreie System $\text{(ONE)}$ um etwa $6 \ \rm dB$ besser als das impulsinterferenzbehaftete System $\text{(GTP)}$.
- Wendet man die optimale Nyquistentzerrung bei Mehrstufensystemen an, so ist gegenüber $\text{GTP}$ ein weiterer, deutlicher Störabstandsgewinn möglich.
- Für $M =4$ beträgt dieser Gewinn etwa $18.2 \ \rm dB$.
- Das schmalbandige $\text{GTP}$–System kann allerdings deutlich verbessert werden, wenn man einen Empfänger mit Entscheidungsrückkopplung verwendet.
- Dieser wird im nächsten Kapitel behandelt.
⇒ Wir verweisen an dieser Stelle auf das interaktive SWF–Applet "Lineare Nyquistentzerrung".
Aufgaben zum Kapitel
Aufgabe 3.6: Transversalfilter des Optimalen Nyquistentzerrers
Aufgabe 3.6Z: Optimaler Nyquistentzerrer für Exponentialimpuls
Aufgabe 3.7: Nochmals Optimale Nyquistentzerrung
Aufgabe 3.7Z: Regeneratorfeldlänge
Quellenverzeichnis