Aufgaben:Aufgabe 2.5Z: Mehrwege-Szenario: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
[[Datei:P_ID2169__Mob_Z_2_5.png|right|frame|Mobilfunk–Szenario mit drei Pfaden]] | [[Datei:P_ID2169__Mob_Z_2_5.png|right|frame|Mobilfunk–Szenario mit drei Pfaden]] | ||
| − | In [[Aufgaben:2.5_Scatter-Funktion| Aufgabe 2.5]] war die Verzögerungs–Doppler–Funktion vorgegeben. Daraus sollte man die anderen Systemfunktionen berechnen und interpretieren. Die Vorgabe für die Scatterfunktion $s(\tau_0, f_{\rm D})$ lautete: | + | In [[Aufgaben:2.5_Scatter-Funktion| Aufgabe 2.5]] war die Verzögerungs–Doppler–Funktion vorgegeben. Daraus sollte man die anderen Systemfunktionen berechnen und interpretieren. Die Vorgabe für die Scatterfunktion $s(\tau_0, f_{\rm D})$ lautete: |
| − | :$$s(\tau_0, f_{\rm D}) =\frac{1}{\sqrt{2}} \cdot \delta (\tau_0) \cdot \delta (f_{\rm D} - 100\,{\rm Hz}) \ - \ $$ | + | :$$s(\tau_0,\ f_{\rm D}) =\frac{1}{\sqrt{2}} \cdot \delta (\tau_0) \cdot \delta (f_{\rm D} - 100\,{\rm Hz}) \ - \ $$ |
| − | :$$\hspace{1.5cm} \ - \ \hspace{-0.2cm} \frac{1}{2} \cdot \delta (\tau_0 \hspace{-0.05cm}- \hspace{-0.05cm}1\,{\rm | + | :$$\hspace{1.5cm} \ - \ \hspace{-0.2cm} \frac{1}{2} \cdot \delta (\tau_0 \hspace{-0.05cm}- \hspace{-0.05cm}1\,{\rm µ s}) \cdot \delta (f_{\rm D} \hspace{-0.05cm}- \hspace{-0.05cm}50\,{\rm Hz}) \ - \frac{1}{2} \cdot \delta (\tau_0 \hspace{-0.05cm}- \hspace{-0.05cm}1\,{\rm µ s}) \cdot \delta (f_{\rm D}\hspace{-0.05cm} + \hspace{-0.05cm}50\,{\rm Hz}) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | ''Hinweis:'' In unserem Lerntutorial wird $s(\tau_0, \hspace{0. | + | ''Hinweis:'' In unserem Lerntutorial wird $s(\tau_0, \hspace{0.1cm} f_{\rm D})$ auch mit $\eta_{\rm VD}(\tau_0, \hspace{0.1cm}f_{\rm D})$ bezeichnet. |
| − | Wir haben hier die Verzögerungsvariable $\tau$ durch $\tau_0$ ersetzt. Dabei beschreibt die neue Variable $\tau_0$ die Differenz zwischen der Laufzeit eines Pfades und der Laufzeit $\tau_1$ des Hauptpfades. Der Hauptpfad ist somit in obiger Gleichung durch $\tau_0 = 0$ gekennzeichnet. | + | Wir haben hier die Verzögerungsvariable $\tau$ durch $\tau_0$ ersetzt. Dabei beschreibt die neue Variable $\tau_0$ die Differenz zwischen der Laufzeit eines Pfades und der Laufzeit $\tau_1$ des Hauptpfades. Der Hauptpfad ist somit in obiger Gleichung durch $\tau_0 = 0$ gekennzeichnet. |
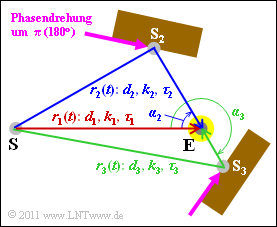
| − | Nun wird versucht, ein Mobilfunkszenario zu finden, bei dem tatsächlich diese Scatterfunktion auftreten würde. Die Grundstruktur ist dabei oben als Draufsicht skizziert, und es gilt: | + | Nun wird versucht, ein Mobilfunkszenario zu finden, bei dem tatsächlich diese Scatterfunktion auftreten würde. Die Grundstruktur ist dabei oben als Draufsicht skizziert, und es gilt: |
* Gesendet wird eine einzige Frequenz $f_{\rm S} = 2 \ \rm GHz$. | * Gesendet wird eine einzige Frequenz $f_{\rm S} = 2 \ \rm GHz$. | ||
| − | * Der mobile Empfänger $\rm (E)$ ist hier durch einen gelben Punkt dargestellt. Nicht bekannt ist, ob das Fahrzeugt steht, sich auf den Sender $\rm (S)$ zu bewegt oder sich von diesem entfernt. | + | * Der mobile Empfänger $\rm (E)$ ist hier durch einen gelben Punkt dargestellt. Nicht bekannt ist, ob das Fahrzeugt steht, sich auf den Sender $\rm (S)$ zu bewegt oder sich von diesem entfernt. |
| − | * Das Signal gelangt über einen Hauptpfad (rot) und zwei Nebenpfaden (blau und grün) zum Empfänger. Reflexionen an den Hindernissen führen jeweils zu Phasendrehungen um $\pi$. | + | * Das Signal gelangt über einen Hauptpfad (rot) und zwei Nebenpfaden (blau und grün) zum Empfänger. Reflexionen an den Hindernissen führen jeweils zu Phasendrehungen um $\pi$. |
* ${\rm S}_2$ und ${\rm S}_3$ sind hier als fiktive Sender zu verstehen, aus deren Lage die Auftreffwinkel $\alpha_2$ und $\alpha_3$ der Nebenpfade ermittelt werden können. | * ${\rm S}_2$ und ${\rm S}_3$ sind hier als fiktive Sender zu verstehen, aus deren Lage die Auftreffwinkel $\alpha_2$ und $\alpha_3$ der Nebenpfade ermittelt werden können. | ||
* Für die Dopplerfrequenz gilt mit der Signalfrequenz $f_{\rm S}$, dem Winkel $\alpha$, der Geschwindigkeit $v$ und der Lichtgeschwindigkeit $c = 3 \cdot 10^8 \ \rm m/s$: | * Für die Dopplerfrequenz gilt mit der Signalfrequenz $f_{\rm S}$, dem Winkel $\alpha$, der Geschwindigkeit $v$ und der Lichtgeschwindigkeit $c = 3 \cdot 10^8 \ \rm m/s$: | ||
:$$f_{\rm D}= {v}/{c} \cdot f_{\rm S} \cdot \cos(\alpha) | :$$f_{\rm D}= {v}/{c} \cdot f_{\rm S} \cdot \cos(\alpha) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * Die Dämpfungsfaktoren $k_1$, $k_2$ und $k_3$ sind umgekehrt proportional zu den Pfadlängen $d_1$, $d_2$ und $d_3$. Dies entspricht dem Pfadverlustexponenten $\gamma = 2$. | + | * Die Dämpfungsfaktoren $k_1$, $k_2$ und $k_3$ sind umgekehrt proportional zu den Pfadlängen $d_1$, $d_2$ und $d_3$. Dies entspricht dem Pfadverlustexponenten $\gamma = 2$. |
*Das bedeutet: Die Signalleistung nimmt quadratisch mit der Distanz $d$ ab und dementsprechend die Signalamplitude linear mit $d$. | *Das bedeutet: Die Signalleistung nimmt quadratisch mit der Distanz $d$ ab und dementsprechend die Signalamplitude linear mit $d$. | ||
| + | |||
| + | |||
| + | |||
| Zeile 39: | Zeile 42: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Betrachten Sie zunächst nur die Diracfunktion bei $\tau = 0$ und $f_{\rm D} = 100 \ \rm Hz$. Welche Aussagen gelten für den Empfänger? | + | {Betrachten Sie zunächst nur die Diracfunktion bei $\tau = 0$ und $f_{\rm D} = 100 \ \rm Hz$. Welche Aussagen gelten für den Empfänger? |
| − | |type=" | + | |type="()"} |
- Der Empfänger steht. | - Der Empfänger steht. | ||
+ Der Empfänger fährt direkt auf den Sender zu. | + Der Empfänger fährt direkt auf den Sender zu. | ||
| Zeile 84: | Zeile 87: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die Dopplerfrequenz ist für $\tau_0$ positiv. Das heißt, dass sich der Empfänger auf den Sender zu bewegt ⇒ <u>Aussage 2</u>. | + | '''(1)''' Die Dopplerfrequenz ist für $\tau_0$ positiv. Das heißt, dass sich der Empfänger auf den Sender zu bewegt ⇒ <u>Aussage 2</u>. |
| − | '''(2)''' Die Gleichung für die Dopplerfrequenz lautet allgemein bzw. für den | + | |
| + | '''(2)''' Die Gleichung für die Dopplerfrequenz lautet allgemein bzw. für den Winke l $\alpha = 0$: | ||
:$$f_{\rm D}= \frac{v}{c} \cdot f_{\rm S} \cdot \cos(\alpha) | :$$f_{\rm D}= \frac{v}{c} \cdot f_{\rm S} \cdot \cos(\alpha) | ||
\hspace{0.05cm},\hspace{0.3cm}\alpha = 0 \hspace{0.05cm}{\rm :} \hspace{0.15cm}f_{\rm D}= \frac{v}{c} \cdot f_{\rm S}\hspace{0.05cm}.$$ | \hspace{0.05cm},\hspace{0.3cm}\alpha = 0 \hspace{0.05cm}{\rm :} \hspace{0.15cm}f_{\rm D}= \frac{v}{c} \cdot f_{\rm S}\hspace{0.05cm}.$$ | ||
| − | Daraus erhält man für die Geschwindigkeit | + | *Daraus erhält man für die Geschwindigkeit: |
:$$v = \frac{f_{\rm D}}{f_{\rm S}} \cdot c = \frac{10^2\,{\rm Hz}}{2 \cdot 10^9\,{\rm Hz}} \cdot 3 \cdot 10^8\,{\rm m/s} = 15\,{\rm m/s} | :$$v = \frac{f_{\rm D}}{f_{\rm S}} \cdot c = \frac{10^2\,{\rm Hz}}{2 \cdot 10^9\,{\rm Hz}} \cdot 3 \cdot 10^8\,{\rm m/s} = 15\,{\rm m/s} | ||
\hspace{0.1cm} \underline {= 54 \,{\rm km/h}} | \hspace{0.1cm} \underline {= 54 \,{\rm km/h}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | |||
'''(3)''' Richtig sind die <u>Lösungsvorschläge 1 und 4</u>: | '''(3)''' Richtig sind die <u>Lösungsvorschläge 1 und 4</u>: | ||
| − | *Die Dopplerfrequenz $f_{\rm D} = 50 \ \rm Hz$ rührt vom blauen Pfad her, da sich der Empfänger irgendwie auf den virtuellen Sender ${\rm S}_2$ (beim Reflexionspunkt) zubewegt, wenn auch nicht in direkter Richtung. | + | *Die Dopplerfrequenz $f_{\rm D} = 50 \ \rm Hz$ rührt vom blauen Pfad her, da sich der Empfänger irgendwie auf den virtuellen Sender ${\rm S}_2$ (beim Reflexionspunkt) zubewegt, wenn auch nicht in direkter Richtung. |
| − | *Der Winkel $\alpha_2$ zwischen der Bewegungsrichtung und der Verbindungslinie ${\rm S_2 | + | *Der Winkel $\alpha_2$ zwischen der Bewegungsrichtung und der Verbindungslinie ${\rm S_2 - E}$ beträgt $60^\circ$: |
:$$\cos(\alpha_2) = \frac{f_{\rm D}}{f_{\rm S}} \cdot \frac{c}{v} = \frac{50 \,{\rm Hz}\cdot 3 \cdot 10^8\,{\rm m/s}}{2 \cdot 10^9\,{\rm Hz}\cdot 15\,{\rm m/s}} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \alpha_2 | :$$\cos(\alpha_2) = \frac{f_{\rm D}}{f_{\rm S}} \cdot \frac{c}{v} = \frac{50 \,{\rm Hz}\cdot 3 \cdot 10^8\,{\rm m/s}}{2 \cdot 10^9\,{\rm Hz}\cdot 15\,{\rm m/s}} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \alpha_2 | ||
\hspace{0.1cm} \underline {= 60^{\circ} } | \hspace{0.1cm} \underline {= 60^{\circ} } | ||
| Zeile 105: | Zeile 110: | ||
| − | '''(4)''' Richtig sind die <u>Aussagen 1 und 3</u> | + | |
| + | '''(4)''' Richtig sind die <u>Aussagen 1 und 3</u>: | ||
| + | *Aus $f_{\rm D} = \, –50 \ \rm Hz$ folgt $\alpha_3 = \alpha_2 ± \pi$, also $\alpha_3 \ \underline {= 240^\circ}$. | ||
| + | |||
| + | |||
'''(5)''' <u>Alle Aussagen stimmen</u>: | '''(5)''' <u>Alle Aussagen stimmen</u>: | ||
| − | *Die beiden Diracfunktionen bei $± 50 \ \rm Hz$ haben die gleiche Laufzeit. Für beide Laufzeiten gilt $\tau_3 = \tau_2 = \tau_1 + \tau_0$. | + | *Die beiden Diracfunktionen bei $± 50 \ \rm Hz$ haben die gleiche Laufzeit. Für beide Laufzeiten gilt $\tau_3 = \tau_2 = \tau_1 + \tau_0$. |
| − | *Aus der gleichen Laufzeit folgt aber auch $d_3 = d_2$ und bei gleicher Länge auch die gleichen Dämpfungsfaktoren. | + | *Aus der gleichen Laufzeit folgt aber auch $d_3 = d_2$ und bei gleicher Länge auch die gleichen Dämpfungsfaktoren. |
| + | |||
| + | |||
| − | '''(6)''' Die Laufzeitdifferenz ist $\tau_0 = 1 \ \rm | + | '''(6)''' Die Laufzeitdifferenz ist $\tau_0 = 1 \ \rm µ s$, wie aus der Gleichung für $s(\tau_0,\ f_{\rm D})$ hervorgeht. |
| + | * Damit ergibt sich die Längendifferenz: | ||
:$$\Delta d = \tau_0 \cdot c = 10^{–6} {\rm s} \cdot 3 \cdot 10^8 \ \rm m/s \ \underline {= 300 \ \rm m}.$$ | :$$\Delta d = \tau_0 \cdot c = 10^{–6} {\rm s} \cdot 3 \cdot 10^8 \ \rm m/s \ \underline {= 300 \ \rm m}.$$ | ||
| − | |||
| − | Das Minuszeichen berücksichtigt hierbei die $180^\circ$–Phasendrehung auf den Nebenpfaden. Aus den Gewichten der Diracfunktionen kann man $k_1 = \sqrt{0.5}$ und $k_2 = -0.5$ ablesen. Daraus folgt: | + | '''(7)''' Der Pfadverlustexponent wurde für diese Aufgabe zu $\gamma = 2$ vorausgesetzt. |
| + | *Dann gilt $k_1 = K/d_1$ und $k_2 = K/d_2$. | ||
| + | |||
| + | *Das Minuszeichen berücksichtigt hierbei die $180^\circ$–Phasendrehung auf den Nebenpfaden. | ||
| + | *Aus den Gewichten der Diracfunktionen kann man $k_1 = \sqrt{0.5}$ und $k_2 = -0.5$ ablesen. Daraus folgt: | ||
:$$\frac{d_2}{d_1} = \frac{k_1}{-k_2} = \frac{1/\sqrt{2}}{0.5} = \sqrt{2} | :$$\frac{d_2}{d_1} = \frac{k_1}{-k_2} = \frac{1/\sqrt{2}}{0.5} = \sqrt{2} | ||
\hspace{0.15cm} \underline {= 1.414} | \hspace{0.15cm} \underline {= 1.414} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Die Konstante $K$ ist lediglich eine Hilfsgröße, die nicht weiter betrachtet werden muss. | + | *Die Konstante $K$ ist lediglich eine Hilfsgröße, die nicht weiter betrachtet werden muss. |
| + | |||
| − | '''(8)''' Aus $d_2/d_1 = 2^{ | + | '''(8)''' Aus $d_2/d_1 = 2^{-0.5}$ und $\Delta d = d_2 \, - d_1 = 300 \ \rm m$ folgt schließlich: |
:$$\sqrt{2} \cdot d_1 - d_1 = 300\,{\rm m} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | :$$\sqrt{2} \cdot d_1 - d_1 = 300\,{\rm m} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
d_1 = \frac{300\,{\rm m}}{\sqrt{2} - 1} \hspace{0.15cm} \underline {= 724\,{\rm m}} | d_1 = \frac{300\,{\rm m}}{\sqrt{2} - 1} \hspace{0.15cm} \underline {= 724\,{\rm m}} | ||
Aktuelle Version vom 25. Mai 2020, 14:56 Uhr
In Aufgabe 2.5 war die Verzögerungs–Doppler–Funktion vorgegeben. Daraus sollte man die anderen Systemfunktionen berechnen und interpretieren. Die Vorgabe für die Scatterfunktion $s(\tau_0, f_{\rm D})$ lautete:
- $$s(\tau_0,\ f_{\rm D}) =\frac{1}{\sqrt{2}} \cdot \delta (\tau_0) \cdot \delta (f_{\rm D} - 100\,{\rm Hz}) \ - \ $$
- $$\hspace{1.5cm} \ - \ \hspace{-0.2cm} \frac{1}{2} \cdot \delta (\tau_0 \hspace{-0.05cm}- \hspace{-0.05cm}1\,{\rm µ s}) \cdot \delta (f_{\rm D} \hspace{-0.05cm}- \hspace{-0.05cm}50\,{\rm Hz}) \ - \frac{1}{2} \cdot \delta (\tau_0 \hspace{-0.05cm}- \hspace{-0.05cm}1\,{\rm µ s}) \cdot \delta (f_{\rm D}\hspace{-0.05cm} + \hspace{-0.05cm}50\,{\rm Hz}) \hspace{0.05cm}.$$
Hinweis: In unserem Lerntutorial wird $s(\tau_0, \hspace{0.1cm} f_{\rm D})$ auch mit $\eta_{\rm VD}(\tau_0, \hspace{0.1cm}f_{\rm D})$ bezeichnet.
Wir haben hier die Verzögerungsvariable $\tau$ durch $\tau_0$ ersetzt. Dabei beschreibt die neue Variable $\tau_0$ die Differenz zwischen der Laufzeit eines Pfades und der Laufzeit $\tau_1$ des Hauptpfades. Der Hauptpfad ist somit in obiger Gleichung durch $\tau_0 = 0$ gekennzeichnet.
Nun wird versucht, ein Mobilfunkszenario zu finden, bei dem tatsächlich diese Scatterfunktion auftreten würde. Die Grundstruktur ist dabei oben als Draufsicht skizziert, und es gilt:
- Gesendet wird eine einzige Frequenz $f_{\rm S} = 2 \ \rm GHz$.
- Der mobile Empfänger $\rm (E)$ ist hier durch einen gelben Punkt dargestellt. Nicht bekannt ist, ob das Fahrzeugt steht, sich auf den Sender $\rm (S)$ zu bewegt oder sich von diesem entfernt.
- Das Signal gelangt über einen Hauptpfad (rot) und zwei Nebenpfaden (blau und grün) zum Empfänger. Reflexionen an den Hindernissen führen jeweils zu Phasendrehungen um $\pi$.
- ${\rm S}_2$ und ${\rm S}_3$ sind hier als fiktive Sender zu verstehen, aus deren Lage die Auftreffwinkel $\alpha_2$ und $\alpha_3$ der Nebenpfade ermittelt werden können.
- Für die Dopplerfrequenz gilt mit der Signalfrequenz $f_{\rm S}$, dem Winkel $\alpha$, der Geschwindigkeit $v$ und der Lichtgeschwindigkeit $c = 3 \cdot 10^8 \ \rm m/s$:
- $$f_{\rm D}= {v}/{c} \cdot f_{\rm S} \cdot \cos(\alpha) \hspace{0.05cm}.$$
- Die Dämpfungsfaktoren $k_1$, $k_2$ und $k_3$ sind umgekehrt proportional zu den Pfadlängen $d_1$, $d_2$ und $d_3$. Dies entspricht dem Pfadverlustexponenten $\gamma = 2$.
- Das bedeutet: Die Signalleistung nimmt quadratisch mit der Distanz $d$ ab und dementsprechend die Signalamplitude linear mit $d$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Das GWSSUS–Kanalmodell.
- Bezug genommen wird insbesondere auf das Pfadverlustmodell und den Dopplereffekt.
Fragebogen
Musterlösung
(2) Die Gleichung für die Dopplerfrequenz lautet allgemein bzw. für den Winke l $\alpha = 0$:
- $$f_{\rm D}= \frac{v}{c} \cdot f_{\rm S} \cdot \cos(\alpha) \hspace{0.05cm},\hspace{0.3cm}\alpha = 0 \hspace{0.05cm}{\rm :} \hspace{0.15cm}f_{\rm D}= \frac{v}{c} \cdot f_{\rm S}\hspace{0.05cm}.$$
- Daraus erhält man für die Geschwindigkeit:
- $$v = \frac{f_{\rm D}}{f_{\rm S}} \cdot c = \frac{10^2\,{\rm Hz}}{2 \cdot 10^9\,{\rm Hz}} \cdot 3 \cdot 10^8\,{\rm m/s} = 15\,{\rm m/s} \hspace{0.1cm} \underline {= 54 \,{\rm km/h}} \hspace{0.05cm}.$$
(3) Richtig sind die Lösungsvorschläge 1 und 4:
- Die Dopplerfrequenz $f_{\rm D} = 50 \ \rm Hz$ rührt vom blauen Pfad her, da sich der Empfänger irgendwie auf den virtuellen Sender ${\rm S}_2$ (beim Reflexionspunkt) zubewegt, wenn auch nicht in direkter Richtung.
- Der Winkel $\alpha_2$ zwischen der Bewegungsrichtung und der Verbindungslinie ${\rm S_2 - E}$ beträgt $60^\circ$:
- $$\cos(\alpha_2) = \frac{f_{\rm D}}{f_{\rm S}} \cdot \frac{c}{v} = \frac{50 \,{\rm Hz}\cdot 3 \cdot 10^8\,{\rm m/s}}{2 \cdot 10^9\,{\rm Hz}\cdot 15\,{\rm m/s}} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \alpha_2 \hspace{0.1cm} \underline {= 60^{\circ} } \hspace{0.05cm}.$$
(4) Richtig sind die Aussagen 1 und 3:
- Aus $f_{\rm D} = \, –50 \ \rm Hz$ folgt $\alpha_3 = \alpha_2 ± \pi$, also $\alpha_3 \ \underline {= 240^\circ}$.
(5) Alle Aussagen stimmen:
- Die beiden Diracfunktionen bei $± 50 \ \rm Hz$ haben die gleiche Laufzeit. Für beide Laufzeiten gilt $\tau_3 = \tau_2 = \tau_1 + \tau_0$.
- Aus der gleichen Laufzeit folgt aber auch $d_3 = d_2$ und bei gleicher Länge auch die gleichen Dämpfungsfaktoren.
(6) Die Laufzeitdifferenz ist $\tau_0 = 1 \ \rm µ s$, wie aus der Gleichung für $s(\tau_0,\ f_{\rm D})$ hervorgeht.
- Damit ergibt sich die Längendifferenz:
- $$\Delta d = \tau_0 \cdot c = 10^{–6} {\rm s} \cdot 3 \cdot 10^8 \ \rm m/s \ \underline {= 300 \ \rm m}.$$
(7) Der Pfadverlustexponent wurde für diese Aufgabe zu $\gamma = 2$ vorausgesetzt.
- Dann gilt $k_1 = K/d_1$ und $k_2 = K/d_2$.
- Das Minuszeichen berücksichtigt hierbei die $180^\circ$–Phasendrehung auf den Nebenpfaden.
- Aus den Gewichten der Diracfunktionen kann man $k_1 = \sqrt{0.5}$ und $k_2 = -0.5$ ablesen. Daraus folgt:
- $$\frac{d_2}{d_1} = \frac{k_1}{-k_2} = \frac{1/\sqrt{2}}{0.5} = \sqrt{2} \hspace{0.15cm} \underline {= 1.414} \hspace{0.05cm}.$$
- Die Konstante $K$ ist lediglich eine Hilfsgröße, die nicht weiter betrachtet werden muss.
(8) Aus $d_2/d_1 = 2^{-0.5}$ und $\Delta d = d_2 \, - d_1 = 300 \ \rm m$ folgt schließlich:
- $$\sqrt{2} \cdot d_1 - d_1 = 300\,{\rm m} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} d_1 = \frac{300\,{\rm m}}{\sqrt{2} - 1} \hspace{0.15cm} \underline {= 724\,{\rm m}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} d_2 = \sqrt{2} \cdot d_1 \hspace{0.15cm} \underline {= 1024\,{\rm m}} \hspace{0.05cm}. $$