Aufgaben:Aufgabe 2.7Z: Huffman-Codierung für Zweiertupel einer Ternärquelle: Unterschied zwischen den Versionen
Aus LNTwww
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2458__Inf_Z_2_7.png|right|frame|Huffman–Baum für Ternärquelle]] | + | [[Datei:P_ID2458__Inf_Z_2_7.png|right|frame|Huffman–Baum für <br>eine Ternärquelle]] |
| − | Wir betrachten den gleichen Sachverhalt wie in der [[Aufgaben:2.7_Huffman-Anwendung_für_binäre_Zweiertupel|Aufgabe A2.7]]: Der Huffman–Algorithmus führt zu einem besseren Ergebnis, das heißt zu einer kleineren mittleren Codewortlänge $L_{\rm M}$, wenn man ihn nicht auf einzelne Symbole anwendet, sondern vorher $k$–Tupel bildet. Dadurch erhöht man den Symbolumfang von $M$ auf $M' = M^k$. | + | Wir betrachten den gleichen Sachverhalt wie in der [[Aufgaben:2.7_Huffman-Anwendung_für_binäre_Zweiertupel|Aufgabe A2.7]]: |
| + | *Der Huffman–Algorithmus führt zu einem besseren Ergebnis, das heißt zu einer kleineren mittleren Codewortlänge $L_{\rm M}$, wenn man ihn nicht auf einzelne Symbole anwendet, sondern vorher $k$–Tupel bildet. | ||
| + | *Dadurch erhöht man den Symbolumfang von $M$ auf $M\hspace{0.03cm}' = M^k$. | ||
| + | |||
Für die hier betrachtete Nachrichtenquelle gilt: | Für die hier betrachtete Nachrichtenquelle gilt: | ||
* Symbolumfang: $M = 3$, | * Symbolumfang: $M = 3$, | ||
| − | * Symbolvorrat: $\{$ $\rm X$, $\rm Y$, $\rm Z$ $\}$, | + | * Symbolvorrat: $\{$ $\rm X$, $\rm Y$, $\rm Z$ $\}$, |
| − | * Wahrscheinlichkeiten: $p_{\rm X} = 0.7$, $p_{\rm Y} = 0.2$, $p_{\rm Z} = 0.1$, | + | * Wahrscheinlichkeiten: $p_{\rm X} = 0.7$, $p_{\rm Y} = 0.2$, $p_{\rm Z} = 0.1$, |
* Entropie: $H = 1.157 \ \rm bit/Ternärsymbol$. | * Entropie: $H = 1.157 \ \rm bit/Ternärsymbol$. | ||
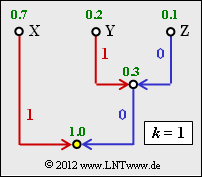
| − | Die Grafik zeigt den Huffman–Baum, wenn man den Huffman–Algorithmus auf Einzelsymbole anwendet, also den Fall $k= 1$. In der Teilaufgabe '''(2)''' sollen Sie den entsprechenden Huffman–Code angeben, wenn vorher Zweiertupel gebildet werden $(k=2)$. | + | Die Grafik zeigt den Huffman–Baum, wenn man den Huffman–Algorithmus auf Einzelsymbole anwendet, also den Fall $k= 1$. <br>In der Teilaufgabe '''(2)''' sollen Sie den entsprechenden Huffman–Code angeben, wenn vorher Zweiertupel gebildet werden $(k=2)$. |
| + | |||
| + | |||
| + | |||
| Zeile 20: | Zeile 26: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Entropiecodierung_nach_Huffman|Entropiecodierung nach Huffman]]. | + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Entropiecodierung_nach_Huffman|Entropiecodierung nach Huffman]]. |
| − | *Insbesondere wird auf die Seite [[Informationstheorie/Entropiecodierung_nach_Huffman#Anwendung_der_Huffman.E2.80.93Codierung_auf_.7F.27.22.60UNIQ- | + | *Insbesondere wird auf die Seite [[Informationstheorie/Entropiecodierung_nach_Huffman#Anwendung_der_Huffman.E2.80.93Codierung_auf_.7F.27.22.60UNIQ-MathJax169-QINU.60.22.27.7F.E2.80.93Tupel|Anwendung der Huffman-Codierung auf $k$-Tupel]] Bezug genommen. |
| − | *Eine vergleichbare Aufgabenstellung mit binären Eingangssymbolen wird in der [[Aufgaben:2.7_Huffman-Anwendung_für_binäre_Zweiertupel|Aufgabe 2.7]] behandelt. | + | *Eine vergleichbare Aufgabenstellung mit binären Eingangssymbolen wird in der [[Aufgaben:2.7_Huffman-Anwendung_für_binäre_Zweiertupel|Aufgabe 2.7]] behandelt. |
| − | *Bezeichnen Sie die möglichen Zweiertupel mit $\rm XX = A$, $\rm XY = B$, $\rm XZ = C$, $\rm YX = D$, $\rm YY = E$, $\rm YZ = F$, $\rm ZX = G$, $\rm ZY = H$, $\rm ZZ = I$. | + | *Bezeichnen Sie die möglichen Zweiertupel mit $\rm XX = A$, $\rm XY = B$, $\rm XZ = C$, $\rm YX = D$, $\rm YY = E$, $\rm YZ = F$, $\rm ZX = G$, $\rm ZY = H$, $\rm ZZ = I$. |
| Zeile 30: | Zeile 36: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist die mittlere Codewortlänge, wenn der Huffman–Algorithmus direkt auf die ternären Quellensymbole $\rm X$, $\rm Y$ und $\rm Z$ angewendet wird? | + | {Wie groß ist die mittlere Codewortlänge, wenn der Huffman–Algorithmus direkt auf die ternären Quellensymbole $\rm X$, $\rm Y$ und $\rm Z$ angewendet wird? |
|type="{}"} | |type="{}"} | ||
$\underline{k=1}\text{:} \hspace{0.25cm}L_{\rm M} \ = \ $ { 1.3 3% } $\ \rm bit/Quellensymbol$ | $\underline{k=1}\text{:} \hspace{0.25cm}L_{\rm M} \ = \ $ { 1.3 3% } $\ \rm bit/Quellensymbol$ | ||
| − | {Wie groß sind | + | {Wie groß sind hier die Tupel–Wahrscheinlichkeiten? Insbesondere: |
|type="{}"} | |type="{}"} | ||
$p_{\rm A} = \rm Pr(XX)\ = \ $ { 0.49 3% } | $p_{\rm A} = \rm Pr(XX)\ = \ $ { 0.49 3% } | ||
| Zeile 47: | Zeile 53: | ||
| − | {Welche der folgenden Aussagen sind zutreffend, wenn man mehr als zwei Ternärzeichen zusammenfasst ( | + | {Welche der folgenden Aussagen sind zutreffend, wenn man mehr als zwei Ternärzeichen zusammenfasst $(k>2)$? |
|type="[]"} | |type="[]"} | ||
+ $L_{\rm M}$ fällt monoton mit steigendem $k$ ab. | + $L_{\rm M}$ fällt monoton mit steigendem $k$ ab. | ||
| Zeile 61: | Zeile 67: | ||
'''(1)''' Die mittlere Codewortlänge ergibt sich mit $p_{\rm X} = 0.7$, $L_{\rm X} = 1$, $p_{\rm Y} = 0.2$, $L_{\rm Y} = 2$, $p_{\rm Z} = 0.1$, $L_{\rm Z} = 2$ zu | '''(1)''' Die mittlere Codewortlänge ergibt sich mit $p_{\rm X} = 0.7$, $L_{\rm X} = 1$, $p_{\rm Y} = 0.2$, $L_{\rm Y} = 2$, $p_{\rm Z} = 0.1$, $L_{\rm Z} = 2$ zu | ||
:$$L_{\rm M} = p_{\rm X} \cdot 1 + (p_{\rm Y} + p_{\rm Z}) \cdot 2 \hspace{0.15cm}\underline{= 1.3\,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$ | :$$L_{\rm M} = p_{\rm X} \cdot 1 + (p_{\rm Y} + p_{\rm Z}) \cdot 2 \hspace{0.15cm}\underline{= 1.3\,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$ | ||
| − | Dieser Wert liegt noch deutlich über der Quellenentropie | + | *Dieser Wert liegt noch deutlich über der Quellenentropie $H = 1.157$ bit/Quellensymbol. |
| − | |||
| − | + | '''(2)''' Es gibt $M\hspace{0.03cm}' = M^k = 3^2 = 9$ Zweiertupel mit folgenden Wahrscheinlichkeiten: | |
| − | |||
| − | : | ||
| + | [[Datei:P_ID2459__Inf_Z_2_7c.png|right|frame|Huffman–Baum für Ternärquelle und Zweiertupel]] | ||
| + | :$$p_{\rm A} = \rm Pr(XX) = 0.7 \cdot 0.7\hspace{0.15cm}\underline{= 0.49},$$ | ||
| + | :$$p_{\rm B} = \rm Pr(XY) = 0.7 \cdot 0.2\hspace{0.15cm}\underline{= 0.14},$$ | ||
| + | :$$p_{\rm C} = \rm Pr(XZ) = 0.7 \cdot 0.1\hspace{0.15cm}\underline{= 0.07},$$ | ||
| + | :$$p_{\rm D} = \rm Pr(YX) = 0.2 \cdot 0.7 = 0.14,$$ | ||
| + | :$$p_{\rm E} = \rm Pr(YY) = 0.2 \cdot 0.2 = 0.04,$$ | ||
| + | :$$p_{\rm F} = \rm Pr(YZ) = 0.2 \cdot 0.1 = 0.02,$$ | ||
| + | :$$p_{\rm G} = \rm Pr(ZX) = 0.1 \cdot 0.7 = 0.07,$$ | ||
| + | :$$p_{\rm H} = \rm Pr(ZY) = 0.1 \cdot 0.2 = 0.02,$$ | ||
| + | :$$p_{\rm I} = \rm Pr(ZZ) = 0.1 \cdot 0.1 = 0.01.$$ | ||
| + | <br clear=all> | ||
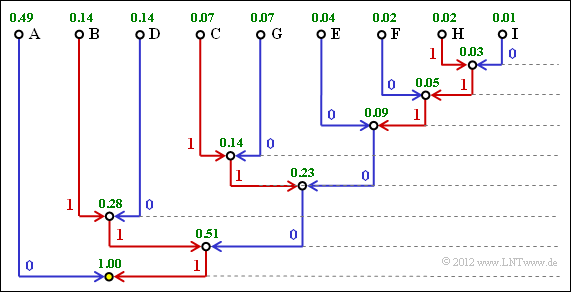
| − | '''(3)''' Die Grafik zeigt den Huffman–Baum für die Anwendung mit | + | '''(3)''' Die Grafik zeigt den Huffman–Baum für die Anwendung mit $k = 2$. Damit erhält man |
| − | |||
| − | |||
| − | |||
| − | Damit erhält man | ||
* für die einzelnen Zweiertupels folgende Binärcodierungen: <br> | * für die einzelnen Zweiertupels folgende Binärcodierungen: <br> | ||
| − | : | + | : $\rm XX = A$ → '''0''', $\rm XY = B$ → '''111''', $\rm XZ = C$ → <b>1011</b>, |
| − | + | : $\rm YX = D$ → <b>110</b>, $\rm YY = E$ → <b>1000</b>, $\rm YZ = F$ → <b>10010</b>, | |
| + | : $\rm ZX = G$ → <b>1010</b>, $\rm ZY = H$ → <b>100111</b>, $\rm ZZ =I$ → <b>100110</b>; | ||
* für die mittlere Codewortlänge: | * für die mittlere Codewortlänge: | ||
| − | :$$L_{\rm M}' =0.49 \cdot 1 + (0.14 + 0.14) \cdot 3 + (0.07 + 0.04 + 0.07) \cdot 4 + 0.02 \cdot 5 + (0.02 + 0.01) \cdot 6 = 2.33\,\,{\rm bit/Zweiertupel}$$ | + | :$$L_{\rm M}\hspace{0.01cm}' =0.49 \cdot 1 + (0.14 + 0.14) \cdot 3 + (0.07 + 0.04 + 0.07) \cdot 4 + 0.02 \cdot 5 + (0.02 + 0.01) \cdot 6 = 2.33\,\,{\rm bit/Zweiertupel}$$ |
| − | :$$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}'}/{2}\hspace{0.15cm}\underline{ = 1.165\,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$ | + | :$$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{2}\hspace{0.15cm}\underline{ = 1.165\,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$ |
| + | |||
| − | '''(4)''' Richtig ist <u>Aussage 1</u>, auch wenn | + | '''(4)''' Richtig ist die <u>Aussage 1</u>, auch wenn $L_{\rm M}$ mit wachsendem $k$ nur sehr langsam abfällt. |
| − | * Die letzte Aussage ist falsch, da | + | * Die letzte Aussage ist falsch, da $L_{\rm M}$ auch für $k → ∞$ nicht kleiner sein kann als $H = 1.157$ bit/Quellensymbol. |
| − | * Aber auch die zweite Aussage ist nicht unbedingt richtig: Da mit | + | * Aber auch die zweite Aussage ist nicht unbedingt richtig: Da mit $k = 2$ weiterhin $L_{\rm M} > H$ gilt, kann $k = 3$ zu einer weiteren Verbesserung führen. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 11. August 2021, 10:49 Uhr
Wir betrachten den gleichen Sachverhalt wie in der Aufgabe A2.7:
- Der Huffman–Algorithmus führt zu einem besseren Ergebnis, das heißt zu einer kleineren mittleren Codewortlänge $L_{\rm M}$, wenn man ihn nicht auf einzelne Symbole anwendet, sondern vorher $k$–Tupel bildet.
- Dadurch erhöht man den Symbolumfang von $M$ auf $M\hspace{0.03cm}' = M^k$.
Für die hier betrachtete Nachrichtenquelle gilt:
- Symbolumfang: $M = 3$,
- Symbolvorrat: $\{$ $\rm X$, $\rm Y$, $\rm Z$ $\}$,
- Wahrscheinlichkeiten: $p_{\rm X} = 0.7$, $p_{\rm Y} = 0.2$, $p_{\rm Z} = 0.1$,
- Entropie: $H = 1.157 \ \rm bit/Ternärsymbol$.
Die Grafik zeigt den Huffman–Baum, wenn man den Huffman–Algorithmus auf Einzelsymbole anwendet, also den Fall $k= 1$.
In der Teilaufgabe (2) sollen Sie den entsprechenden Huffman–Code angeben, wenn vorher Zweiertupel gebildet werden $(k=2)$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Entropiecodierung nach Huffman.
- Insbesondere wird auf die Seite Anwendung der Huffman-Codierung auf $k$-Tupel Bezug genommen.
- Eine vergleichbare Aufgabenstellung mit binären Eingangssymbolen wird in der Aufgabe 2.7 behandelt.
- Bezeichnen Sie die möglichen Zweiertupel mit $\rm XX = A$, $\rm XY = B$, $\rm XZ = C$, $\rm YX = D$, $\rm YY = E$, $\rm YZ = F$, $\rm ZX = G$, $\rm ZY = H$, $\rm ZZ = I$.
Fragebogen
Musterlösung
(1) Die mittlere Codewortlänge ergibt sich mit $p_{\rm X} = 0.7$, $L_{\rm X} = 1$, $p_{\rm Y} = 0.2$, $L_{\rm Y} = 2$, $p_{\rm Z} = 0.1$, $L_{\rm Z} = 2$ zu
- $$L_{\rm M} = p_{\rm X} \cdot 1 + (p_{\rm Y} + p_{\rm Z}) \cdot 2 \hspace{0.15cm}\underline{= 1.3\,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$
- Dieser Wert liegt noch deutlich über der Quellenentropie $H = 1.157$ bit/Quellensymbol.
(2) Es gibt $M\hspace{0.03cm}' = M^k = 3^2 = 9$ Zweiertupel mit folgenden Wahrscheinlichkeiten:
- $$p_{\rm A} = \rm Pr(XX) = 0.7 \cdot 0.7\hspace{0.15cm}\underline{= 0.49},$$
- $$p_{\rm B} = \rm Pr(XY) = 0.7 \cdot 0.2\hspace{0.15cm}\underline{= 0.14},$$
- $$p_{\rm C} = \rm Pr(XZ) = 0.7 \cdot 0.1\hspace{0.15cm}\underline{= 0.07},$$
- $$p_{\rm D} = \rm Pr(YX) = 0.2 \cdot 0.7 = 0.14,$$
- $$p_{\rm E} = \rm Pr(YY) = 0.2 \cdot 0.2 = 0.04,$$
- $$p_{\rm F} = \rm Pr(YZ) = 0.2 \cdot 0.1 = 0.02,$$
- $$p_{\rm G} = \rm Pr(ZX) = 0.1 \cdot 0.7 = 0.07,$$
- $$p_{\rm H} = \rm Pr(ZY) = 0.1 \cdot 0.2 = 0.02,$$
- $$p_{\rm I} = \rm Pr(ZZ) = 0.1 \cdot 0.1 = 0.01.$$
(3) Die Grafik zeigt den Huffman–Baum für die Anwendung mit $k = 2$. Damit erhält man
- für die einzelnen Zweiertupels folgende Binärcodierungen:
- $\rm XX = A$ → 0, $\rm XY = B$ → 111, $\rm XZ = C$ → 1011,
- $\rm YX = D$ → 110, $\rm YY = E$ → 1000, $\rm YZ = F$ → 10010,
- $\rm ZX = G$ → 1010, $\rm ZY = H$ → 100111, $\rm ZZ =I$ → 100110;
- für die mittlere Codewortlänge:
- $$L_{\rm M}\hspace{0.01cm}' =0.49 \cdot 1 + (0.14 + 0.14) \cdot 3 + (0.07 + 0.04 + 0.07) \cdot 4 + 0.02 \cdot 5 + (0.02 + 0.01) \cdot 6 = 2.33\,\,{\rm bit/Zweiertupel}$$
- $$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{2}\hspace{0.15cm}\underline{ = 1.165\,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$
(4) Richtig ist die Aussage 1, auch wenn $L_{\rm M}$ mit wachsendem $k$ nur sehr langsam abfällt.
- Die letzte Aussage ist falsch, da $L_{\rm M}$ auch für $k → ∞$ nicht kleiner sein kann als $H = 1.157$ bit/Quellensymbol.
- Aber auch die zweite Aussage ist nicht unbedingt richtig: Da mit $k = 2$ weiterhin $L_{\rm M} > H$ gilt, kann $k = 3$ zu einer weiteren Verbesserung führen.