| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
==Allgemeine Beschreibung== | ==Allgemeine Beschreibung== | ||
<br> | <br> | ||
| − | Jede periodische Funktion $x(t)$ kann in allen Bereichen, in denen sie stetig ist oder nur endlich viele Sprungstellen aufweist, in eine trigonometrische Reihe entwickelt werden, die man als Fourierreihe bezeichnet. | + | Jede periodische Funktion $x(t)$ kann in allen Bereichen, in denen sie stetig ist oder nur endlich viele Sprungstellen aufweist, in eine trigonometrische Reihe entwickelt werden, die man als Fourierreihe bezeichnet. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Die | + | Die $\text{Fourierreihe}$ eines periodischen Signals $x(t)$ lautet wie folgt: |
:$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t).$$ | :$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t).$$ | ||
Hierbei bezeichnen: | Hierbei bezeichnen: | ||
| − | *$A_0$ den | + | *$A_0$ den $\text{Gleichanteil}$ von $x(t)$, |
| − | *$A_n$ die | + | *$A_n$ die $\text{Cosinuskoeffizienten}$ mit $n \ge 1$, |
| − | *$B_n$ die | + | *$B_n$ die $\text{Sinuskoeffizienten}$ mit $n \ge 1$, |
| − | *$\omega_0 = 2\pi/T_0$ die | + | *$\omega_0 = 2\pi/T_0$ die $\text{Grundkreisfrequenz}$ des periodischen Signals $(T_0$ ist die Periodendauer$)$.}} |
| − | Soll die Fourierreihe mit dem tatsächlichen periodischen Signal $x(t)$ exakt übereinstimmen, so müssen im Allgemeinen unendlich viele Cosinus– und Sinuskoeffizienten zur Berechnung herangezogen werden. | + | Soll die Fourierreihe mit dem tatsächlichen periodischen Signal $x(t)$ exakt übereinstimmen, so müssen im Allgemeinen unendlich viele Cosinus– und Sinuskoeffizienten zur Berechnung herangezogen werden. |
| − | *Bricht man die Fourierreihe ab und verwendet jeweils nur $N$ | + | *Bricht man die Fourierreihe ab und verwendet jeweils nur $N$ Koeffizienten $A_n$ und $B_n$, so ergibt sich bis auf einige Sonderfälle ein etwas anderer Funktionsverlauf: |
:$$x_ N(t) =A_0+\sum^N_{n=1}A_ n \cdot \cos(n \omega_0 t)+\sum^N_{n=1} B_{n} \cdot \sin(n \omega_0 t).$$ | :$$x_ N(t) =A_0+\sum^N_{n=1}A_ n \cdot \cos(n \omega_0 t)+\sum^N_{n=1} B_{n} \cdot \sin(n \omega_0 t).$$ | ||
| − | *Zwischen dem periodischen Signal $x(t)$ und der Fourierreihenapproximation $x_N(t)$ gilt der Zusammenhang: | + | *Zwischen dem periodischen Signal $x(t)$ und der Fourierreihenapproximation $x_N(t)$ gilt der Zusammenhang: |
:$$x(t)=\lim_{N\to \infty} x_{N}(t).$$ | :$$x(t)=\lim_{N\to \infty} x_{N}(t).$$ | ||
| − | *Ist $N \cdot f_0$ die höchste im Signal $x(t)$ vorkommende Frequenz, so gilt natürlich $x_N(t) = x(t)$. | + | *Ist $N \cdot f_0$ die höchste im Signal $x(t)$ vorkommende Frequenz, so gilt natürlich $x_N(t) = x(t)$. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 1:}$ | $\text{Beispiel 1:}$ | ||
| − | Wir betrachten zwei periodische Rechtecksignale, jeweils mit der Periodendauer $T_0$ und der Grundkreisfrequenz $\omega_0 = 2\pi/T_0$. | + | Wir betrachten zwei periodische Rechtecksignale, jeweils mit der Periodendauer $T_0$ und der Grundkreisfrequenz $\omega_0 = 2\pi/T_0$. |
[[Datei:P_ID525__Sig_T_2_4_S1_neu.png|right|frame|Gerades und ungerades Rechtecksignal]] | [[Datei:P_ID525__Sig_T_2_4_S1_neu.png|right|frame|Gerades und ungerades Rechtecksignal]] | ||
*Für das oben skizzierte gerade Zeitsignal gilt: $x_{\rm g}(-t) = x_{\rm g}(t)$. | *Für das oben skizzierte gerade Zeitsignal gilt: $x_{\rm g}(-t) = x_{\rm g}(t)$. | ||
| Zeile 45: | Zeile 45: | ||
| − | In Formelsammlungen findet man die ''Fourierreihendarstellungen'' beider Signale: | + | In Formelsammlungen findet man die ''Fourierreihendarstellungen'' beider Signale: |
:$$x_{\rm g}(t)=\frac{4}{\pi}\left [ \cos(\omega_0 t)-\frac{1}{3}\cdot \cos(3 \omega_0 t)+\frac{1}{5}\cdot\cos(5 \omega_0 t)- \hspace{0.05cm}\text{...}\hspace{0.05cm} + \hspace{0.05cm}\text{...}\hspace{0.05cm}\right ],$$ | :$$x_{\rm g}(t)=\frac{4}{\pi}\left [ \cos(\omega_0 t)-\frac{1}{3}\cdot \cos(3 \omega_0 t)+\frac{1}{5}\cdot\cos(5 \omega_0 t)- \hspace{0.05cm}\text{...}\hspace{0.05cm} + \hspace{0.05cm}\text{...}\hspace{0.05cm}\right ],$$ | ||
| Zeile 55: | Zeile 55: | ||
:$$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\, {-}\, \hspace{0.05cm}\text{...}\hspace{0.05cm} \, {+} \hspace{0.05cm}\text{...}\hspace{0.05cm}=\frac{\pi}{4}$$ | :$$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\, {-}\, \hspace{0.05cm}\text{...}\hspace{0.05cm} \, {+} \hspace{0.05cm}\text{...}\hspace{0.05cm}=\frac{\pi}{4}$$ | ||
| − | ergeben sich die Amplituden (Maximalwerte) der beiden Rechtecksignale jeweils zu $1$. | + | :ergeben sich die Amplituden (Maximalwerte) der beiden Rechtecksignale jeweils zu $1$. |
*Dies lässt sich auch anhand der Signalverläufe in der obigen Grafik verifizieren: | *Dies lässt sich auch anhand der Signalverläufe in der obigen Grafik verifizieren: | ||
| Zeile 63: | Zeile 63: | ||
==Berechnung der Fourierkoeffizienten== | ==Berechnung der Fourierkoeffizienten== | ||
<br> | <br> | ||
| − | Der Fourierkoeffizient $A_0$ gibt den | + | Der Fourierkoeffizient $A_0$ gibt den $\text{Gleichanteil}$ an, der durch Mittelung über den Signalverlauf $x(t)$ bestimmt werden kann. Aufgrund der Periodizität genügt die Mittelung über eine Periode: |
:$$A_0=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\,{\rm d}t.$$ | :$$A_0=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\,{\rm d}t.$$ | ||
| − | Der Integrationsbereich kann aber auch von $t = 0$ bis $t = T_0$ (oder über eine anders festgelegte gleich lange Periode) gewählt werden. | + | Der Integrationsbereich kann aber auch von $t = 0$ bis $t = T_0$ (oder über eine anders festgelegte gleich lange Periode) gewählt werden. |
| − | Die Bestimmung der Fourierkoeffizienten $A_n$ und $B_n$ $(n \ge 1)$ beruht auf der Eigenschaft, dass die harmonischen Cosinusfunktionen und Sinusfunktionen so genannte [https://de.wikipedia.org/wiki/Orthogonalit%C3%A4t Orthogonalfunktionen] sind. Für diese gilt: | + | Die Bestimmung der Fourierkoeffizienten $A_n$ und $B_n$ $(n \ge 1)$ beruht auf der Eigenschaft, dass die harmonischen Cosinusfunktionen und Sinusfunktionen so genannte [https://de.wikipedia.org/wiki/Orthogonalit%C3%A4t Orthogonalfunktionen] sind. Für diese gilt: |
:$$\int^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\cos(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad falls \it \quad m=n,\atop \rm sonst} \right.$$ | :$$\int^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\cos(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad falls \it \quad m=n,\atop \rm sonst} \right.$$ | ||
| Zeile 78: | Zeile 78: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Fazit:}$ Berücksichtigt man diese Gleichungen, so ergeben sich die Cosinuskoeffizienten $A_n$ und die Sinuskoeffizienten $B_n$ wie folgt: | + | $\text{Fazit:}$ Berücksichtigt man diese Gleichungen, so ergeben sich die $\text{Cosinuskoeffizienten}$ $A_n$ und die $\text{Sinuskoeffizienten}$ $B_n$ wie folgt: |
:$$A_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\cos(n \omega_0 t)\,{\rm d}t,$$ | :$$A_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\cos(n \omega_0 t)\,{\rm d}t,$$ | ||
| Zeile 85: | Zeile 85: | ||
| − | Das Lernvideo [[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|Zur Berechnung der Fourierkoeffizienten]] verdeutlicht diese Gleichungen. | + | Das Lernvideo [[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|Zur Berechnung der Fourierkoeffizienten]] verdeutlicht diese Gleichungen. |
[[Datei:P_ID526__Sig_T_2_4_S2_neu.png|right|frame|Zur Berechnung der Fourierkoeffizienten]] | [[Datei:P_ID526__Sig_T_2_4_S2_neu.png|right|frame|Zur Berechnung der Fourierkoeffizienten]] | ||
| Zeile 94: | Zeile 94: | ||
:$$x(t)=0.4+0.6\cdot \cos(\omega_0 t)-0.3\cdot\sin(3 \omega_0 t).$$ | :$$x(t)=0.4+0.6\cdot \cos(\omega_0 t)-0.3\cdot\sin(3 \omega_0 t).$$ | ||
| − | Da das Integral der Cosinus– und der Sinusfunktion über jeweils eine Periode identisch Null ist, erhält man für den Gleichsignalkoeffizienten $A_0 = 0.4$. | + | Da das Integral der Cosinus– und der Sinusfunktion über jeweils eine Periode identisch Null ist, erhält man für den Gleichsignalkoeffizienten $A_0 = 0.4$. |
| − | + | Die Bestimmungsgleichung für den Cosinuskoeffizienten $A_1$ lautet $($Integrationsbereich von $t = 0$ bis $t = T_0)$: | |
| − | Die Bestimmungsgleichung für den Cosinuskoeffizienten $A_1$ lautet (Integrationsbereich von $t = 0$ bis $t = T_0$ | ||
:$$ \begin{align*} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4\cdot\cos(\omega_0 t)\,{\rm d}t + \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align*} $$ | :$$ \begin{align*} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4\cdot\cos(\omega_0 t)\,{\rm d}t + \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align*} $$ | ||
| − | Das letzte Integral ist aufgrund der Orthogonalität gleich Null; das erste ist ebenfalls Null (Integral über eine Periode). | + | Das letzte Integral ist aufgrund der Orthogonalität gleich Null; das erste ist ebenfalls Null $($Integral über eine Periode$)$. |
| − | *Nur der mittlere Term liefert hier einen Beitrag zu $A_1$, nämlich $2 · 0.6 · 0.5 = 0.6. $ | + | *Nur der mittlere Term liefert hier einen Beitrag zu $A_1$, nämlich $2 · 0.6 · 0.5 = 0.6. $ |
| − | *Bei allen weiteren ($n \ge 2$) Cosinuskoeffizienten liefern alle drei Integrale den Wert Null, und es gilt somit stets $A_{n \hspace{0.05cm}\neq \hspace{0.05cm}1}=0$. | + | *Bei allen weiteren ($n \ge 2$) Cosinuskoeffizienten liefern alle drei Integrale den Wert Null, und es gilt somit stets $A_{n \hspace{0.05cm}\neq \hspace{0.05cm}1}=0$. |
| − | Die Bestimmungsgleichungen für die Sinuskoeffizienten $B_n$ lauten entsprechend: | + | Die Bestimmungsgleichungen für die Sinuskoeffizienten $B_n$ lauten entsprechend: |
:$$ \begin{align*} B_{\it n}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4 \cdot \sin(n \ \omega_0 t)\,{\rm d}t + \frac{2}{T_0} \cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot \cos(\omega_0 t) \sin(n \omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot \sin(3 \omega_0 t) \sin(n \omega_0 t )\,{\rm d}t. \end{align*} $$ | :$$ \begin{align*} B_{\it n}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4 \cdot \sin(n \ \omega_0 t)\,{\rm d}t + \frac{2}{T_0} \cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot \cos(\omega_0 t) \sin(n \omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot \sin(3 \omega_0 t) \sin(n \omega_0 t )\,{\rm d}t. \end{align*} $$ | ||
| − | Für $n \hspace{0.05cm}\neq \hspace{0.05cm}3$ sind alle drei Integralwerte gleich Null und damit gilt auch $B_{n \hspace{0.05cm}\neq \hspace{0.05cm}3} = 0.$ Dagegen liefert für $n=3$ das letzte Integral einen Beitrag, und man erhält für den Sinuskoeffizienten $B_3 = -0.3.$}} | + | *Für $n \hspace{0.05cm}\neq \hspace{0.05cm}3$ sind alle drei Integralwerte gleich Null und damit gilt auch $B_{n \hspace{0.05cm}\neq \hspace{0.05cm}3} = 0.$ |
| + | *Dagegen liefert für $n=3$ das letzte Integral einen Beitrag, und man erhält für den Sinuskoeffizienten $B_3 = -0.3.$}} | ||
==Ausnutzung von Symmetrieeigenschaften== | ==Ausnutzung von Symmetrieeigenschaften== | ||
<br> | <br> | ||
| − | Einige Erkenntnisse über die Fourierkoeffizienten $A_n$ und $B_n$ lassen sich bereits aus den ''Symmetrieeigenschaften'' der Zeitfunktion $x(t)$ ablesen. | + | Einige Erkenntnisse über die Fourierkoeffizienten $A_n$ und $B_n$ lassen sich bereits aus den ''Symmetrieeigenschaften'' der Zeitfunktion $x(t)$ ablesen. |
| − | *Ist das Zeitsignal $x(t)$ eine gerade Funktion ⇒ achsensymmetrisch um die Ordinate $(t = 0)$, so verschwinden alle Sinuskoeffizienten $B_n$, da die Sinusfunktion selbst eine ungerade Funktion ⇒ $\sin(-\alpha) = -\sin(\alpha)$ | + | *Ist das Zeitsignal $x(t)$ eine gerade Funktion ⇒ achsensymmetrisch um die Ordinate $(t = 0)$, so verschwinden alle Sinuskoeffizienten $B_n$, da die Sinusfunktion selbst eine ungerade Funktion ist ⇒ $\sin(-\alpha) = -\sin(\alpha)$: |
| − | :$$B_n = 0 \hspace{0.4cm}(n = 1, 2, 3, \text{...}).$$ | + | :$$B_n = 0 \hspace{0.4cm}(n = 1, \ 2, \ 3, \text{...}).$$ |
| − | *Eine ungerade Funktion $x(t)$ ist punktsymmetrisch um den Koordinatenursprung $(t= 0 | + | *Eine ungerade Funktion $x(t)$ ist punktsymmetrisch um den Koordinatenursprung $(t= 0; \ x =0)$. Deshalb verschwinden hier alle Cosinuskoeffizienten $(A_n = 0)$, da die Cosinusfunktion selbst gerade ist. In diesem Fall ist auch der Gleichanteil $A_0$ stets Null. |
| − | :$$A_n = 0 \hspace{0.4cm}(n = 0, 1, 2, 3, \text{...}).$$ | + | :$$A_n = 0 \hspace{0.4cm}(n = 0, \ 1, \ 2, \ 3, \text{...}).$$ |
| − | *Liegt eine Funktion ohne Gleichanteil vor $(A_0 = 0)$ und ist diese innerhalb einer Periode ungerade ⇒ es gilt $x(t) = -x(t - T_0/2)$, so sind in der Fourierreihendarstellung nur ungerade Vielfache der Grundfrequenz vorhanden. Für die Koeffizienten mit geradzahligem Index gilt dagegen stets: | + | *Liegt eine Funktion ohne Gleichanteil vor $(A_0 = 0)$ und ist diese innerhalb einer Periode ungerade ⇒ es gilt $x(t) = -x(t - T_0/2)$, so sind in der Fourierreihendarstellung nur ungerade Vielfache der Grundfrequenz vorhanden. Für die Koeffizienten mit geradzahligem Index gilt dagegen stets: |
| − | :$$A_n = B_n = 0 \hspace{0.4cm}(n = 2, 4, 6, \text{...}).$$ | + | :$$A_n = B_n = 0 \hspace{0.4cm}(n = 2, \ 4, \ 6, \text{...}).$$ |
| − | *Sind alle Koeffizienten $A_n$ und $B_n$ mit geradzahligem Index $(n = 2, 4, \text{...})$ gleich Null und der Koeffizient $A_0 \neq 0$, so bezieht sich die im letzten Punkt genannte Symmetrieeigenschaft auf den Gleichsignalanteil, und es gilt: | + | *Sind alle Koeffizienten $A_n$ und $B_n$ mit geradzahligem Index $(n = 2, \ 4, \ 6, \text{...})$ gleich Null und der Koeffizient $A_0 \neq 0$, so bezieht sich die im letzten Punkt genannte Symmetrieeigenschaft auf den Gleichsignalanteil, und es gilt: |
:$$x(t) = 2 \cdot A_0 - x (t - T_0/2).$$ | :$$x(t) = 2 \cdot A_0 - x (t - T_0/2).$$ | ||
| − | ''Anmerkung'': Es können auch mehrere | + | ''Anmerkung'': Es können auch mehrere der genannten Symmetrieeigenschaften gleichzeitig erfüllt sein. |
| − | Die Symmetrieeigenschaften der Fourierkoeffizienten werden im ersten Teil des Lernvideos | + | Die Symmetrieeigenschaften der Fourierkoeffizienten werden im ersten Teil des Lernvideos |
| − | [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften und Genauigkeit der Fourierreihe]] zusammenfassend dargestellt. | + | [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften und Genauigkeit der Fourierreihe]] zusammenfassend dargestellt. |
[[Datei:P_ID653__Sig_T_2_4_S3_neu.png|right|frame|Symmetrieeigenschaften der Fourierkoeffizienten]] | [[Datei:P_ID653__Sig_T_2_4_S3_neu.png|right|frame|Symmetrieeigenschaften der Fourierkoeffizienten]] | ||
| Zeile 142: | Zeile 142: | ||
$\text{Beispiel 3:}$ | $\text{Beispiel 3:}$ | ||
Die oben genannten Eigenschaften werden nun an drei Signalverläufen verdeutlicht. | Die oben genannten Eigenschaften werden nun an drei Signalverläufen verdeutlicht. | ||
| − | *$x_1(t)$ ist eine mittelwertbehaftete Funktion ⇒ $A_0 \ne 0$ und zudem gerade | + | *$x_1(t)$ ist eine mittelwertbehaftete Funktion ⇒ $A_0 \ne 0$ und zudem gerade. Sie ist somit ausschließlich durch Cosinuskoeffizienten $A_n$ bestimmt $(B_n = 0)$. |
| − | *Dagegen sind bei der ungeraden Funktion $x_2(t)$ alle $A_n, \ ( n \ge 0)$ identisch Null. | + | *Dagegen sind bei der ungeraden Funktion $x_2(t)$ alle $A_n, \ ( n \ge 0)$ identisch Null. |
| − | *Auch die ungerade Funktion $x_3(t)$ beinhaltet nur Sinuskoeffizienten, aber wegen $x_3(t) = -x_3(t - T_0/2)$ ausschließlich für ungeradzahlige Werte von $n$.}} | + | *Auch die ungerade Funktion $x_3(t)$ beinhaltet nur Sinuskoeffizienten, aber wegen $x_3(t) = -x_3(t - T_0/2)$ ausschließlich für ungeradzahlige Werte von $n$.}} |
==Komplexe Fourierreihe== | ==Komplexe Fourierreihe== | ||
<br> | <br> | ||
| − | Wie auf der Seite [[Signaldarstellung/Harmonische_Schwingung#Darstellung_mit_Cosinus-_und_Sinusanteil|Darstellung mit Cosinus- und Sinusanteil]] für den Fall einer harmonischen Schwingung bereits gezeigt wurde, kann man jedes beliebige periodische Signal | + | Wie auf der Seite [[Signaldarstellung/Harmonische_Schwingung#Darstellung_mit_Cosinus-_und_Sinusanteil|Darstellung mit Cosinus- und Sinusanteil]] für den Fall einer harmonischen Schwingung bereits gezeigt wurde, kann man jedes beliebige periodische Signal |
:$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t)$$ | :$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t)$$ | ||
| Zeile 162: | Zeile 162: | ||
Diese modifizierten Fourierkoeffizienten weisen folgende Eigenschaften auf: | Diese modifizierten Fourierkoeffizienten weisen folgende Eigenschaften auf: | ||
| − | *Der Gleichsignalkoeffizient $C_0$ ist identisch mit $A_0$. | + | *Der $\text{Gleichsignalkoeffizient}$ $C_0$ ist identisch mit $A_0$. |
| − | *Die Betragskoeffizienten lauten mit $n\ge 1$: $C_n = \sqrt{A_n^2 + B_n^2}$. | + | *Die $\text{Betragskoeffizienten}$ lauten mit $n\ge 1$: $C_n = \sqrt{A_n^2 + B_n^2}$. |
| − | *Für die Phasenkoeffizienten gilt: $\varphi_n = \arctan \hspace{0.05cm}(B_n/A_n$). | + | *Für die $\text{Phasenkoeffizienten}$ gilt: $\varphi_n = \arctan \hspace{0.05cm}(B_n/A_n$). |
| − | Mit der „Eulerschen Beziehung” $\cos(x) + {\rm j} \cdot \sin(x) = {\rm e}^{{\rm j} \hspace{0.05cm}x}$ erhält man eine zweite Darstellungsvariante der Fourierreihenentwicklung, die von der komplexen Exponentialfunktion ausgeht. | + | Mit der „Eulerschen Beziehung” $\cos(x) + {\rm j} \cdot \sin(x) = {\rm e}^{{\rm j} \hspace{0.05cm}x}$ erhält man eine zweite Darstellungsvariante der Fourierreihenentwicklung, die von der komplexen Exponentialfunktion ausgeht. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Die | + | Die $\text{komplexe Fourierreihe}$ eines periodischen Signals x(t) lautet wie folgt: |
:$$x(t)=\sum^{+\infty}_{ n=- \infty}D_n\cdot {\rm e}^{ {\rm j} \hspace{0.05cm} n \hspace{0.05cm}\omega_0\hspace{0.05cm} t}.$$ | :$$x(t)=\sum^{+\infty}_{ n=- \infty}D_n\cdot {\rm e}^{ {\rm j} \hspace{0.05cm} n \hspace{0.05cm}\omega_0\hspace{0.05cm} t}.$$ | ||
| + | Hier bezeichnen $D_n$ die $\text{komplexen Fourierkoeffizienten}$, die | ||
| + | *aus den Cosinuskoeffizienten $A_n$ und den Sinuskoeffizienten $B_n$, oder auch | ||
| + | *aus den Betragskoeffizienten $C_n$ sowie den Phasenkoeffizienten $\varphi_n$ | ||
| − | |||
| − | |||
| − | |||
| − | + | wie folgt berechnet werden können $($gültig für $n \neq 0)$: | |
| − | wie folgt berechnet werden können (gültig für $n \neq 0$ | ||
:$$D_n = 1/2\cdot (A_n - {\rm j}\cdot B_n) =1/2\cdot C_n\cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \varphi_n }$$}} | :$$D_n = 1/2\cdot (A_n - {\rm j}\cdot B_n) =1/2\cdot C_n\cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \varphi_n }$$}} | ||
| Zeile 190: | Zeile 189: | ||
:$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t) \cdot{\rm e}^{-\rm j \hspace{0.05cm}\it n \hspace{0.1cm}\omega_{\rm 0} \hspace{0.05cm}t}\, {\rm d}t.$$ | :$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t) \cdot{\rm e}^{-\rm j \hspace{0.05cm}\it n \hspace{0.1cm}\omega_{\rm 0} \hspace{0.05cm}t}\, {\rm d}t.$$ | ||
| − | Solange das Integrationsintervall $T_0$ erhalten bleibt, kann man | + | Solange das Integrationsintervall $T_0$ erhalten bleibt, kann man es ebenso wie bei den Koeffizienten $A_n$ und $B_n$ beliebig verschieben, zum Beispiel von $t = 0$ bis $t = T_0$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Fazit:}$ Der Koeffizient $D_0 | + | $\text{Fazit:}$ Der Koeffizient $D_0 = A_0$ ist stets reell. Für die komplexen Koeffizienten mit negativem Laufindex $(n < 0)$ gilt: |
:$$D_{- n}=D_n^{\hspace{0.05cm}\star} =1/2 \cdot (A_n+ {\rm j}\cdot B_n).$$}} | :$$D_{- n}=D_n^{\hspace{0.05cm}\star} =1/2 \cdot (A_n+ {\rm j}\cdot B_n).$$}} | ||
| Zeile 204: | Zeile 203: | ||
:$$x(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}$$ | :$$x(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}$$ | ||
| − | und dem [[Signaldarstellung/Gesetzm%C3%A4%C3%9Figkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatz]] (für den Frequenzbereich) erhält man für das Spektrum eines periodischen Signals $x(t)$: | + | und dem [[Signaldarstellung/Gesetzm%C3%A4%C3%9Figkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatz]] (für den Frequenzbereich) erhält man für das Spektrum eines periodischen Signals $x(t)$: |
:$$X(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$ | :$$X(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$ | ||
Dies bedeutet: | Dies bedeutet: | ||
| − | *Das Spektrum eines mit $T_0$ periodischen Signals ist ein '''Linienspektrum''' bei ganzzahligen Vielfachen der Grundfrequenz $f_0 = 1/T_0$. | + | *Das Spektrum eines mit $T_0$ periodischen Signals ist ein '''Linienspektrum''' bei ganzzahligen Vielfachen der Grundfrequenz $f_0 = 1/T_0$. |
| − | *Der '''Gleichanteil''' liefert eine Diracfunktion bei $f=0$ mit dem Impulsgewicht $A_0$. | + | *Der '''Gleichanteil''' liefert eine Diracfunktion bei $f=0$ mit dem Impulsgewicht $A_0$. |
| − | *Daneben gibt es '''Diracfunktionen''' $\delta(f \pm n \cdot f_0)$ bei Vielfachen von $f_0$, wobei $\delta(f - n \cdot f_0)$ eine Diracfunktion bei $f= n \cdot f_0$ (also im positiven Frequenzbereich) und $\delta(f + n \cdot f_0)$ eine solche bei der Frequenz $f= -n \cdot f_0$ (im negativen Frequenzbereich) kennzeichnet. | + | *Daneben gibt es '''Diracfunktionen''' $\delta(f \pm n \cdot f_0)$ bei Vielfachen von $f_0$, wobei $\delta(f - n \cdot f_0)$ eine Diracfunktion bei $f= n \cdot f_0$ (also im positiven Frequenzbereich) und $\delta(f + n \cdot f_0)$ eine solche bei der Frequenz $f= -n \cdot f_0$ (im negativen Frequenzbereich) kennzeichnet. |
| − | *Die '''Impulsgewichte''' sind im allgemeinen komplex. | + | *Die '''Impulsgewichte''' sind im allgemeinen komplex. |
| Zeile 219: | Zeile 218: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 4:}$ | $\text{Beispiel 4:}$ | ||
| − | Wir betrachten | + | Wir betrachten wie im [[Signaldarstellung/Fourierreihe#Allgemeine_Beschreibung|$\text{Beispiel 1}$]] zwei periodische Rechtecksignale, jeweils mit Periodendauer $T_0$ und Grundfrequenz $f_0=1/T_0$. Das obere Signal |
| − | |||
:$$x_{\rm g}(t)={4}/{\pi} \cdot \big[\cos(\omega_0 t) - {1}/{3} \cdot \cos(3\omega_0 t)+{1}/{5}\cdot \cos(5\omega_0 t) - \, \text{...} \, + \, \text{...} \big]$$ | :$$x_{\rm g}(t)={4}/{\pi} \cdot \big[\cos(\omega_0 t) - {1}/{3} \cdot \cos(3\omega_0 t)+{1}/{5}\cdot \cos(5\omega_0 t) - \, \text{...} \, + \, \text{...} \big]$$ | ||
| − | + | ist eine gerade, aus verschiedenen Cosinusanteilen zusammengesetzte Funktion. Die zugehörige Spektralfunktion $X_{\rm g}(f)$ ist damit rein reell. | |
| − | + | ''Begründung:'' Wie auf der Seite [[Signaldarstellung/Harmonische_Schwingung#Spektraldarstellung_eines_Cosinussignals|Spektraldarstellung eines Cosinussignals]] bereits beschrieben wurde, liefert die Grundwelle zwei Diracfunktionen bei $\pm f_0$, jeweils gewichtet mit $2/\pi$. | |
| − | *Dieses Gewicht entspricht den (im Allgemeinen komplexen) Fourierkoeffizienten $D_1 = D_{ - 1}^\ast$, die nur im Sonderfall einer geraden Funktion reell sind. | + | *Dieses Gewicht entspricht den (im Allgemeinen komplexen) Fourierkoeffizienten $D_1 = D_{ - 1}^\ast$, die nur im Sonderfall einer geraden Funktion reell sind. |
| − | *Weitere Diracfunktionen gibt es bei $\pm 3f_0$ (negativ), $\pm 5f_0$ (positiv), $\pm 7f_0$ (negativ) usw. | + | *Weitere Diracfunktionen gibt es bei $\pm 3f_0$ (negativ), $\pm 5f_0$ (positiv), $\pm 7f_0$ (negativ) usw. |
| − | *Alle Phasenwerte $\varphi_n$ sind aufgrund der alternierenden Vorzeichen entweder | + | *Alle Phasenwerte $\varphi_n$ sind aufgrund der alternierenden Vorzeichen entweder Null oder $\pi$. |
[[Datei:P_ID528__Sig_T_2_4_S6_neu.png|center|frame|Spektrum eines periodischen Rechtecksignals]] | [[Datei:P_ID528__Sig_T_2_4_S6_neu.png|center|frame|Spektrum eines periodischen Rechtecksignals]] | ||
| − | + | Die unten dargestellte Funktion $x_{\rm u}(t)$ ist ungerade: | |
:$$x_{\rm u}(t)={4}/{\pi} \cdot \big[\sin(\omega_0 t)+{1}/{3} \cdot \sin(3\omega_0 t)+{1}/{5} \cdot \sin(5\omega_0 t)+ \, \text{...}\big].$$ | :$$x_{\rm u}(t)={4}/{\pi} \cdot \big[\sin(\omega_0 t)+{1}/{3} \cdot \sin(3\omega_0 t)+{1}/{5} \cdot \sin(5\omega_0 t)+ \, \text{...}\big].$$ | ||
| − | + | ''Begründung:'' Wie im $\text{Beispiel 4}$ auf der Seite [[Signaldarstellung/Harmonische_Schwingung#Allgemeine_Spektraldarstellung|Allgemeine Spektraldarstellung]] bereits beschrieben wurde, liefert hier die Grundwelle zwei Diracfunktionen bei $+f_0$ $($gewichtet mit $-\text{j}\cdot 2/\pi)$ bzw. bei $-f_0$ $($gewichtet mit $+\text{j}\cdot 2/\pi)$. | |
| − | *Auch alle weiteren Diracfunktionen bei $\pm 3f_0$, $\pm 5f_0$, usw. sind rein imaginär und liegen in gleicher Richtung wie die Diracs bei $\pm f_0$. | + | *Auch alle weiteren Diracfunktionen bei $\pm 3f_0$, $\pm 5f_0$, usw. sind rein imaginär und liegen in gleicher Richtung wie die Diracs bei $\pm f_0$. |
*Die beiden Betragsspektren sind gleich: $\vert X_{\rm u}(f)\vert = \vert X_{\rm g}(f) \vert$.}} | *Die beiden Betragsspektren sind gleich: $\vert X_{\rm u}(f)\vert = \vert X_{\rm g}(f) \vert$.}} | ||
| Zeile 247: | Zeile 245: | ||
==Das Gibbsche Phänomen== | ==Das Gibbsche Phänomen== | ||
<br> | <br> | ||
| − | Nicht jedes Signal eignet sich für die Fourierreihendarstellung. Hier einige Einschränkungen: | + | Nicht jedes Signal eignet sich für die Fourierreihendarstellung. Hier einige Einschränkungen: |
*Eine wichtige Voraussetzung für die Konvergenz der Fourierreihe ist, dass das Signal nur endlich viele Unstetigkeitsstellen je Periode besitzen darf. | *Eine wichtige Voraussetzung für die Konvergenz der Fourierreihe ist, dass das Signal nur endlich viele Unstetigkeitsstellen je Periode besitzen darf. | ||
| − | *An denjenigen Stellen $t=t_i$, an denen $x(t)$ Sprünge aufweist, konvergiert die Reihe gegen den aus dem jeweiligen links– und rechtsseitigen Grenzwert gebildeten arithmetischen Mittelwert. | + | *An denjenigen Stellen $t=t_i$, an denen $x(t)$ Sprünge aufweist, konvergiert die Reihe gegen den aus dem jeweiligen links– und rechtsseitigen Grenzwert gebildeten arithmetischen Mittelwert. |
| − | *In der Umgebung solcher Sprungstellen kommt es in der Reihendarstellung meist zu hochfrequenten Oszillationen. Dieser Fehler ist von prinzipieller Art, das heißt, er ließe sich auch nicht vermeiden, wenn man unendlich viele Summanden berücksichtigen würde. Man spricht vom ''Gibbschen Phänomen'', benannt nach dem Physiker [https://de.wikipedia.org/wiki/Josiah_Willard_Gibbs Josiah Willard Gibbs]. | + | *In der Umgebung solcher Sprungstellen kommt es in der Reihendarstellung meist zu hochfrequenten Oszillationen. Dieser Fehler ist von prinzipieller Art, das heißt, er ließe sich auch nicht vermeiden, wenn man unendlich viele Summanden berücksichtigen würde. Man spricht vom '''Gibbschen Phänomen''', benannt nach dem Physiker [https://de.wikipedia.org/wiki/Josiah_Willard_Gibbs Josiah Willard Gibbs]. |
| − | *Durch eine Erhöhung von $N$ wird zwar der fehlerhafte Bereich kleiner, nicht jedoch die maximale Abweichung zwischen | + | *Durch eine Erhöhung von $N$ wird zwar der fehlerhafte Bereich kleiner, nicht jedoch die maximale Abweichung zwischen $x(t)$ und der Fourierreihendarstellung $x_N(t)$. Der maximale Fehler beträgt ca. $9\%$ der Sprungamplitude – und zwar unabhängig von $N$. |
| − | Das Gibbsche Phänomen und weitere interessante Aspekte werden im Lernvideo | + | Das Gibbsche Phänomen und weitere interessante Aspekte zu vergleichbaren Effekten werden im Lernvideo |
| − | [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]] behandelt. | + | [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]] behandelt. |
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 5:}$ | $\text{Beispiel 5:}$ | ||
| − | In der linken Grafik sehen Sie gepunktet einen Ausschnitt eines periodischen $\pm 1$–Rechtecksignals und die dazugehörige Fourierreihendarstellung mit $N = 1$ (blau), $N = 3$ (rot) und $N = 5$ (grün) Summanden. | + | In der linken Grafik sehen Sie gepunktet einen Ausschnitt eines periodischen $\pm 1$–Rechtecksignals und die dazugehörige Fourierreihendarstellung mit $N = 1$ (blau), $N = 3$ (rot) und $N = 5$ (grün) Summanden. |
| − | *Die Grundwelle hat hier den Amplitudenwert $4/\pi \approx 1.27$. | + | [[Datei:P_ID2720__Sig_T_2_4_S7_neu.png|right|frame|Zum Gibbschen Phänomen]] |
| − | *Auch mit $N = 5$ (das bedeutet wegen $A_2 | + | |
| − | + | *Die Grundwelle hat hier den Amplitudenwert $4/\pi \approx 1.27$. | |
| + | *Auch mit $N = 5$ (das bedeutet wegen $A_2 = A_4 = 0$ drei „relevante” Summanden) unterscheidet sich die Fourierreihe vom anzunähernden Rechtecksignal noch deutlich, vor allem im Bereich der Flanke. | ||
| − | |||
| − | Aus der rechten Grafik ist zu erkennen, dass die Flanke und der innere Bereich mit | + | Aus der rechten Grafik ist zu erkennen, dass die Flanke und der innere Bereich mit |
| − | $N = 100$ relativ gut nachgebildet werden, es aber an | + | $N = 100$ relativ gut nachgebildet werden, es aber an den Sprungstellen aufgrund des Gibbschen Phänomens noch immer zu Überschwingern um $9\%$ kommt. |
| − | *Da hier die Sprungamplituden jeweils gleich $2$ sind, ergeben sich die Maximalwerte näherungsweise zu $1.18$. | + | *Da hier die Sprungamplituden jeweils gleich $2$ sind, ergeben sich die Maximalwerte näherungsweise zu $1.18$. |
| − | *Mit $N = 1000$ wären die Überschwinger genau so groß, aber auf einen noch engeren Raum begrenzt und bei zeitdiskreter Darstellung eventuell nicht zu erkennen.}} | + | *Mit $N = 1000$ wären die Überschwinger genau so groß, aber auf einen noch engeren Raum begrenzt und bei zeitdiskreter Darstellung eventuell nicht mehr zu erkennen.}} |
Aktuelle Version vom 14. April 2021, 11:14 Uhr
Inhaltsverzeichnis
Allgemeine Beschreibung
Jede periodische Funktion $x(t)$ kann in allen Bereichen, in denen sie stetig ist oder nur endlich viele Sprungstellen aufweist, in eine trigonometrische Reihe entwickelt werden, die man als Fourierreihe bezeichnet.
$\text{Definition:}$ Die $\text{Fourierreihe}$ eines periodischen Signals $x(t)$ lautet wie folgt:
- $$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t).$$
Hierbei bezeichnen:
- $A_0$ den $\text{Gleichanteil}$ von $x(t)$,
- $A_n$ die $\text{Cosinuskoeffizienten}$ mit $n \ge 1$,
- $B_n$ die $\text{Sinuskoeffizienten}$ mit $n \ge 1$,
- $\omega_0 = 2\pi/T_0$ die $\text{Grundkreisfrequenz}$ des periodischen Signals $(T_0$ ist die Periodendauer$)$.
Soll die Fourierreihe mit dem tatsächlichen periodischen Signal $x(t)$ exakt übereinstimmen, so müssen im Allgemeinen unendlich viele Cosinus– und Sinuskoeffizienten zur Berechnung herangezogen werden.
- Bricht man die Fourierreihe ab und verwendet jeweils nur $N$ Koeffizienten $A_n$ und $B_n$, so ergibt sich bis auf einige Sonderfälle ein etwas anderer Funktionsverlauf:
- $$x_ N(t) =A_0+\sum^N_{n=1}A_ n \cdot \cos(n \omega_0 t)+\sum^N_{n=1} B_{n} \cdot \sin(n \omega_0 t).$$
- Zwischen dem periodischen Signal $x(t)$ und der Fourierreihenapproximation $x_N(t)$ gilt der Zusammenhang:
- $$x(t)=\lim_{N\to \infty} x_{N}(t).$$
- Ist $N \cdot f_0$ die höchste im Signal $x(t)$ vorkommende Frequenz, so gilt natürlich $x_N(t) = x(t)$.
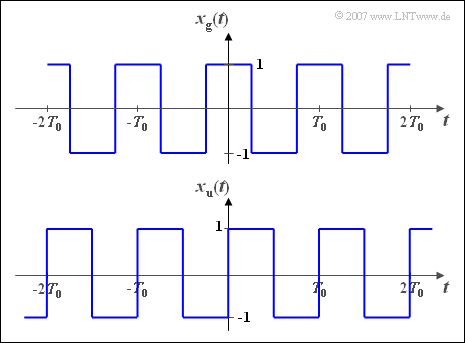
$\text{Beispiel 1:}$ Wir betrachten zwei periodische Rechtecksignale, jeweils mit der Periodendauer $T_0$ und der Grundkreisfrequenz $\omega_0 = 2\pi/T_0$.
- Für das oben skizzierte gerade Zeitsignal gilt: $x_{\rm g}(-t) = x_{\rm g}(t)$.
- Dagegen ist die unten dargestellte Funktion ungerade: $x_{\rm u}(-t) = -x_{\rm u}(t)$.
In Formelsammlungen findet man die Fourierreihendarstellungen beider Signale:
- $$x_{\rm g}(t)=\frac{4}{\pi}\left [ \cos(\omega_0 t)-\frac{1}{3}\cdot \cos(3 \omega_0 t)+\frac{1}{5}\cdot\cos(5 \omega_0 t)- \hspace{0.05cm}\text{...}\hspace{0.05cm} + \hspace{0.05cm}\text{...}\hspace{0.05cm}\right ],$$
- $$x_{\rm u}(t)=\frac{4}{\pi}\left [ \sin(\omega_0 t)+\frac{1}{3}\cdot\sin(3 \omega_0 t)+\frac{1}{5}\cdot\sin(5 \omega_0 t)+ \hspace{0.05cm}\text{...}\hspace{0.05cm} + \hspace{0.05cm}\text{...}\hspace{0.05cm} \right ].$$
- Wegen der allgemeingültigen Beziehung
- $$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\, {-}\, \hspace{0.05cm}\text{...}\hspace{0.05cm} \, {+} \hspace{0.05cm}\text{...}\hspace{0.05cm}=\frac{\pi}{4}$$
- ergeben sich die Amplituden (Maximalwerte) der beiden Rechtecksignale jeweils zu $1$.
- Dies lässt sich auch anhand der Signalverläufe in der obigen Grafik verifizieren:
- $$x_{\rm g}(t = 0) = x_{\rm u}(t = T_0/4) = 1.$$
Berechnung der Fourierkoeffizienten
Der Fourierkoeffizient $A_0$ gibt den $\text{Gleichanteil}$ an, der durch Mittelung über den Signalverlauf $x(t)$ bestimmt werden kann. Aufgrund der Periodizität genügt die Mittelung über eine Periode:
- $$A_0=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\,{\rm d}t.$$
Der Integrationsbereich kann aber auch von $t = 0$ bis $t = T_0$ (oder über eine anders festgelegte gleich lange Periode) gewählt werden.
Die Bestimmung der Fourierkoeffizienten $A_n$ und $B_n$ $(n \ge 1)$ beruht auf der Eigenschaft, dass die harmonischen Cosinusfunktionen und Sinusfunktionen so genannte Orthogonalfunktionen sind. Für diese gilt:
- $$\int^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\cos(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad falls \it \quad m=n,\atop \rm sonst} \right.$$
- $$\int ^{+T_0/2}_{-T_0/2}\sin(n\omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad falls \it \quad m=n,\atop \rm sonst} \right.$$
- $$\int ^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=0 \quad \rm f\ddot{u}r\quad alle \ \it m, \ n.$$
$\text{Fazit:}$ Berücksichtigt man diese Gleichungen, so ergeben sich die $\text{Cosinuskoeffizienten}$ $A_n$ und die $\text{Sinuskoeffizienten}$ $B_n$ wie folgt:
- $$A_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\cos(n \omega_0 t)\,{\rm d}t,$$
- $$B_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\sin(n \omega_0 t)\,{\rm d}t.$$
Das Lernvideo Zur Berechnung der Fourierkoeffizienten verdeutlicht diese Gleichungen.
$\text{Beispiel 2:}$ Wir betrachten die gezeichnete periodische Zeitfunktion
- $$x(t)=0.4+0.6\cdot \cos(\omega_0 t)-0.3\cdot\sin(3 \omega_0 t).$$
Da das Integral der Cosinus– und der Sinusfunktion über jeweils eine Periode identisch Null ist, erhält man für den Gleichsignalkoeffizienten $A_0 = 0.4$.
Die Bestimmungsgleichung für den Cosinuskoeffizienten $A_1$ lautet $($Integrationsbereich von $t = 0$ bis $t = T_0)$:
- $$ \begin{align*} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4\cdot\cos(\omega_0 t)\,{\rm d}t + \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align*} $$
Das letzte Integral ist aufgrund der Orthogonalität gleich Null; das erste ist ebenfalls Null $($Integral über eine Periode$)$.
- Nur der mittlere Term liefert hier einen Beitrag zu $A_1$, nämlich $2 · 0.6 · 0.5 = 0.6. $
- Bei allen weiteren ($n \ge 2$) Cosinuskoeffizienten liefern alle drei Integrale den Wert Null, und es gilt somit stets $A_{n \hspace{0.05cm}\neq \hspace{0.05cm}1}=0$.
Die Bestimmungsgleichungen für die Sinuskoeffizienten $B_n$ lauten entsprechend:
- $$ \begin{align*} B_{\it n}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4 \cdot \sin(n \ \omega_0 t)\,{\rm d}t + \frac{2}{T_0} \cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot \cos(\omega_0 t) \sin(n \omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot \sin(3 \omega_0 t) \sin(n \omega_0 t )\,{\rm d}t. \end{align*} $$
- Für $n \hspace{0.05cm}\neq \hspace{0.05cm}3$ sind alle drei Integralwerte gleich Null und damit gilt auch $B_{n \hspace{0.05cm}\neq \hspace{0.05cm}3} = 0.$
- Dagegen liefert für $n=3$ das letzte Integral einen Beitrag, und man erhält für den Sinuskoeffizienten $B_3 = -0.3.$
Ausnutzung von Symmetrieeigenschaften
Einige Erkenntnisse über die Fourierkoeffizienten $A_n$ und $B_n$ lassen sich bereits aus den Symmetrieeigenschaften der Zeitfunktion $x(t)$ ablesen.
- Ist das Zeitsignal $x(t)$ eine gerade Funktion ⇒ achsensymmetrisch um die Ordinate $(t = 0)$, so verschwinden alle Sinuskoeffizienten $B_n$, da die Sinusfunktion selbst eine ungerade Funktion ist ⇒ $\sin(-\alpha) = -\sin(\alpha)$:
- $$B_n = 0 \hspace{0.4cm}(n = 1, \ 2, \ 3, \text{...}).$$
- Eine ungerade Funktion $x(t)$ ist punktsymmetrisch um den Koordinatenursprung $(t= 0; \ x =0)$. Deshalb verschwinden hier alle Cosinuskoeffizienten $(A_n = 0)$, da die Cosinusfunktion selbst gerade ist. In diesem Fall ist auch der Gleichanteil $A_0$ stets Null.
- $$A_n = 0 \hspace{0.4cm}(n = 0, \ 1, \ 2, \ 3, \text{...}).$$
- Liegt eine Funktion ohne Gleichanteil vor $(A_0 = 0)$ und ist diese innerhalb einer Periode ungerade ⇒ es gilt $x(t) = -x(t - T_0/2)$, so sind in der Fourierreihendarstellung nur ungerade Vielfache der Grundfrequenz vorhanden. Für die Koeffizienten mit geradzahligem Index gilt dagegen stets:
- $$A_n = B_n = 0 \hspace{0.4cm}(n = 2, \ 4, \ 6, \text{...}).$$
- Sind alle Koeffizienten $A_n$ und $B_n$ mit geradzahligem Index $(n = 2, \ 4, \ 6, \text{...})$ gleich Null und der Koeffizient $A_0 \neq 0$, so bezieht sich die im letzten Punkt genannte Symmetrieeigenschaft auf den Gleichsignalanteil, und es gilt:
- $$x(t) = 2 \cdot A_0 - x (t - T_0/2).$$
Anmerkung: Es können auch mehrere der genannten Symmetrieeigenschaften gleichzeitig erfüllt sein.
Die Symmetrieeigenschaften der Fourierkoeffizienten werden im ersten Teil des Lernvideos Eigenschaften und Genauigkeit der Fourierreihe zusammenfassend dargestellt.
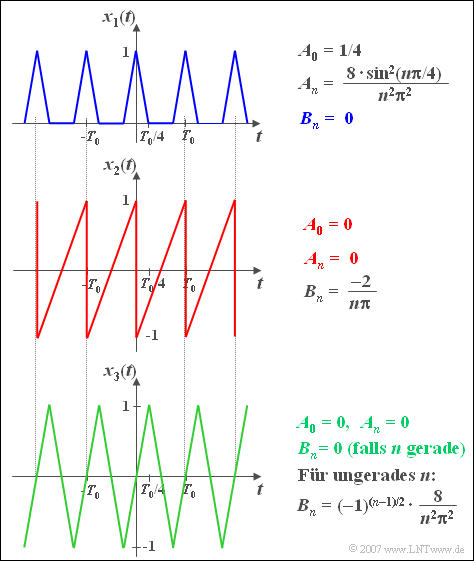
$\text{Beispiel 3:}$ Die oben genannten Eigenschaften werden nun an drei Signalverläufen verdeutlicht.
- $x_1(t)$ ist eine mittelwertbehaftete Funktion ⇒ $A_0 \ne 0$ und zudem gerade. Sie ist somit ausschließlich durch Cosinuskoeffizienten $A_n$ bestimmt $(B_n = 0)$.
- Dagegen sind bei der ungeraden Funktion $x_2(t)$ alle $A_n, \ ( n \ge 0)$ identisch Null.
- Auch die ungerade Funktion $x_3(t)$ beinhaltet nur Sinuskoeffizienten, aber wegen $x_3(t) = -x_3(t - T_0/2)$ ausschließlich für ungeradzahlige Werte von $n$.
Komplexe Fourierreihe
Wie auf der Seite Darstellung mit Cosinus- und Sinusanteil für den Fall einer harmonischen Schwingung bereits gezeigt wurde, kann man jedes beliebige periodische Signal
- $$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t)$$
auch mit Hilfe der Betrags- und Phasenkoeffizienten darstellen:
- $$x(t) =C_0+\sum^{\infty}_{n=1}C_{\it n} \cdot\cos(n \omega_0 t-\varphi_n).$$
Diese modifizierten Fourierkoeffizienten weisen folgende Eigenschaften auf:
- Der $\text{Gleichsignalkoeffizient}$ $C_0$ ist identisch mit $A_0$.
- Die $\text{Betragskoeffizienten}$ lauten mit $n\ge 1$: $C_n = \sqrt{A_n^2 + B_n^2}$.
- Für die $\text{Phasenkoeffizienten}$ gilt: $\varphi_n = \arctan \hspace{0.05cm}(B_n/A_n$).
Mit der „Eulerschen Beziehung” $\cos(x) + {\rm j} \cdot \sin(x) = {\rm e}^{{\rm j} \hspace{0.05cm}x}$ erhält man eine zweite Darstellungsvariante der Fourierreihenentwicklung, die von der komplexen Exponentialfunktion ausgeht.
$\text{Definition:}$ Die $\text{komplexe Fourierreihe}$ eines periodischen Signals x(t) lautet wie folgt:
- $$x(t)=\sum^{+\infty}_{ n=- \infty}D_n\cdot {\rm e}^{ {\rm j} \hspace{0.05cm} n \hspace{0.05cm}\omega_0\hspace{0.05cm} t}.$$
Hier bezeichnen $D_n$ die $\text{komplexen Fourierkoeffizienten}$, die
- aus den Cosinuskoeffizienten $A_n$ und den Sinuskoeffizienten $B_n$, oder auch
- aus den Betragskoeffizienten $C_n$ sowie den Phasenkoeffizienten $\varphi_n$
wie folgt berechnet werden können $($gültig für $n \neq 0)$:
- $$D_n = 1/2\cdot (A_n - {\rm j}\cdot B_n) =1/2\cdot C_n\cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \varphi_n }$$
Die komplexen Fourierkoeffizienten kann man nach folgender Gleichung auch direkt berechnen:
- $$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t) \cdot{\rm e}^{-\rm j \hspace{0.05cm}\it n \hspace{0.1cm}\omega_{\rm 0} \hspace{0.05cm}t}\, {\rm d}t.$$
Solange das Integrationsintervall $T_0$ erhalten bleibt, kann man es ebenso wie bei den Koeffizienten $A_n$ und $B_n$ beliebig verschieben, zum Beispiel von $t = 0$ bis $t = T_0$.
$\text{Fazit:}$ Der Koeffizient $D_0 = A_0$ ist stets reell. Für die komplexen Koeffizienten mit negativem Laufindex $(n < 0)$ gilt:
- $$D_{- n}=D_n^{\hspace{0.05cm}\star} =1/2 \cdot (A_n+ {\rm j}\cdot B_n).$$
Spektrum eines periodischen Signals
Ausgehend von der gerade hergeleiteten komplexen Fourierreihe
- $$x(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}$$
und dem Verschiebungssatz (für den Frequenzbereich) erhält man für das Spektrum eines periodischen Signals $x(t)$:
- $$X(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$
Dies bedeutet:
- Das Spektrum eines mit $T_0$ periodischen Signals ist ein Linienspektrum bei ganzzahligen Vielfachen der Grundfrequenz $f_0 = 1/T_0$.
- Der Gleichanteil liefert eine Diracfunktion bei $f=0$ mit dem Impulsgewicht $A_0$.
- Daneben gibt es Diracfunktionen $\delta(f \pm n \cdot f_0)$ bei Vielfachen von $f_0$, wobei $\delta(f - n \cdot f_0)$ eine Diracfunktion bei $f= n \cdot f_0$ (also im positiven Frequenzbereich) und $\delta(f + n \cdot f_0)$ eine solche bei der Frequenz $f= -n \cdot f_0$ (im negativen Frequenzbereich) kennzeichnet.
- Die Impulsgewichte sind im allgemeinen komplex.
Diese Aussagen werden nun anhand zweier Beispiele verdeutlicht.
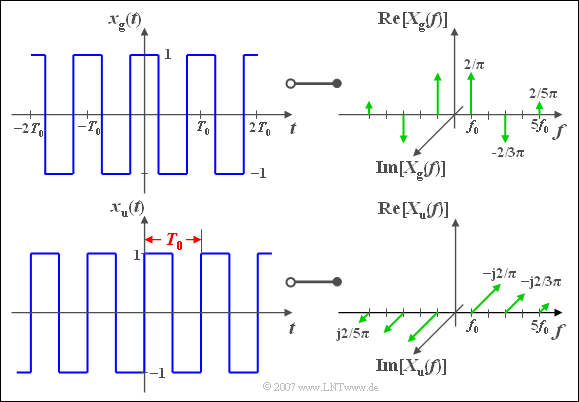
$\text{Beispiel 4:}$ Wir betrachten wie im $\text{Beispiel 1}$ zwei periodische Rechtecksignale, jeweils mit Periodendauer $T_0$ und Grundfrequenz $f_0=1/T_0$. Das obere Signal
- $$x_{\rm g}(t)={4}/{\pi} \cdot \big[\cos(\omega_0 t) - {1}/{3} \cdot \cos(3\omega_0 t)+{1}/{5}\cdot \cos(5\omega_0 t) - \, \text{...} \, + \, \text{...} \big]$$
ist eine gerade, aus verschiedenen Cosinusanteilen zusammengesetzte Funktion. Die zugehörige Spektralfunktion $X_{\rm g}(f)$ ist damit rein reell.
Begründung: Wie auf der Seite Spektraldarstellung eines Cosinussignals bereits beschrieben wurde, liefert die Grundwelle zwei Diracfunktionen bei $\pm f_0$, jeweils gewichtet mit $2/\pi$.
- Dieses Gewicht entspricht den (im Allgemeinen komplexen) Fourierkoeffizienten $D_1 = D_{ - 1}^\ast$, die nur im Sonderfall einer geraden Funktion reell sind.
- Weitere Diracfunktionen gibt es bei $\pm 3f_0$ (negativ), $\pm 5f_0$ (positiv), $\pm 7f_0$ (negativ) usw.
- Alle Phasenwerte $\varphi_n$ sind aufgrund der alternierenden Vorzeichen entweder Null oder $\pi$.
Die unten dargestellte Funktion $x_{\rm u}(t)$ ist ungerade:
- $$x_{\rm u}(t)={4}/{\pi} \cdot \big[\sin(\omega_0 t)+{1}/{3} \cdot \sin(3\omega_0 t)+{1}/{5} \cdot \sin(5\omega_0 t)+ \, \text{...}\big].$$
Begründung: Wie im $\text{Beispiel 4}$ auf der Seite Allgemeine Spektraldarstellung bereits beschrieben wurde, liefert hier die Grundwelle zwei Diracfunktionen bei $+f_0$ $($gewichtet mit $-\text{j}\cdot 2/\pi)$ bzw. bei $-f_0$ $($gewichtet mit $+\text{j}\cdot 2/\pi)$.
- Auch alle weiteren Diracfunktionen bei $\pm 3f_0$, $\pm 5f_0$, usw. sind rein imaginär und liegen in gleicher Richtung wie die Diracs bei $\pm f_0$.
- Die beiden Betragsspektren sind gleich: $\vert X_{\rm u}(f)\vert = \vert X_{\rm g}(f) \vert$.
Das Gibbsche Phänomen
Nicht jedes Signal eignet sich für die Fourierreihendarstellung. Hier einige Einschränkungen:
- Eine wichtige Voraussetzung für die Konvergenz der Fourierreihe ist, dass das Signal nur endlich viele Unstetigkeitsstellen je Periode besitzen darf.
- An denjenigen Stellen $t=t_i$, an denen $x(t)$ Sprünge aufweist, konvergiert die Reihe gegen den aus dem jeweiligen links– und rechtsseitigen Grenzwert gebildeten arithmetischen Mittelwert.
- In der Umgebung solcher Sprungstellen kommt es in der Reihendarstellung meist zu hochfrequenten Oszillationen. Dieser Fehler ist von prinzipieller Art, das heißt, er ließe sich auch nicht vermeiden, wenn man unendlich viele Summanden berücksichtigen würde. Man spricht vom Gibbschen Phänomen, benannt nach dem Physiker Josiah Willard Gibbs.
- Durch eine Erhöhung von $N$ wird zwar der fehlerhafte Bereich kleiner, nicht jedoch die maximale Abweichung zwischen $x(t)$ und der Fourierreihendarstellung $x_N(t)$. Der maximale Fehler beträgt ca. $9\%$ der Sprungamplitude – und zwar unabhängig von $N$.
Das Gibbsche Phänomen und weitere interessante Aspekte zu vergleichbaren Effekten werden im Lernvideo
Eigenschaften der Fourierreihendarstellung behandelt.
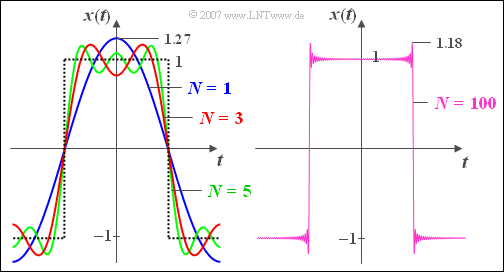
$\text{Beispiel 5:}$ In der linken Grafik sehen Sie gepunktet einen Ausschnitt eines periodischen $\pm 1$–Rechtecksignals und die dazugehörige Fourierreihendarstellung mit $N = 1$ (blau), $N = 3$ (rot) und $N = 5$ (grün) Summanden.
- Die Grundwelle hat hier den Amplitudenwert $4/\pi \approx 1.27$.
- Auch mit $N = 5$ (das bedeutet wegen $A_2 = A_4 = 0$ drei „relevante” Summanden) unterscheidet sich die Fourierreihe vom anzunähernden Rechtecksignal noch deutlich, vor allem im Bereich der Flanke.
Aus der rechten Grafik ist zu erkennen, dass die Flanke und der innere Bereich mit
$N = 100$ relativ gut nachgebildet werden, es aber an den Sprungstellen aufgrund des Gibbschen Phänomens noch immer zu Überschwingern um $9\%$ kommt.
- Da hier die Sprungamplituden jeweils gleich $2$ sind, ergeben sich die Maximalwerte näherungsweise zu $1.18$.
- Mit $N = 1000$ wären die Überschwinger genau so groß, aber auf einen noch engeren Raum begrenzt und bei zeitdiskreter Darstellung eventuell nicht mehr zu erkennen.
Aufgaben zum Kapitel
Aufgabe 2.4: Gleichgerichteter Cosinus
Aufgabe 2.5: Einweggleichrichtung
Aufgabe 2.6: Komplexe Fourierreihe
Aufgabe 2.6Z: Betrag und Phase