Kanalcodierung/Decodierung linearer Blockcodes: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
== Blockschaltbild und Voraussetzungen == | == Blockschaltbild und Voraussetzungen == | ||
<br> | <br> | ||
| − | Wir gehen von dem bereits im Kapitel [[Kanalcodierung/Kanalmodelle_und Entscheiderstrukturen|Kanalmodelle und Entscheiderstrukturen]] gezeigten Blockschaltbild aus, wobei als Kanalmodell meist der | + | Wir gehen von dem bereits im Kapitel [[Kanalcodierung/Kanalmodelle_und Entscheiderstrukturen|"Kanalmodelle und Entscheiderstrukturen"]] gezeigten Blockschaltbild aus, wobei als Kanalmodell meist der "Binary Symmetric Channel" $\rm (BSC)$ verwendet wird. Zur Codewortschätzung verwenden wir den "Maximum–Likelihood–Entscheider" $\rm (ML)$, der für binäre Codes ⇒ $\underline{x} \in {\rm GF}(2^n)$ auf Blockebene das gleiche Ergebnis liefert wie der [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Definitionen_der_verschiedenen_Optimalempf.C3.A4nger|"MAP–Empfänger"]].<br> |
[[Datei:P ID2360 KC T 1 5 S1 v2.png|center|frame|Blockschaltbild zur Decodierung von Blockcodes|class=fit]] | [[Datei:P ID2360 KC T 1 5 S1 v2.png|center|frame|Blockschaltbild zur Decodierung von Blockcodes|class=fit]] | ||
Die Aufgabe des Kanaldecoders kann wie folgt beschrieben werden: | Die Aufgabe des Kanaldecoders kann wie folgt beschrieben werden: | ||
| − | *Der Vektor $\underline{v}$ nach der Decodierung (an der Sinke) soll möglichst gut mit dem Informationswort $\underline{u}$ übereinstimmen. Das heißt: Die '''Blockfehlerwahrscheinlichkeit''' soll möglichst klein sein: | + | *Der Vektor $\underline{v}$ nach der Decodierung (an der Sinke) soll möglichst gut mit dem Informationswort $\underline{u}$ übereinstimmen. <br>Das heißt: Die '''Blockfehlerwahrscheinlichkeit''' soll möglichst klein sein: |
::<math>{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.</math> | ::<math>{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.</math> | ||
| − | *Aufgrund der deterministischen Zuweisungen $\underline{x} = {\rm enc}(\underline{u})$ bzw. $\underline{v} = {\rm enc}^{-1}(\underline{z})$ gilt aber auch: | + | *Aufgrund der deterministischen Zuweisungen $\underline{x} = {\rm enc}(\underline{u})$ bzw. $\underline{v} = {\rm enc}^{-1}(\underline{z})$ gilt aber auch: |
::<math>{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{z} \ne \underline{x}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.</math> | ::<math>{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{z} \ne \underline{x}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.</math> | ||
| − | *Gesucht ist somit das zum gegebenen Empfangswort $\underline{y} = \underline{x} +\underline{e}$ am wahrscheinlichsten gesendete Codewort $\underline{x}_i$, das als Ergebnis $\underline{z}$ weiter gegeben wird: | + | *Gesucht ist somit das zum gegebenen Empfangswort $\underline{y} = \underline{x} +\underline{e}$ am wahrscheinlichsten gesendete Codewort $\underline{x}_i$, das als Ergebnis $\underline{z}$ weiter gegeben wird: |
::<math>\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.</math> | ::<math>\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.</math> | ||
| − | *Beim BSC–Kanal gilt sowohl $\underline{x}_i \in {\rm GF}(2^n)$ als auch $\underline{y} \in {\rm GF}(2^n)$, so dass die Maximum–Likelihood–Regel auch mit der [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung |Hamming–Distanz]] $d_{\rm H}( \underline{y}, \, \underline{x}_i)$ geschrieben werden kann: | + | *Beim BSC–Kanal gilt sowohl $\underline{x}_i \in {\rm GF}(2^n)$ als auch $\underline{y} \in {\rm GF}(2^n)$, so dass die Maximum–Likelihood–Regel auch mit der [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung |Hamming–Distanz]] $d_{\rm H}( \underline{y}, \, \underline{x}_i)$ geschrieben werden kann: |
::<math>\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ::<math>\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ||
| Zeile 32: | Zeile 32: | ||
== Prinzip der Syndromdecodierung == | == Prinzip der Syndromdecodierung == | ||
<br> | <br> | ||
| − | Vorausgesetzt wird hier ein $(n, \, k)$–Blockcode mit der Prüfmatrix $\boldsymbol{\rm H}$ und den systematischen Codeworten | + | Vorausgesetzt wird hier ein $(n, \, k)$–Blockcode mit der Prüfmatrix $\boldsymbol{\rm H}$ und den systematischen Codeworten |
::<math>\underline{x}\hspace{0.05cm} = (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) | ::<math>\underline{x}\hspace{0.05cm} = (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) | ||
= (u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k, p_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, p_{n-k})\hspace{0.05cm}. </math> | = (u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k, p_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, p_{n-k})\hspace{0.05cm}. </math> | ||
| − | Mit dem Fehlervektor $\underline{e}$ gilt dann für das Empfangswort: | + | Mit dem Fehlervektor $\underline{e}$ gilt dann für das Empfangswort: |
::<math>\underline{y} = \underline{x} + \underline{e} \hspace{0.05cm}, \hspace{0.4cm} \underline{y} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{x} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{e} \in \hspace{0.1cm} {\rm GF}(2^n) | ::<math>\underline{y} = \underline{x} + \underline{e} \hspace{0.05cm}, \hspace{0.4cm} \underline{y} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{x} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{e} \in \hspace{0.1cm} {\rm GF}(2^n) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Ein Bitfehler an der Position $i$, das heißt $y_i ≠ x_i$, wird ausgedrückt durch den Fehlerkoeffizienten $e_i = 1$.<br> | + | Ein Bitfehler an der Position $i$, das heißt $y_i ≠ x_i$, wird ausgedrückt durch den Fehlerkoeffizienten $e_i = 1$.<br> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Das '''Syndrom''' $\underline{s} = (s_0, s_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, s_{m-1})$ berechnet sich (als Zeilen– bzw. Spaltenvektor) aus dem Empfangswort $\underline{y}$ und der Prüfmatrix $\boldsymbol{\rm H}$ | + | $\text{Definition:}$ Das '''Syndrom''' $\underline{s} = (s_0, s_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, s_{m-1})$ berechnet sich (als Zeilen– bzw. Spaltenvektor) aus dem Empfangswort $\underline{y}$ und der Prüfmatrix $\boldsymbol{\rm H}$ wie folgt: |
::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T}\hspace{0.3cm}{\rm bzw.}\hspace{0.3cm} | ::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T}\hspace{0.3cm}{\rm bzw.}\hspace{0.3cm} | ||
\underline{s}^{\rm T} = { \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T}\hspace{0.05cm}.</math> | \underline{s}^{\rm T} = { \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T}\hspace{0.05cm}.</math> | ||
| − | Die Vektorlänge von $\underline{s}$ ist gleich $m = n-k$ (Zeilenzahl von $\boldsymbol{\rm H}$ | + | Die Vektorlänge von $\underline{s}$ ist gleich $m = n-k$ $($Zeilenzahl von $\boldsymbol{\rm H})$.}}<br> |
| − | Das Syndrom $\underline{s}$ zeigt folgende Charakteristika: | + | Das Syndrom $\underline{s}$ zeigt folgende Charakteristika: |
| − | *Wegen der Gleichung $\underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{0}$ hängt das Syndrom $\underline{s}$ nicht vom Codewort $\underline{x}$ ab, sondern allein vom Fehlervektor $\underline{e}$: | + | *Wegen der Gleichung $\underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{0}$ hängt das Syndrom $\underline{s}$ nicht vom Codewort $\underline{x}$ ab, sondern allein vom Fehlervektor $\underline{e}$: |
::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} | ::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} | ||
| Zeile 60: | Zeile 60: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Bei hinreichend wenig Bitfehlern liefert $\underline{s}$ einen eindeutigen Hinweis auf die Fehlerpositionen und ermöglicht so eine vollständige Fehlerkorrektur.<br><br> | + | *Bei hinreichend wenig Bitfehlern liefert $\underline{s}$ einen eindeutigen Hinweis auf die Fehlerpositionen und ermöglicht so eine vollständige Fehlerkorrektur.<br><br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 1:}$ Ausgehend vom systematischen [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Einige_Eigenschaften_des_.287.2C_4.2C_3.29.E2.80.93Hamming.E2.80.93Codes|$\text{(7, 4, 3)}$–Hamming–Code]] erhält man für den Empfangsvektor $\underline{y} = (0, 1, 1, 1, 0, 0, 1)$ das folgende Ergebnis: | + | $\text{Beispiel 1:}$ Ausgehend vom systematischen [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Einige_Eigenschaften_des_.287.2C_4.2C_3.29.E2.80.93Hamming.E2.80.93Codes|$\text{(7, 4, 3)}$–Hamming–Code]] erhält man für den Empfangsvektor $\underline{y} = (0, 1, 1, 1, 0, 0, 1)$ das folgende Ergebnis: |
::<math>{ \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T} | ::<math>{ \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T} | ||
| Zeile 84: | Zeile 84: | ||
\end{pmatrix} = \underline{s}^{\rm T} \hspace{0.05cm}.</math> | \end{pmatrix} = \underline{s}^{\rm T} \hspace{0.05cm}.</math> | ||
| − | Vergleicht man das Syndrom mit den [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Codefestlegung_durch_die_Pr.C3.BCfmatrix| Prüfgleichungen]] des Hamming–Codes, so erkennt man, dass | + | Vergleicht man das Syndrom mit den [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Codefestlegung_durch_die_Pr.C3.BCfmatrix| Prüfgleichungen]] des Hamming–Codes, so erkennt man, dass |
| − | *am wahrscheinlichsten das vierte Symbol $(x_4 = u_4)$ des Codewortes verfälscht wurde,<br> | + | *am wahrscheinlichsten das vierte Symbol $(x_4 = u_4)$ des Codewortes verfälscht wurde,<br> |
| − | *der Codewortschätzer somit das Ergebnis $\underline{z} = (0, 1, 1, 0, 0, 0, 1)$ liefern wird | + | *der Codewortschätzer somit das Ergebnis $\underline{z} = (0, 1, 1, 0, 0, 0, 1)$ liefern wird,<br> |
*die Entscheidung nur dann richtig ist, wenn bei der Übertragung nur ein Bit verfälscht wurde.<br><br> | *die Entscheidung nur dann richtig ist, wenn bei der Übertragung nur ein Bit verfälscht wurde.<br><br> | ||
| − | Nachfolgend sind die erforderlichen Korrekturen für den $\text{(7, 4, 3)}$–Hamming–Code angegeben, die sich aus dem errechneten Syndrom $\underline{s}$ entsprechend den Spalten der Prüfmatrix ergeben: | + | Nachfolgend sind die erforderlichen Korrekturen für den $\text{(7, 4, 3)}$–Hamming–Code angegeben, die sich aus dem errechneten Syndrom $\underline{s}$ entsprechend den Spalten der Prüfmatrix ergeben: |
::<math>\underline{s} = (0, 0, 0) \hspace{0.10cm} \Rightarrow\hspace{0.10cm}{\rm keine\hspace{0.15cm} Korrektur}\hspace{0.05cm};\hspace{0.8cm}\underline{s} = (1, 0, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm}p_1{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};</math> | ::<math>\underline{s} = (0, 0, 0) \hspace{0.10cm} \Rightarrow\hspace{0.10cm}{\rm keine\hspace{0.15cm} Korrektur}\hspace{0.05cm};\hspace{0.8cm}\underline{s} = (1, 0, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm}p_1{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};</math> | ||
| Zeile 101: | Zeile 101: | ||
<br> | <br> | ||
Wir gehen weiterhin vom BSC–Kanalmodell aus. Das bedeutet: | Wir gehen weiterhin vom BSC–Kanalmodell aus. Das bedeutet: | ||
| − | *Der Empfangsvektor $\underline{y}$ und der Fehlervektor $\underline{e}$ sind Elemente von ${\rm GF}(2^n)$. | + | *Der Empfangsvektor $\underline{y}$ und der Fehlervektor $\underline{e}$ sind Elemente von ${\rm GF}(2^n)$. |
| − | *Die möglichen Codeworte $\underline{x}_i$ gehören zum Code $\mathcal{C}$, der einen $(n-k)$–dimensionalen Untervektorraum von ${\rm GF}(2^n)$ aufspannt. | + | *Die möglichen Codeworte $\underline{x}_i$ gehören zum Code $\mathcal{C}$, der einen $(n-k)$–dimensionalen Untervektorraum von ${\rm GF}(2^n)$ aufspannt. |
Unter dieser Voraussetzung fassen wir die Ergebnisse der letzten Seiten nochmals kurz zusammen: | Unter dieser Voraussetzung fassen wir die Ergebnisse der letzten Seiten nochmals kurz zusammen: | ||
| − | *Die Syndromdecodierung ist eine Realisierungsmöglichkeit der Maximum–Likelihood–Detektion von Blockcodes. Man entscheidet sich für das Codewort $\underline{x}_i$ mit der geringsten Hamming–Distanz zum Empfangswort $\underline{y}$ : | + | *Die Syndromdecodierung ist eine Realisierungsmöglichkeit der Maximum–Likelihood–Detektion von Blockcodes. Man entscheidet sich für das Codewort $\underline{x}_i$ mit der geringsten Hamming–Distanz zum Empfangswort $\underline{y}$ : |
::<math>\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ::<math>\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ||
d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | ||
| − | *Die Syndromdecodierung ist aber auch die Suche nach dem wahrscheinlichsten Fehlervektor $\underline{e}$, der die Bedingung $\underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{s}$ erfüllt. Das <i>Syndrom</i> liegt dabei durch $\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} $ fest. | + | *Die Syndromdecodierung ist aber auch die Suche nach dem wahrscheinlichsten Fehlervektor $\underline{e}$, der die Bedingung $\underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{s}$ erfüllt. Das <i>Syndrom</i> liegt dabei durch die Gleichung $\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} $ fest. |
| − | *Mit dem [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung| Hamming–Gewicht]] $w_{\rm H}(\underline{e})$ kann die zweite Interpretation auch wie folgt mathematisch formuliert werden: | + | *Mit dem [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung| Hamming–Gewicht]] $w_{\rm H}(\underline{e})$ kann die zweite Interpretation auch wie folgt mathematisch formuliert werden: |
::<math>\underline{z} = \underline{y} + {\rm arg} \min_{\underline{e}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} {\rm GF}(2^n)} \hspace{0.1cm} | ::<math>\underline{z} = \underline{y} + {\rm arg} \min_{\underline{e}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} {\rm GF}(2^n)} \hspace{0.1cm} | ||
| Zeile 119: | Zeile 119: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Fazit:}$ Zu beachten ist, dass der Fehlervektor $\underline{e}$ ebenso wie der Empfangsvektor $\underline{y}$ ein Element von ${\rm GF}(2^n)$ ist im Gegensatz zum Syndrom $\underline{s} \in {\rm GF}(2^m)$ mit der Anzahl $m = n-k$ der Prüfgleichungen. Das bedeutet, | + | $\text{Fazit:}$ Zu beachten ist, dass der Fehlervektor $\underline{e}$ ebenso wie der Empfangsvektor $\underline{y}$ ein Element von ${\rm GF}(2^n)$ ist im Gegensatz zum Syndrom $\underline{s} \in {\rm GF}(2^m)$ mit der Anzahl $m = n-k$ der Prüfgleichungen. Das bedeutet, |
| − | *dass die Zuordnung zwischen Syndrom $\underline{s}$ und Fehlervektor $\underline{e}$ nicht eindeutig ist, sondern<br> | + | *dass die Zuordnung zwischen dem Syndrom $\underline{s}$ und dem Fehlervektor $\underline{e}$ nicht eindeutig ist, sondern<br> |
| − | *dass jeweils $2^k$ Fehlervektoren zum gleichen Syndrom $\underline{s}$ führen, die man zu einer '''Nebenklasse''' (englisch: <i>Coset</i> ) zusammenfasst.}}<br> | + | *dass jeweils $2^k$ Fehlervektoren zum gleichen Syndrom $\underline{s}$ führen, die man zu einer '''Nebenklasse''' (englisch: <i>Coset</i> ) zusammenfasst.}}<br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 2:}$ Der Sachverhalt soll hier am Beispiel $n = 5, k = 2$ ⇒ $m = n-k = 3$ verdeutlicht werden. | + | $\text{Beispiel 2:}$ Der Sachverhalt soll hier am Beispiel $n = 5, \ k = 2$ ⇒ $m = n-k = 3$ verdeutlicht werden. |
| − | [[Datei:P ID2361 KC T 1 5 S3 v2.png| | + | [[Datei:P ID2361 KC T 1 5 S3 v2.png|right|frame|Aufteilung der $2^k$ Fehlervektoren in „Cosets”|class=fit]] |
Man erkennt aus dieser Grafik: | Man erkennt aus dieser Grafik: | ||
| − | *Die $2^n = 32$ möglichen Fehlervektoren $\underline{e}$ werden in $2^m = 8$ „Cosets” ${\it \Psi}_0$, ... , ${\it \Psi}_7$ aufgeteilt. | + | *Die $2^n = 32$ möglichen Fehlervektoren $\underline{e}$ werden in $2^m = 8$ „Cosets” ${\it \Psi}_0$, ... , ${\it \Psi}_7$ aufgeteilt. |
| − | *Explizit gezeichnet sind hier nur die Cosets ${\it \Psi}_0$ und ${\it \Psi}_5$.<br> | + | *Explizit gezeichnet sind hier nur die Cosets ${\it \Psi}_0$ und ${\it \Psi}_5$.<br> |
| − | *Alle $2^k = 4$ Fehlervektoren des Cosets ${\it \Psi}_\mu$ führen zum | + | *Alle $2^k = 4$ Fehlervektoren des Cosets ${\it \Psi}_\mu$ führen zum Syndrom $\underline{s}_\mu$. |
| − | *Jede Nebenklasse ${\it \Psi}_\mu$ hat einen Anführer $\underline{e}_\mu$, nämlich denjenigen mit dem minimalen Hamming–Gewicht.}}<br> | + | *Jede Nebenklasse ${\it \Psi}_\mu$ hat einen Anführer $\underline{e}_\mu$, nämlich denjenigen mit dem minimalen Hamming–Gewicht.}}<br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 3:}$ Ausgehend vom systematischen $\text{(5, 2, 3)}$–Code $\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \big \}$ wird nun die Vorgehensweise bei der Syndromdecodierung im Detail beschrieben. | + | $\text{Beispiel 3:}$ Ausgehend vom systematischen $\text{(5, 2, 3)}$–Code $\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \big \}$ wird nun die Vorgehensweise bei der Syndromdecodierung im Detail beschrieben. |
| − | [[Datei:P ID2362 KC T 1 5 S3b v2.png|right|frame|Beispielhafte $\text{(5, 2, 3)}$–Syndromtabelle mit Nebenklassen|class=fit]] | + | [[Datei:P ID2362 KC T 1 5 S3b v2.png|right|frame|Beispielhafte $\text{(5, 2, 3)}$–Syndromtabelle mit Nebenklassen|class=fit]] |
| − | Generatormatrix und Prüfmatrix lauten: | + | Die Generatormatrix und die Prüfmatrix lauten: |
::<math>{ \boldsymbol{\rm G} } | ::<math>{ \boldsymbol{\rm G} } | ||
| Zeile 155: | Zeile 155: | ||
Die Tabelle fasst das Endergebnis zusammen. Beachten Sie: | Die Tabelle fasst das Endergebnis zusammen. Beachten Sie: | ||
| − | *Der Index $\mu$ ist nicht identisch mit dem Binärwert von $\underline{s}_\mu$. | + | *Der Index $\mu$ ist nicht identisch mit dem Binärwert von $\underline{s}_\mu$. |
| − | *Die Reihenfolge ergibt sich vielmehr durch die Anzahl der Einsen im Nebenklassenanführer $\underline{e}_\mu$. | + | *Die Reihenfolge ergibt sich vielmehr durch die Anzahl der Einsen im Nebenklassenanführer $\underline{e}_\mu$. |
| − | *Beispielsweise ist das Syndrom $\underline{s}_5 = (1, 1, 0)$ und das Syndrom $\underline{s}_6 = (1, 0, 1)$.<br> | + | *Beispielsweise ist das Syndrom $\underline{s}_5 = (1, 1, 0)$ und das Syndrom $\underline{s}_6 = (1, 0, 1)$.<br> |
Zur Herleitung dieser Tabelle ist anzumerken: | Zur Herleitung dieser Tabelle ist anzumerken: | ||
| − | *Die Zeile 1 bezieht sich auf das Syndrom $\underline{s}_0 = (0, 0, 0)$ und die dazugehörige Nebenklasse ${\it \Psi}_0$. Am wahrscheinlichsten ist hier die Fehlerfolge $(0, 0, 0, 0, 0)$ ⇒ kein Bitfehler, die wir als Nebenklassenanführer $\underline{e}_0$ bezeichnen. | + | *Die Zeile 1 bezieht sich auf das Syndrom $\underline{s}_0 = (0, 0, 0)$ und die dazugehörige Nebenklasse ${\it \Psi}_0$. Am wahrscheinlichsten ist hier die Fehlerfolge $(0, 0, 0, 0, 0)$ ⇒ kein Bitfehler, die wir als Nebenklassenanführer $\underline{e}_0$ bezeichnen. |
| − | *Auch die weiteren Einträge in der ersten Zeile, nämlich $(1, 0, 1, 1, 0 )$, $(0, 1, 0, 1, 1)$ und $(1, 1, 1, 0, 1 )$, liefern jeweils das Syndrom $\underline{s}_0 = (0, 0, 0)$, ergeben sich aber nur mit mindestens drei Bitfehlern und sind entsprechend unwahrscheinlich.<br> | + | *Auch die weiteren Einträge in der ersten Zeile, nämlich $(1, 0, 1, 1, 0 )$, $(0, 1, 0, 1, 1)$ und $(1, 1, 1, 0, 1 )$, liefern jeweils das Syndrom $\underline{s}_0 = (0, 0, 0)$, ergeben sich aber nur mit mindestens drei Bitfehlern und sind entsprechend unwahrscheinlich.<br> |
| − | *In den Zeilen 2 bis 6 beinhaltet der jeweilige Nebenklassenanführer $\underline{e}_\mu$ genau eine einzige Eins ( | + | *In den Zeilen 2 bis 6 beinhaltet der jeweilige Nebenklassenanführer $\underline{e}_\mu$ genau eine einzige Eins $(\mu = 1$, ... , $5)$. Dabei ist $\underline{e}_\mu$ stets das wahrscheinlichste Fehlermuster der Klasse ${\it \Psi}_\mu$. Die anderen Gruppenmitglieder ergeben sich erst bei mindestens zwei Bitfehlern.<br> |
| − | *Das Syndrom $\underline{s}_6 = (1, 0, 1)$ ist mit nur einem Bitfehler nicht möglich. Bei der Erstellung der Tabelle wurden daraufhin alle $5\text{ über }2 = 10$ Fehlermuster $\underline{e}$ mit Gewicht $w_{\rm H}(\underline{e}) = 2$ betrachtet. | + | *Das Syndrom $\underline{s}_6 = (1, 0, 1)$ ist mit nur einem Bitfehler nicht möglich. Bei der Erstellung der Tabelle wurden daraufhin alle $5\text{ über }2 = 10$ Fehlermuster $\underline{e}$ mit Gewicht $w_{\rm H}(\underline{e}) = 2$ betrachtet. |
| − | *Die zuerst gefundene Folge mit Syndrom $\underline{s}_6 = (1, 0, 1)$ wurde als Nebenklassenanführer $\underline{e}_6 = (1, 1, 0, 0, 0)$ ausgewählt. Bei anderer Probierreihenfolge hätte sich auch die Folge $(0, 0, 1, 0, 1)$ aus ${\it \Psi}_6$ ergeben können.<br> | + | *Die zuerst gefundene Folge mit dem Syndrom $\underline{s}_6 = (1, 0, 1)$ wurde als Nebenklassenanführer $\underline{e}_6 = (1, 1, 0, 0, 0)$ ausgewählt. Bei anderer Probierreihenfolge hätte sich auch die Folge $(0, 0, 1, 0, 1)$ aus ${\it \Psi}_6$ ergeben können.<br> |
| − | *Ähnlich wurde bei der Bestimmung des Anführers $\underline{e}_7 = (0, 1, 1, 0, 0)$ der Nebenklasse ${\it \Psi}_7$ vorgegangen, die durch das einheitliche Syndrom $\underline{s}_7 = (1, 1, 1)$ gekennzeichnet ist. Auch in der Klasse ${\it \Psi}_7$ gibt es eine weitere Folge mit Hamming–Gewicht $w_{\rm H}(\underline{e}) = 2$, nämlich $(1, 0, 0, 0, 1)$.<br><br> | + | *Ähnlich wurde bei der Bestimmung des Anführers $\underline{e}_7 = (0, 1, 1, 0, 0)$ der Nebenklasse ${\it \Psi}_7$ vorgegangen, die durch das einheitliche Syndrom $\underline{s}_7 = (1, 1, 1)$ gekennzeichnet ist. Auch in der Klasse ${\it \Psi}_7$ gibt es eine weitere Folge mit Hamming–Gewicht $w_{\rm H}(\underline{e}) = 2$, nämlich $(1, 0, 0, 0, 1)$.<br><br> |
Die obige Tabelle muss nur einmal erstellt und kann beliebig oft genutzt werden. Zunächst muss das Syndrom ermittelt werden. Dieses | Die obige Tabelle muss nur einmal erstellt und kann beliebig oft genutzt werden. Zunächst muss das Syndrom ermittelt werden. Dieses | ||
| − | lautet beispielsweise für den Empfangsvektor $\underline{y} = (0, 1, 0, 0, 1)$: | + | lautet beispielsweise für den Empfangsvektor $\underline{y} = (0, 1, 0, 0, 1)$: |
::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T} = \begin{pmatrix} | ::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T} = \begin{pmatrix} | ||
0 &1 &0 &0 &1 | 0 &1 &0 &0 &1 | ||
| Zeile 187: | Zeile 187: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Mit dem Nebenklassenanführer $\underline{e}_2 = (0, 0, 0, 1, 0)$ aus obiger Tabelle (roter Eintrag für | + | Mit dem Nebenklassenanführer $\underline{e}_2 = (0, 0, 0, 1, 0)$ aus obiger Tabelle $($roter Eintrag für $\mu =2)$ gelangt man schließlich zum Decodierergebnis: |
::<math>\underline{z} = \underline{y} + \underline{e}_2 = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1) + (0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0) = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1) | ::<math>\underline{z} = \underline{y} + \underline{e}_2 = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1) + (0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0) = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1) | ||
| Zeile 194: | Zeile 194: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Fazit:}$ Aus | + | $\text{Fazit:}$ Aus diesen Beispielen geht schon hervor, dass die '''Syndromdecodierung mit einem erheblichen Aufwand''' verbunden ist, wenn man nicht wie bei zyklischen Codes gewisse Eigenschaften nutzen kann: |
| − | *Bei großen Blockcodelängen versagt diese Methode vollständig. So müsste man zur Decodierung eines [https://de.wikipedia.org/wiki/BCH-Code BCH–Codes] – die Abkürzung steht für deren Erfinder | + | *Bei großen Blockcodelängen versagt diese Methode vollständig. So müsste man zur Decodierung eines [https://de.wikipedia.org/wiki/BCH-Code BCH–Codes] – die Abkürzung steht für deren Erfinder '''B'''ose, '''C'''haudhuri und '''H'''ocquenghem – mit den Codeparametern $n = 511$, $k = 259$ und $d_{\rm min} = 61$ genau $2^{511-259} \approx 10^{76}$ Fehlermuster der Länge $511$ auswerten und abspeichern. |
| − | *Für diese | + | *Für diese und auch für andere Codes großer Blocklänge gibt es aber erfreulicherweise spezielle Decodieralgorithmen, die mit weniger Aufwand zum Erfolg führen.}} |
== Codiergewinn – Bitfehlerrate bei AWGN == | == Codiergewinn – Bitfehlerrate bei AWGN == | ||
<br> | <br> | ||
| − | Wir betrachten nun die [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung#Definition_der_Bitfehlerquote| Bitfehlerquote]] (oder Bitfehlerrate, englisch: <i>Bit Error Rate</i> , BER) für folgende Konstellation: | + | Wir betrachten nun die [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung#Definition_der_Bitfehlerquote| Bitfehlerquote]] (oder Bitfehlerrate, englisch: <i>Bit Error Rate</i> , BER) für folgende Konstellation: |
| − | [[Datei:P ID2364 KC T 1 5 S4 v2.png|right|frame|Bitfehlerrate bei $\text{(7, 4, 3)}$–Hamming–Codierung|class=fit]] | + | [[Datei:P ID2364 KC T 1 5 S4 v2.png|right|frame|Bitfehlerrate bei $\text{(7, 4, 3)}$–Hamming–Codierung|class=fit]] |
| − | *Hamming–Code $\text{HC (7, 4, 3)}$,<br> | + | *Hamming–Code $\text{HC (7, 4, 3)}$,<br> |
| + | *AWGN–Kanal, gekennzeichnet durch den Quotienten $E_{\rm B}/N_0$ (in dB),<br> | ||
| − | * | + | *Maximum–Likelihood–Detektion (ML) mit <i>Hard Decision</i> bzw. <i>Soft Decision</i>. |
| − | |||
| − | |||
Zu dieser Grafik ist anzumerken: | Zu dieser Grafik ist anzumerken: | ||
| − | *Die schwarze Vergleichskurve gilt beispielsweise für die binäre Phasenmodulation (BPSK) ohne Codierung. Hierfür benötigt man für die Bitfehlerrate $10^{-5}$ etwa $10 \cdot \lg \, E_{\rm B}/N_0 = 9.6 \, \rm dB$.<br> | + | *Die schwarze Vergleichskurve gilt beispielsweise für die binäre Phasenmodulation (BPSK) ohne Codierung. Hierfür benötigt man für die Bitfehlerrate $10^{-5}$ etwa $10 \cdot \lg \, E_{\rm B}/N_0 = 9.6 \, \rm dB$.<br> |
| − | *Die roten Kreise gelten für den [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Einige_Eigenschaften_des_.287.2C_4.2C_3.29.E2.80.93Hamming.E2.80.93Codes|$\text{(7, 4, 3)}$–Code]] und harte Entscheidungen des Maximum–Likelihood–Decoders $\text{(ML–HD)}$. Die Syndromdecodierung ist hierfür eine mögliche Realisierungsform.<br> | + | *Die roten Kreise gelten für den [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Einige_Eigenschaften_des_.287.2C_4.2C_3.29.E2.80.93Hamming.E2.80.93Codes|$\text{(7, 4, 3)}$–Code]] und harte Entscheidungen des Maximum–Likelihood–Decoders $\text{(ML–HD)}$. Die Syndromdecodierung ist hierfür eine mögliche Realisierungsform.<br> |
| − | *Diese | + | *Diese Konfiguration bringt erst für $10 \cdot \lg \, E_{\rm B}/N_0 >6 \, \rm dB$ eine Verbesserung gegenüber dem Vergleichssystem. Für $\rm BER =10^{-5}$ benötigt man nur noch $10 \cdot \lg \, E_{\rm B}/N_0 \approx 9.2 \, \rm dB$.<br> |
| − | *Die grünen Kreuze für den Hamming–Code | + | *Die grünen Kreuze für den Hamming–Code und [[Kanalcodierung/Klassifizierung_von_Signalen#ML.E2.80.93Entscheidung_beim_AWGN.E2.80.93Kanal| Soft–Decision]] $\text{(ML–SD)}$ liegen im gesamten Bereich unterhalb der Vergleichskurve. Für $\rm BER =10^{-5}$ ergibt sich $10 \cdot \lg \, E_{\rm B}/N_0 \approx 7.8 \, \rm dB$.<br><br> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Als '''Codiergewinn''' einer Systemkonfiguration (gekennzeichnet durch seinen Code und die Art der Decodierung) bezeichnen wir das gegenüber dem Vergleichssystem (ohne Codierung) kleinere $10 \cdot \lg \, E_{\rm B}/N_0$, das für eine vorgegebene Bitfehlerrate $\rm (BER)$ erforderlich ist: | + | $\text{Definition:}$ Als '''Codiergewinn''' einer Systemkonfiguration (gekennzeichnet durch seinen Code und die Art der Decodierung) bezeichnen wir das gegenüber dem Vergleichssystem (ohne Codierung) kleinere $10 \cdot \lg \, E_{\rm B}/N_0$, das für eine vorgegebene Bitfehlerrate $\rm (BER)$ erforderlich ist: |
::<math>G_{\rm Code} (\hspace{0.05cm}{\rm System}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm}) =10 \cdot {\rm lg}\hspace{0.1cm}{E}_{\rm B}/N_0 | ::<math>G_{\rm Code} (\hspace{0.05cm}{\rm System}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm}) =10 \cdot {\rm lg}\hspace{0.1cm}{E}_{\rm B}/N_0 | ||
| Zeile 228: | Zeile 227: | ||
\hspace{0.05cm}. </math>}}<br> | \hspace{0.05cm}. </math>}}<br> | ||
| − | Angewendet auf obige Grafik erhält man: | + | Angewendet auf die obige Grafik erhält man: |
:<math>G_{\rm Code} (\hspace{0.05cm}{\rm Hamming \hspace{0.1cm}(7,\hspace{0.02cm}4,\hspace{0.02cm}3), ML-HD}\hspace{0.05cm}|\hspace{0.05cm}{\rm BER} = 10^{-5}\hspace{0.05cm}) = 0.4\ {\rm dB}\hspace{0.05cm},</math> | :<math>G_{\rm Code} (\hspace{0.05cm}{\rm Hamming \hspace{0.1cm}(7,\hspace{0.02cm}4,\hspace{0.02cm}3), ML-HD}\hspace{0.05cm}|\hspace{0.05cm}{\rm BER} = 10^{-5}\hspace{0.05cm}) = 0.4\ {\rm dB}\hspace{0.05cm},</math> | ||
| Zeile 236: | Zeile 235: | ||
== Decodierung beim Binary Erasure Channel == | == Decodierung beim Binary Erasure Channel == | ||
<br> | <br> | ||
| − | Abschließend soll noch gezeigt werden, in wie weit der Decoder zu modifizieren ist, wenn anstelle des [[Kanalcodierung/Klassifizierung_von_Signalen#Binary_Symmetric_Channel_.E2.80.93_BSC| BSC–Modells]] (<i>Binary Symmetric Channel</i> ) das [[Kanalcodierung/Klassifizierung_von_Signalen#Binary_Erasure_Channel_.E2.80.93_BEC| BEC–Kanalmodell]] (<i>Binary Erasure Channel</i> ) zum Einsatz kommt, der keine Fehler produziert, sondern unsichere Bit als Auslöschungen markiert.<br> | + | Abschließend soll noch gezeigt werden, in wie weit der Decoder zu modifizieren ist, wenn anstelle des [[Kanalcodierung/Klassifizierung_von_Signalen#Binary_Symmetric_Channel_.E2.80.93_BSC| BSC–Modells]] (<i>Binary Symmetric Channel</i> ) das [[Kanalcodierung/Klassifizierung_von_Signalen#Binary_Erasure_Channel_.E2.80.93_BEC| BEC–Kanalmodell]] (<i>Binary Erasure Channel</i> ) zum Einsatz kommt, der keine Fehler produziert, sondern unsichere Bit als Auslöschungen markiert.<br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 4:}$ Ohne Einschränkung der Allgemeingültigkeit betrachten wir wie im [[Kanalcodierung/Decodierung_linearer_Blockcodes#Verallgemeinerung_der_Syndromdecodierung|Beispiel 3]] wieder den systematischen $\text{(5, 2, 3)}$–Blockcode $\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \big \}$ | + | $\text{Beispiel 4:}$ Ohne Einschränkung der Allgemeingültigkeit betrachten wir wie im [[Kanalcodierung/Decodierung_linearer_Blockcodes#Verallgemeinerung_der_Syndromdecodierung|$\text{Beispiel 3}$]] wieder den systematischen $\text{(5, 2, 3)}$–Blockcode |
| + | :$$\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \big \}.$$ | ||
| − | [[Datei: | + | [[Datei:KC_T_1_5_S5nev.png|right|frame|Zur Fehlerkorrektur bei BSC und BEC]] |
| − | + | Die Grafik zeigt das Systemmodell und gibt beispielhafte Werte für die einzelnen Vektoren wider. | |
| − | *Der linke Bildteil ( | + | *Der linke Bildteil (gelb hinterlegt) gilt für „BSC” mit einem Bitfehler $0 → 1$ beim dritten Bit. |
| − | *Der rechte Bildteil (grün hinterlegt) gilt für | + | *Der rechte Bildteil (grün hinterlegt) gilt für „BEC” und zeigt zwei <i>Erasures</i> $\rm 1 → E$ bei Bit 2 und Bit 4. |
Man erkennt: | Man erkennt: | ||
| − | *Bei BSC kann wegen $d_{\rm min} = 3$ nur ein Bitfehler korrigiert werden ($t = 1$, rot markiert). Beschränkt man sich auf Fehlererkennung, so funktioniert diese bis zu $e= d_{\rm min} -1 = 2$ Bitfehler.<br> | + | *Bei BSC kann wegen $d_{\rm min} = 3$ nur ein Bitfehler korrigiert werden ($t = 1$, rot markiert). Beschränkt man sich auf Fehlererkennung, so funktioniert diese bis zu $e= d_{\rm min} -1 = 2$ Bitfehler.<br> |
| − | *Bei BEC macht Fehlererkennung keinen Sinn, denn bereits der Kanal lokalisiert ein unsicheres Bit als <i>Erasure</i> $\rm E$ (Auslöschung). Die Nullen und Einsen im BEC–Empfangswort $\underline{y}$ sind sicher. Deshalb funktioniert hier die Fehlerkorrektur bis zu $e = 2$ Auslöschungen mit Sicherheit.<br> | + | *Bei BEC macht Fehlererkennung keinen Sinn, denn bereits der Kanal lokalisiert ein unsicheres Bit als <i>Erasure</i> $\rm E$ (Auslöschung). Die Nullen und Einsen im BEC–Empfangswort $\underline{y}$ sind sicher. Deshalb funktioniert hier die Fehlerkorrektur bis zu $e = 2$ Auslöschungen mit Sicherheit.<br> |
| − | *Auch $e = 3$ Auslöschungen sind manchmal noch korrigierbar. So kann $\underline{y} \rm = (E, E, E, 1, 1)$ zu $\underline{z} \rm = (0, 1, 0, 1, 1)$ korrigiert werden, da kein zweites Codewort mit zwei Einsen endet. $\underline{y} \rm = (0, E, 0, E, E)$ ist aber aufgrund des im Code erlaubten Nullwortes nicht korrigierbar.<br> | + | *Auch $e = 3$ Auslöschungen sind manchmal noch korrigierbar. So kann $\underline{y} \rm = (E, E, E, 1, 1)$ zu $\underline{z} \rm = (0, 1, 0, 1, 1)$ korrigiert werden, da kein zweites Codewort mit zwei Einsen endet. $\underline{y} \rm = (0, E, 0, E, E)$ ist aber aufgrund des im Code erlaubten Nullwortes nicht korrigierbar.<br> |
| − | *Wird sichergestellt, dass in keinem Empfangswort mehr als zwei Auslöschungen vorkommen, so ist die BEC–Blockfehlerwahrscheinlichkeit ${\rm Pr}(\underline{z} \ne \underline{x}) = {\rm Pr}(\underline{v} \ne \underline{u}) \equiv 0$. Dagegen hat die entsprechende Blockfehlerwahrscheinlichkeit beim BSC–Modell stets einen Wert größer als $0$. | + | *Wird sichergestellt, dass in keinem Empfangswort mehr als zwei Auslöschungen vorkommen, so ist die BEC–Blockfehlerwahrscheinlichkeit ${\rm Pr}(\underline{z} \ne \underline{x}) = {\rm Pr}(\underline{v} \ne \underline{u}) \equiv 0$. Dagegen hat die entsprechende Blockfehlerwahrscheinlichkeit beim BSC–Modell stets einen Wert größer als $0$. |
| − | |||
| − | Wie funktioniert aber nun die Decodierung eines Empfangswortes $\underline{y}$ mit Auslöschungen algorithmisch? | + | Da nach dem BEC ein jedes Empfangswort entweder richtig oder gar nicht decodiert wird, nennen wir hier den Block $\underline{y} → \underline{z}$ zukünftig „Codewortfinder”. Eine „Schätzung” findet nur beim BSC–Modell statt.<br>}}<br> |
| + | |||
| + | Wie funktioniert aber nun die Decodierung eines Empfangswortes $\underline{y}$ mit Auslöschungen algorithmisch? | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 5:}$ Ausgehend vom Empfangswort $\underline{y} \rm = (0, E, 0, E, 1)$ im $\text{Beispiel 4}$ setzen wir den Ausgang des Codewortfinders formal zu $\underline{z} \rm = (0, z_2, 0, z_4, 1)$, wobei die Symbole $z_2 \in \{0, \, 1\}$ und $z_4 \in \{0, \, 1\}$ entsprechend folgender Gleichung zu bestimmen sind: | + | $\text{Beispiel 5:}$ Ausgehend vom Empfangswort $\underline{y} \rm = (0, E, 0, E, 1)$ im $\text{Beispiel 4}$ setzen wir den Ausgang des Codewortfinders formal zu $\underline{z} \rm = (0, z_2, 0, z_4, 1)$, wobei die Symbole $z_2 \in \{0, \, 1\}$ und $z_4 \in \{0, \, 1\}$ entsprechend folgender Gleichung zu bestimmen sind: |
::<math>\underline{z} \cdot { \boldsymbol{\rm H} }^{\rm T}= \underline{0} | ::<math>\underline{z} \cdot { \boldsymbol{\rm H} }^{\rm T}= \underline{0} | ||
| Zeile 268: | Zeile 269: | ||
Es geht nun darum, diese Bestimmungsgleichung möglichst effizient umzusetzen. Es ergeben sich folgende Rechenschritte: | Es geht nun darum, diese Bestimmungsgleichung möglichst effizient umzusetzen. Es ergeben sich folgende Rechenschritte: | ||
| − | *Mit der Prüfmatrix $\boldsymbol{\rm H}$ des $\text{(5, 2, 3)}$–Blockcodes und dem Vektor $\underline{z} \rm = (0, z_2, 0, z_4, 1)$ lautet die obige Bestimmungsgleichung: | + | *Mit der Prüfmatrix $\boldsymbol{\rm H}$ des $\text{(5, 2, 3)}$–Blockcodes und dem Vektor $\underline{z} \rm = (0, z_2, 0, z_4, 1)$ lautet die obige Bestimmungsgleichung: |
::<math>{ \boldsymbol{\rm H} } \cdot \underline{z}^{\rm T} | ::<math>{ \boldsymbol{\rm H} } \cdot \underline{z}^{\rm T} | ||
| Zeile 288: | Zeile 289: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Wir fassen die sicheren (korrekten) Bit zum Vektor $\underline{z}_{\rm K}$ zusammen und die ausgelöschten Bit zum Vektor $\underline{z}_{\rm E}$. Dann teilen wir die Prüfmatrix $\boldsymbol{\rm H}$ in die entsprechenden Teilmatrizen $\boldsymbol{\rm H}_{\rm K}$ und $\boldsymbol{\rm H}_{\rm E}$ auf: | + | *Wir fassen die sicheren (korrekten) Bit zum Vektor $\underline{z}_{\rm K}$ zusammen und die ausgelöschten Bit zum Vektor $\underline{z}_{\rm E}$. Dann teilen wir die Prüfmatrix $\boldsymbol{\rm H}$ in die entsprechenden Teilmatrizen $\boldsymbol{\rm H}_{\rm K}$ und $\boldsymbol{\rm H}_{\rm E}$ auf: |
::<math>\underline{z}_{\rm K} =(0, 0, 1)\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm H} }_{\rm K}= | ::<math>\underline{z}_{\rm K} =(0, 0, 1)\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm H} }_{\rm K}= | ||
| Zeile 309: | Zeile 310: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Unter Berücksichtigung der Tatsache, dass in $\rm GF(2)$ die Subtraktion gleich der Addition ist, lässt sich die obige Gleichung wie folgt darstellen: | + | *Unter Berücksichtigung der Tatsache, dass in $\rm GF(2)$ die Subtraktion gleich der Addition ist, lässt sich die obige Gleichung wie folgt darstellen: |
::<math>{ \boldsymbol{\rm H} }_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} | ::<math>{ \boldsymbol{\rm H} }_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} | ||
| Zeile 343: | Zeile 344: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Dies führt zu einem linearen Gleichungssystem mit zwei Gleichungen für die unbekannten $z_2$ und $z_4$ (jeweils $0$ oder $1$ | + | *Dies führt zu einem linearen Gleichungssystem mit zwei Gleichungen für die unbekannten $z_2$ und $z_4$ $($jeweils $0$ oder $1)$. |
| − | *Aus der letzten Zeile folgt $z_2 = 1$ und aus der zweiten Zeile $z_2 + z_4 = 0$ ⇒ $z_4 = 1$. | + | *Aus der letzten Zeile folgt $z_2 = 1$ und aus der zweiten Zeile $z_2 + z_4 = 0$ ⇒ $z_4 = 1$. |
| − | *Damit ergibt sich das zulässige Codewort $\underline{z} \rm = (0, 1, 0, 1, 1)$.}}<br> | + | *Damit ergibt sich das zulässige Codewort $\underline{z} \rm = (0, 1, 0, 1, 1)$.}}<br> |
== Aufgaben zum Kapitel == | == Aufgaben zum Kapitel == | ||
Aktuelle Version vom 20. Juli 2022, 14:38 Uhr
Inhaltsverzeichnis
Blockschaltbild und Voraussetzungen
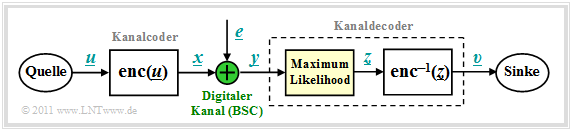
Wir gehen von dem bereits im Kapitel "Kanalmodelle und Entscheiderstrukturen" gezeigten Blockschaltbild aus, wobei als Kanalmodell meist der "Binary Symmetric Channel" $\rm (BSC)$ verwendet wird. Zur Codewortschätzung verwenden wir den "Maximum–Likelihood–Entscheider" $\rm (ML)$, der für binäre Codes ⇒ $\underline{x} \in {\rm GF}(2^n)$ auf Blockebene das gleiche Ergebnis liefert wie der "MAP–Empfänger".
Die Aufgabe des Kanaldecoders kann wie folgt beschrieben werden:
- Der Vektor $\underline{v}$ nach der Decodierung (an der Sinke) soll möglichst gut mit dem Informationswort $\underline{u}$ übereinstimmen.
Das heißt: Die Blockfehlerwahrscheinlichkeit soll möglichst klein sein:
- \[{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]
- Aufgrund der deterministischen Zuweisungen $\underline{x} = {\rm enc}(\underline{u})$ bzw. $\underline{v} = {\rm enc}^{-1}(\underline{z})$ gilt aber auch:
- \[{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{z} \ne \underline{x}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]
- Gesucht ist somit das zum gegebenen Empfangswort $\underline{y} = \underline{x} +\underline{e}$ am wahrscheinlichsten gesendete Codewort $\underline{x}_i$, das als Ergebnis $\underline{z}$ weiter gegeben wird:
- \[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.\]
- Beim BSC–Kanal gilt sowohl $\underline{x}_i \in {\rm GF}(2^n)$ als auch $\underline{y} \in {\rm GF}(2^n)$, so dass die Maximum–Likelihood–Regel auch mit der Hamming–Distanz $d_{\rm H}( \underline{y}, \, \underline{x}_i)$ geschrieben werden kann:
- \[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]
Prinzip der Syndromdecodierung
Vorausgesetzt wird hier ein $(n, \, k)$–Blockcode mit der Prüfmatrix $\boldsymbol{\rm H}$ und den systematischen Codeworten
- \[\underline{x}\hspace{0.05cm} = (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) = (u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k, p_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, p_{n-k})\hspace{0.05cm}. \]
Mit dem Fehlervektor $\underline{e}$ gilt dann für das Empfangswort:
- \[\underline{y} = \underline{x} + \underline{e} \hspace{0.05cm}, \hspace{0.4cm} \underline{y} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{x} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{e} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}.\]
Ein Bitfehler an der Position $i$, das heißt $y_i ≠ x_i$, wird ausgedrückt durch den Fehlerkoeffizienten $e_i = 1$.
$\text{Definition:}$ Das Syndrom $\underline{s} = (s_0, s_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, s_{m-1})$ berechnet sich (als Zeilen– bzw. Spaltenvektor) aus dem Empfangswort $\underline{y}$ und der Prüfmatrix $\boldsymbol{\rm H}$ wie folgt:
- \[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T}\hspace{0.3cm}{\rm bzw.}\hspace{0.3cm} \underline{s}^{\rm T} = { \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T}\hspace{0.05cm}.\]
Die Vektorlänge von $\underline{s}$ ist gleich $m = n-k$ $($Zeilenzahl von $\boldsymbol{\rm H})$.
Das Syndrom $\underline{s}$ zeigt folgende Charakteristika:
- Wegen der Gleichung $\underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{0}$ hängt das Syndrom $\underline{s}$ nicht vom Codewort $\underline{x}$ ab, sondern allein vom Fehlervektor $\underline{e}$:
- \[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} = \hspace{0.05cm} \underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} + \hspace{0.05cm} \underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} = \hspace{0.05cm} \underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} \hspace{0.05cm}.\]
- Bei hinreichend wenig Bitfehlern liefert $\underline{s}$ einen eindeutigen Hinweis auf die Fehlerpositionen und ermöglicht so eine vollständige Fehlerkorrektur.
$\text{Beispiel 1:}$ Ausgehend vom systematischen $\text{(7, 4, 3)}$–Hamming–Code erhält man für den Empfangsvektor $\underline{y} = (0, 1, 1, 1, 0, 0, 1)$ das folgende Ergebnis:
- \[{ \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} = \underline{s}^{\rm T} \hspace{0.05cm}.\]
Vergleicht man das Syndrom mit den Prüfgleichungen des Hamming–Codes, so erkennt man, dass
- am wahrscheinlichsten das vierte Symbol $(x_4 = u_4)$ des Codewortes verfälscht wurde,
- der Codewortschätzer somit das Ergebnis $\underline{z} = (0, 1, 1, 0, 0, 0, 1)$ liefern wird,
- die Entscheidung nur dann richtig ist, wenn bei der Übertragung nur ein Bit verfälscht wurde.
Nachfolgend sind die erforderlichen Korrekturen für den $\text{(7, 4, 3)}$–Hamming–Code angegeben, die sich aus dem errechneten Syndrom $\underline{s}$ entsprechend den Spalten der Prüfmatrix ergeben:
- \[\underline{s} = (0, 0, 0) \hspace{0.10cm} \Rightarrow\hspace{0.10cm}{\rm keine\hspace{0.15cm} Korrektur}\hspace{0.05cm};\hspace{0.8cm}\underline{s} = (1, 0, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm}p_1{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\]
- \[\underline{s} =(0, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} p_3{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{1.22cm}\underline{s} = (1, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_1{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\]
- \[\underline{s} =(0, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} p_2{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{1.22cm}\underline{s} = (1, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_3{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\]
- \[\underline{s} =(0, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_4{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{1.22cm}\underline{s} = (1, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_2{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm}. \]
Verallgemeinerung der Syndromdecodierung
Wir gehen weiterhin vom BSC–Kanalmodell aus. Das bedeutet:
- Der Empfangsvektor $\underline{y}$ und der Fehlervektor $\underline{e}$ sind Elemente von ${\rm GF}(2^n)$.
- Die möglichen Codeworte $\underline{x}_i$ gehören zum Code $\mathcal{C}$, der einen $(n-k)$–dimensionalen Untervektorraum von ${\rm GF}(2^n)$ aufspannt.
Unter dieser Voraussetzung fassen wir die Ergebnisse der letzten Seiten nochmals kurz zusammen:
- Die Syndromdecodierung ist eine Realisierungsmöglichkeit der Maximum–Likelihood–Detektion von Blockcodes. Man entscheidet sich für das Codewort $\underline{x}_i$ mit der geringsten Hamming–Distanz zum Empfangswort $\underline{y}$ :
- \[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]
- Die Syndromdecodierung ist aber auch die Suche nach dem wahrscheinlichsten Fehlervektor $\underline{e}$, der die Bedingung $\underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{s}$ erfüllt. Das Syndrom liegt dabei durch die Gleichung $\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} $ fest.
- Mit dem Hamming–Gewicht $w_{\rm H}(\underline{e})$ kann die zweite Interpretation auch wie folgt mathematisch formuliert werden:
- \[\underline{z} = \underline{y} + {\rm arg} \min_{\underline{e}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} {\rm GF}(2^n)} \hspace{0.1cm} w_{\rm H}(\underline{e}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]
$\text{Fazit:}$ Zu beachten ist, dass der Fehlervektor $\underline{e}$ ebenso wie der Empfangsvektor $\underline{y}$ ein Element von ${\rm GF}(2^n)$ ist im Gegensatz zum Syndrom $\underline{s} \in {\rm GF}(2^m)$ mit der Anzahl $m = n-k$ der Prüfgleichungen. Das bedeutet,
- dass die Zuordnung zwischen dem Syndrom $\underline{s}$ und dem Fehlervektor $\underline{e}$ nicht eindeutig ist, sondern
- dass jeweils $2^k$ Fehlervektoren zum gleichen Syndrom $\underline{s}$ führen, die man zu einer Nebenklasse (englisch: Coset ) zusammenfasst.
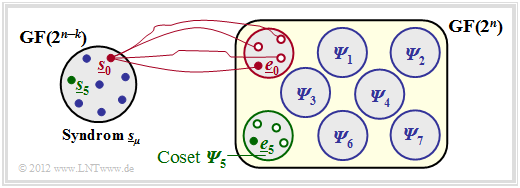
$\text{Beispiel 2:}$ Der Sachverhalt soll hier am Beispiel $n = 5, \ k = 2$ ⇒ $m = n-k = 3$ verdeutlicht werden.
Man erkennt aus dieser Grafik:
- Die $2^n = 32$ möglichen Fehlervektoren $\underline{e}$ werden in $2^m = 8$ „Cosets” ${\it \Psi}_0$, ... , ${\it \Psi}_7$ aufgeteilt.
- Explizit gezeichnet sind hier nur die Cosets ${\it \Psi}_0$ und ${\it \Psi}_5$.
- Alle $2^k = 4$ Fehlervektoren des Cosets ${\it \Psi}_\mu$ führen zum Syndrom $\underline{s}_\mu$.
- Jede Nebenklasse ${\it \Psi}_\mu$ hat einen Anführer $\underline{e}_\mu$, nämlich denjenigen mit dem minimalen Hamming–Gewicht.
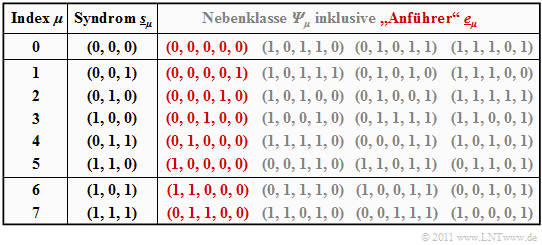
$\text{Beispiel 3:}$ Ausgehend vom systematischen $\text{(5, 2, 3)}$–Code $\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \big \}$ wird nun die Vorgehensweise bei der Syndromdecodierung im Detail beschrieben.
Die Generatormatrix und die Prüfmatrix lauten:
- \[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 &0 &1 &1 &0 \\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm},\]
- \[{ \boldsymbol{\rm H} } = \begin{pmatrix} 1 &0 &1 &0 &0 \\ 1 &1 &0 &1 &0 \\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.\]
Die Tabelle fasst das Endergebnis zusammen. Beachten Sie:
- Der Index $\mu$ ist nicht identisch mit dem Binärwert von $\underline{s}_\mu$.
- Die Reihenfolge ergibt sich vielmehr durch die Anzahl der Einsen im Nebenklassenanführer $\underline{e}_\mu$.
- Beispielsweise ist das Syndrom $\underline{s}_5 = (1, 1, 0)$ und das Syndrom $\underline{s}_6 = (1, 0, 1)$.
Zur Herleitung dieser Tabelle ist anzumerken:
- Die Zeile 1 bezieht sich auf das Syndrom $\underline{s}_0 = (0, 0, 0)$ und die dazugehörige Nebenklasse ${\it \Psi}_0$. Am wahrscheinlichsten ist hier die Fehlerfolge $(0, 0, 0, 0, 0)$ ⇒ kein Bitfehler, die wir als Nebenklassenanführer $\underline{e}_0$ bezeichnen.
- Auch die weiteren Einträge in der ersten Zeile, nämlich $(1, 0, 1, 1, 0 )$, $(0, 1, 0, 1, 1)$ und $(1, 1, 1, 0, 1 )$, liefern jeweils das Syndrom $\underline{s}_0 = (0, 0, 0)$, ergeben sich aber nur mit mindestens drei Bitfehlern und sind entsprechend unwahrscheinlich.
- In den Zeilen 2 bis 6 beinhaltet der jeweilige Nebenklassenanführer $\underline{e}_\mu$ genau eine einzige Eins $(\mu = 1$, ... , $5)$. Dabei ist $\underline{e}_\mu$ stets das wahrscheinlichste Fehlermuster der Klasse ${\it \Psi}_\mu$. Die anderen Gruppenmitglieder ergeben sich erst bei mindestens zwei Bitfehlern.
- Das Syndrom $\underline{s}_6 = (1, 0, 1)$ ist mit nur einem Bitfehler nicht möglich. Bei der Erstellung der Tabelle wurden daraufhin alle $5\text{ über }2 = 10$ Fehlermuster $\underline{e}$ mit Gewicht $w_{\rm H}(\underline{e}) = 2$ betrachtet.
- Die zuerst gefundene Folge mit dem Syndrom $\underline{s}_6 = (1, 0, 1)$ wurde als Nebenklassenanführer $\underline{e}_6 = (1, 1, 0, 0, 0)$ ausgewählt. Bei anderer Probierreihenfolge hätte sich auch die Folge $(0, 0, 1, 0, 1)$ aus ${\it \Psi}_6$ ergeben können.
- Ähnlich wurde bei der Bestimmung des Anführers $\underline{e}_7 = (0, 1, 1, 0, 0)$ der Nebenklasse ${\it \Psi}_7$ vorgegangen, die durch das einheitliche Syndrom $\underline{s}_7 = (1, 1, 1)$ gekennzeichnet ist. Auch in der Klasse ${\it \Psi}_7$ gibt es eine weitere Folge mit Hamming–Gewicht $w_{\rm H}(\underline{e}) = 2$, nämlich $(1, 0, 0, 0, 1)$.
Die obige Tabelle muss nur einmal erstellt und kann beliebig oft genutzt werden. Zunächst muss das Syndrom ermittelt werden. Dieses lautet beispielsweise für den Empfangsvektor $\underline{y} = (0, 1, 0, 0, 1)$:
- \[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T} = \begin{pmatrix} 0 &1 &0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 1 &1 &0 \\ 0 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \\ \end{pmatrix} = \begin{pmatrix} 0 &1 &0 \end{pmatrix}= \underline{s}_2 \hspace{0.05cm}.\]
Mit dem Nebenklassenanführer $\underline{e}_2 = (0, 0, 0, 1, 0)$ aus obiger Tabelle $($roter Eintrag für $\mu =2)$ gelangt man schließlich zum Decodierergebnis:
- \[\underline{z} = \underline{y} + \underline{e}_2 = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1) + (0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0) = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1) \hspace{0.05cm}.\]
$\text{Fazit:}$ Aus diesen Beispielen geht schon hervor, dass die Syndromdecodierung mit einem erheblichen Aufwand verbunden ist, wenn man nicht wie bei zyklischen Codes gewisse Eigenschaften nutzen kann:
- Bei großen Blockcodelängen versagt diese Methode vollständig. So müsste man zur Decodierung eines BCH–Codes – die Abkürzung steht für deren Erfinder Bose, Chaudhuri und Hocquenghem – mit den Codeparametern $n = 511$, $k = 259$ und $d_{\rm min} = 61$ genau $2^{511-259} \approx 10^{76}$ Fehlermuster der Länge $511$ auswerten und abspeichern.
- Für diese und auch für andere Codes großer Blocklänge gibt es aber erfreulicherweise spezielle Decodieralgorithmen, die mit weniger Aufwand zum Erfolg führen.
Codiergewinn – Bitfehlerrate bei AWGN
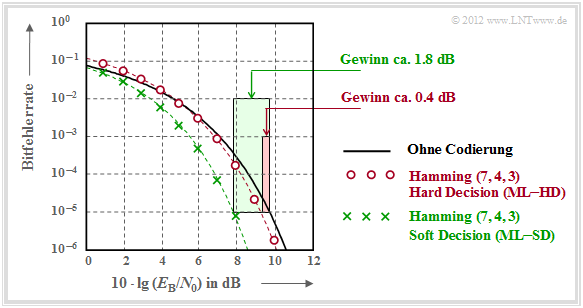
Wir betrachten nun die Bitfehlerquote (oder Bitfehlerrate, englisch: Bit Error Rate , BER) für folgende Konstellation:
- Hamming–Code $\text{HC (7, 4, 3)}$,
- AWGN–Kanal, gekennzeichnet durch den Quotienten $E_{\rm B}/N_0$ (in dB),
- Maximum–Likelihood–Detektion (ML) mit Hard Decision bzw. Soft Decision.
Zu dieser Grafik ist anzumerken:
- Die schwarze Vergleichskurve gilt beispielsweise für die binäre Phasenmodulation (BPSK) ohne Codierung. Hierfür benötigt man für die Bitfehlerrate $10^{-5}$ etwa $10 \cdot \lg \, E_{\rm B}/N_0 = 9.6 \, \rm dB$.
- Die roten Kreise gelten für den $\text{(7, 4, 3)}$–Code und harte Entscheidungen des Maximum–Likelihood–Decoders $\text{(ML–HD)}$. Die Syndromdecodierung ist hierfür eine mögliche Realisierungsform.
- Diese Konfiguration bringt erst für $10 \cdot \lg \, E_{\rm B}/N_0 >6 \, \rm dB$ eine Verbesserung gegenüber dem Vergleichssystem. Für $\rm BER =10^{-5}$ benötigt man nur noch $10 \cdot \lg \, E_{\rm B}/N_0 \approx 9.2 \, \rm dB$.
- Die grünen Kreuze für den Hamming–Code und Soft–Decision $\text{(ML–SD)}$ liegen im gesamten Bereich unterhalb der Vergleichskurve. Für $\rm BER =10^{-5}$ ergibt sich $10 \cdot \lg \, E_{\rm B}/N_0 \approx 7.8 \, \rm dB$.
$\text{Definition:}$ Als Codiergewinn einer Systemkonfiguration (gekennzeichnet durch seinen Code und die Art der Decodierung) bezeichnen wir das gegenüber dem Vergleichssystem (ohne Codierung) kleinere $10 \cdot \lg \, E_{\rm B}/N_0$, das für eine vorgegebene Bitfehlerrate $\rm (BER)$ erforderlich ist:
- \[G_{\rm Code} (\hspace{0.05cm}{\rm System}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm}) =10 \cdot {\rm lg}\hspace{0.1cm}{E}_{\rm B}/N_0 \hspace{0.15cm}(\hspace{0.05cm}{\rm ohne\hspace{0.1cm} Codierung}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm})- 10 \cdot {\rm lg}\hspace{0.1cm}{E}_{\rm B}/N_0 \hspace{0.15cm}(\hspace{0.05cm}{\rm System}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm}) \hspace{0.05cm}. \]
Angewendet auf die obige Grafik erhält man:
\[G_{\rm Code} (\hspace{0.05cm}{\rm Hamming \hspace{0.1cm}(7,\hspace{0.02cm}4,\hspace{0.02cm}3), ML-HD}\hspace{0.05cm}|\hspace{0.05cm}{\rm BER} = 10^{-5}\hspace{0.05cm}) = 0.4\ {\rm dB}\hspace{0.05cm},\]
\[G_{\rm Code} (\hspace{0.05cm}{\rm Hamming \hspace{0.1cm}(7,\hspace{0.02cm}4,\hspace{0.02cm}3), ML-SD}\hspace{0.05cm}|\hspace{0.05cm}{\rm BER} = 10^{-5}\hspace{0.05cm}) = 1.8\ {\rm dB}\hspace{0.05cm}.\]
Decodierung beim Binary Erasure Channel
Abschließend soll noch gezeigt werden, in wie weit der Decoder zu modifizieren ist, wenn anstelle des BSC–Modells (Binary Symmetric Channel ) das BEC–Kanalmodell (Binary Erasure Channel ) zum Einsatz kommt, der keine Fehler produziert, sondern unsichere Bit als Auslöschungen markiert.
$\text{Beispiel 4:}$ Ohne Einschränkung der Allgemeingültigkeit betrachten wir wie im $\text{Beispiel 3}$ wieder den systematischen $\text{(5, 2, 3)}$–Blockcode
- $$\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \big \}.$$
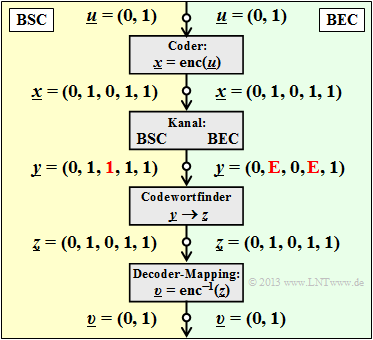
Die Grafik zeigt das Systemmodell und gibt beispielhafte Werte für die einzelnen Vektoren wider.
- Der linke Bildteil (gelb hinterlegt) gilt für „BSC” mit einem Bitfehler $0 → 1$ beim dritten Bit.
- Der rechte Bildteil (grün hinterlegt) gilt für „BEC” und zeigt zwei Erasures $\rm 1 → E$ bei Bit 2 und Bit 4.
Man erkennt:
- Bei BSC kann wegen $d_{\rm min} = 3$ nur ein Bitfehler korrigiert werden ($t = 1$, rot markiert). Beschränkt man sich auf Fehlererkennung, so funktioniert diese bis zu $e= d_{\rm min} -1 = 2$ Bitfehler.
- Bei BEC macht Fehlererkennung keinen Sinn, denn bereits der Kanal lokalisiert ein unsicheres Bit als Erasure $\rm E$ (Auslöschung). Die Nullen und Einsen im BEC–Empfangswort $\underline{y}$ sind sicher. Deshalb funktioniert hier die Fehlerkorrektur bis zu $e = 2$ Auslöschungen mit Sicherheit.
- Auch $e = 3$ Auslöschungen sind manchmal noch korrigierbar. So kann $\underline{y} \rm = (E, E, E, 1, 1)$ zu $\underline{z} \rm = (0, 1, 0, 1, 1)$ korrigiert werden, da kein zweites Codewort mit zwei Einsen endet. $\underline{y} \rm = (0, E, 0, E, E)$ ist aber aufgrund des im Code erlaubten Nullwortes nicht korrigierbar.
- Wird sichergestellt, dass in keinem Empfangswort mehr als zwei Auslöschungen vorkommen, so ist die BEC–Blockfehlerwahrscheinlichkeit ${\rm Pr}(\underline{z} \ne \underline{x}) = {\rm Pr}(\underline{v} \ne \underline{u}) \equiv 0$. Dagegen hat die entsprechende Blockfehlerwahrscheinlichkeit beim BSC–Modell stets einen Wert größer als $0$.
Da nach dem BEC ein jedes Empfangswort entweder richtig oder gar nicht decodiert wird, nennen wir hier den Block $\underline{y} → \underline{z}$ zukünftig „Codewortfinder”. Eine „Schätzung” findet nur beim BSC–Modell statt.
Wie funktioniert aber nun die Decodierung eines Empfangswortes $\underline{y}$ mit Auslöschungen algorithmisch?
$\text{Beispiel 5:}$ Ausgehend vom Empfangswort $\underline{y} \rm = (0, E, 0, E, 1)$ im $\text{Beispiel 4}$ setzen wir den Ausgang des Codewortfinders formal zu $\underline{z} \rm = (0, z_2, 0, z_4, 1)$, wobei die Symbole $z_2 \in \{0, \, 1\}$ und $z_4 \in \{0, \, 1\}$ entsprechend folgender Gleichung zu bestimmen sind:
- \[\underline{z} \cdot { \boldsymbol{\rm H} }^{\rm T}= \underline{0} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H} } \cdot \underline{z}^{\rm T}= \underline{0}^{\rm T} \hspace{0.05cm}.\]
Es geht nun darum, diese Bestimmungsgleichung möglichst effizient umzusetzen. Es ergeben sich folgende Rechenschritte:
- Mit der Prüfmatrix $\boldsymbol{\rm H}$ des $\text{(5, 2, 3)}$–Blockcodes und dem Vektor $\underline{z} \rm = (0, z_2, 0, z_4, 1)$ lautet die obige Bestimmungsgleichung:
- \[{ \boldsymbol{\rm H} } \cdot \underline{z}^{\rm T} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ z_2 \\ 0 \\ z_4 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \hspace{0.05cm}.\]
- Wir fassen die sicheren (korrekten) Bit zum Vektor $\underline{z}_{\rm K}$ zusammen und die ausgelöschten Bit zum Vektor $\underline{z}_{\rm E}$. Dann teilen wir die Prüfmatrix $\boldsymbol{\rm H}$ in die entsprechenden Teilmatrizen $\boldsymbol{\rm H}_{\rm K}$ und $\boldsymbol{\rm H}_{\rm E}$ auf:
- \[\underline{z}_{\rm K} =(0, 0, 1)\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm H} }_{\rm K}= \begin{pmatrix} 1 &1 &0\\ 1 &0 &0\\ 0 &0 &1 \end{pmatrix} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {\rm Spalten\hspace{0.15cm} 1,\hspace{0.15cm}3 \hspace{0.15cm}und \hspace{0.15cm}5 \hspace{0.15cm}der \hspace{0.15cm}Pr\ddot{u}fmatrix} \hspace{0.05cm},\]
- \[\underline{z}_{\rm E} = (z_2, z_4)\hspace{0.05cm},\hspace{0.35cm} { \boldsymbol{\rm H} }_{\rm E}= \begin{pmatrix} 0 &0\\ 1 &1\\ 1 &0 \end{pmatrix} \hspace{0.9cm}\Rightarrow\hspace{0.3cm} {\rm Spalten\hspace{0.15cm} 2 \hspace{0.15cm}und \hspace{0.15cm}4 \hspace{0.15cm}der \hspace{0.15cm}Pr\ddot{u}fmatrix} \hspace{0.05cm}.\]
- Unter Berücksichtigung der Tatsache, dass in $\rm GF(2)$ die Subtraktion gleich der Addition ist, lässt sich die obige Gleichung wie folgt darstellen:
- \[{ \boldsymbol{\rm H} }_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} + { \boldsymbol{\rm H} }_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= \underline{0}^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H} }_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H} }_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \begin{pmatrix} 0 &0\\ 1 &1\\ 1 &0 \end{pmatrix} \cdot \begin{pmatrix} z_2 \\ z_4 \end{pmatrix} = \begin{pmatrix} 1 &1 &0\\ 1 &0 &0\\ 0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \hspace{0.05cm}.\]
- Dies führt zu einem linearen Gleichungssystem mit zwei Gleichungen für die unbekannten $z_2$ und $z_4$ $($jeweils $0$ oder $1)$.
- Aus der letzten Zeile folgt $z_2 = 1$ und aus der zweiten Zeile $z_2 + z_4 = 0$ ⇒ $z_4 = 1$.
- Damit ergibt sich das zulässige Codewort $\underline{z} \rm = (0, 1, 0, 1, 1)$.
Aufgaben zum Kapitel
Aufgabe 1.11: Syndromdecodierung
Aufgabe 1.11Z: Nochmals Syndromdecodierung
Aufgabe 1.12: Hard Decision vs. Soft_Decision
Aufgabe 1.12Z: Vergleich von HC (7, 4, 3) und HC (8, 4, 4)
Aufgabe 1.13: Decodierung beim binären Auslöschungskanal (BEC)
Aufgabe 1.13Z: Nochmals BEC–Decodierung