Aufgaben:Aufgabe 3.4: Dämpfungs- und Phasenverlauf: Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1768__LZI_A_3_4.png|right|frame|Pol–Nullstellen–Diagramm | + | [[Datei:P_ID1768__LZI_A_3_4.png|right|frame|Pol–Nullstellen–Diagramm sowie Definition einiger Hilfsgrößen]] |
Wir gehen vom skizzierten Pol–Nullstellen–Diagramm aus, also von den Werten | Wir gehen vom skizzierten Pol–Nullstellen–Diagramm aus, also von den Werten | ||
:$$K = 5, \hspace{0,2cm}Z = 1, \hspace{0,2cm}N = 2, $$ | :$$K = 5, \hspace{0,2cm}Z = 1, \hspace{0,2cm}N = 2, $$ | ||
:$$ p_{\rm o}= 1,\hspace{0,2cm}p_{\rm x1}= -3 + 3{\rm j},\hspace{0,2cm}p_{\rm x2}= -3 - 3{\rm j}\hspace{0.05cm} .$$ | :$$ p_{\rm o}= 1,\hspace{0,2cm}p_{\rm x1}= -3 + 3{\rm j},\hspace{0,2cm}p_{\rm x2}= -3 - 3{\rm j}\hspace{0.05cm} .$$ | ||
| − | Damit lautet die $p$–Übertragungsfunktion: | + | Damit lautet die $p$–Übertragungsfunktion: |
:$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} | :$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} | ||
{(p - p_{\rm x 1})(p - p_{\rm x 2})} | {(p - p_{\rm x 1})(p - p_{\rm x 2})} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | Mit der Substitution $p = {\rm j} \cdot 2 \pi f$ lässt sich die herkömmliche Übertragungsfunktion angeben, die auch als Frequenzgang bezeichnet wird: | + | Mit der Substitution $p = {\rm j} \cdot 2 \pi f$ lässt sich die herkömmliche Übertragungsfunktion angeben, die auch als Frequenzgang bezeichnet wird: |
:$$H(f) = H_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it | :$$H(f) = H_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it | ||
f}} = {\rm e}^{-a(f)\hspace{0.05cm}}\cdot {\rm e}^{- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} | f}} = {\rm e}^{-a(f)\hspace{0.05cm}}\cdot {\rm e}^{- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} | ||
| Zeile 19: | Zeile 19: | ||
Aus dieser Gleichung erkennt man auch den Zusammenhang zwischen | Aus dieser Gleichung erkennt man auch den Zusammenhang zwischen | ||
| − | * der Übertragungsfunktion $H(f)$, | + | * der Übertragungsfunktion $H(f)$, |
| − | *der Dämpfungsfunktion $a(f)$ und | + | *der Dämpfungsfunktion $a(f)$ und |
| − | *der Phasenfunktion $b(f)$. | + | *der Phasenfunktion $b(f)$. |
| − | Für eine durch den Punkt $p = {\rm j} \cdot 2 \pi f$ indirekt vorgegebene Frequenz $f$ kann man die Dämpfungs– und Phasenwerte wie folgt ermitteln: | + | Für eine durch den Punkt $p = {\rm j} \cdot 2 \pi f$ indirekt vorgegebene Frequenz $f$ kann man die Dämpfungs– und Phasenwerte wie folgt ermitteln: |
:$$a(f)\hspace{0.15cm}{\rm in}\hspace{0.15cm}{\rm Np} \hspace{0.25cm} = \hspace{0.2cm} -{\rm ln} \hspace{0.1cm} K | :$$a(f)\hspace{0.15cm}{\rm in}\hspace{0.15cm}{\rm Np} \hspace{0.25cm} = \hspace{0.2cm} -{\rm ln} \hspace{0.1cm} K | ||
+ {\rm ln} \hspace{0.1cm} |R_{\rm x1}|+{\rm ln} \hspace{0.1cm} |R_{\rm x1}|- {\rm ln} \hspace{0.1cm} |R_{{\rm o} }|\hspace{0.05cm} | + {\rm ln} \hspace{0.1cm} |R_{\rm x1}|+{\rm ln} \hspace{0.1cm} |R_{\rm x1}|- {\rm ln} \hspace{0.1cm} |R_{{\rm o} }|\hspace{0.05cm} | ||
| Zeile 32: | Zeile 32: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | Die entsprechenden Beträge $|R_{\rm o}|$, $|R_{\rm x1}|$ und$|R_{\rm | + | Die entsprechenden Beträge $|R_{\rm o}|$, $|R_{\rm x1}|$ und $|R_{\rm x2}|$ können Sie ebenso wie die Winkel $\phi_{\rm o}$, $\phi_{\rm x1}$ und $\phi_{\rm x2}$ der Grafik entnehmen. |
| Zeile 39: | Zeile 39: | ||
| − | '' | + | ''Hinweis:'' |
| − | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion|Laplace–Transformation und p–Übertragungsfunktion]]. | + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion|Laplace–Transformation und p–Übertragungsfunktion]]. |
| − | + | ||
| Zeile 49: | Zeile 49: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie $H(f)$. Wie groß ist dessen Betrag bei sehr großen Frequenzen? | + | {Berechnen Sie $H(f)$. Wie groß ist dessen Betrag bei sehr großen Frequenzen? |
|type="{}"} | |type="{}"} | ||
$|H(f → ∞)| \ = \ $ { 0. } | $|H(f → ∞)| \ = \ $ { 0. } | ||
| − | {Berechnen Sie den Betragsfrequenzgang und den Dämpfungswert für $f → 0$. | + | {Berechnen Sie den Betragsfrequenzgang und den Dämpfungswert für $f → 0$. |
|type="{}"} | |type="{}"} | ||
$|H(f = 0)| \ = \ $ { 0.278 3% } | $|H(f = 0)| \ = \ $ { 0.278 3% } | ||
| Zeile 60: | Zeile 60: | ||
| − | {Berechnen Sie gemäß der beschriebenen Vorgehensweise den Dämpfungswert bei $f 4/(2 \pi)$ in Neper (Np) und Dezibel (dB). | + | {Berechnen Sie gemäß der beschriebenen Vorgehensweise den Dämpfungswert bei $f =4/(2 \pi)$ in Neper $\rm(Np)$ und Dezibel $\rm(dB)$. |
|type="{}"} | |type="{}"} | ||
$a(f = 2/ \pi)\ = \ $ { 0.155 3% } $\ \rm Np$ | $a(f = 2/ \pi)\ = \ $ { 0.155 3% } $\ \rm Np$ | ||
| Zeile 66: | Zeile 66: | ||
| − | {Berechnen Sie gemäß der beschriebenen Vorgehensweise den Phasenwert bei der Frequenz $f 4/(2 \pi)$. | + | {Berechnen Sie gemäß der beschriebenen Vorgehensweise den Phasenwert bei der Frequenz $f = 4/(2 \pi)$. |
|type="{}"} | |type="{}"} | ||
$b(f = 2/ \pi)\ = \ $ { -19.3--18.3 } $\ \rm Grad$ | $b(f = 2/ \pi)\ = \ $ { -19.3--18.3 } $\ \rm Grad$ | ||
| Zeile 76: | Zeile 76: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die | + | '''(1)''' Die $p$–Übertragungsfunktion lautet: |
:$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} | :$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} | ||
{(p - p_{\rm x 1})(p - p_{\rm x 2})} | {(p - p_{\rm x 1})(p - p_{\rm x 2})} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | Zur herkömmlichen Übertragungsfunktion (Frequenzgang) kommt man mit der Substitution $p = {\rm j} \cdot 2 \pi f$: | + | *Zur herkömmlichen Übertragungsfunktion (zum Frequenzgang) kommt man mit der Substitution $p = {\rm j} \cdot 2 \pi f$: |
| − | $$H(f)= K \cdot \frac {{\rm j \hspace{0.05cm}2\pi \it | + | :$$H(f)= K \cdot \frac {{\rm j \hspace{0.05cm}2\pi \it |
f} - p_{\rm o }} | f} - p_{\rm o }} | ||
{({\rm j \hspace{0.05cm}2\pi \it | {({\rm j \hspace{0.05cm}2\pi \it | ||
| Zeile 90: | Zeile 90: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | Im Grenzfall $f → \infty$ ergibt sich für den Betrag, die Dämpfung und die Phase: | + | *Im Grenzfall $f → \infty$ ergibt sich für den Betrag, die Dämpfung und die Phase: |
| − | $$\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} H(f)= \frac{K}{{\rm j \hspace{0.05cm}2\pi \it | + | :$$\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} H(f)= \frac{K}{{\rm j \hspace{0.05cm}2\pi \it |
| − | f}}\hspace{0. | + | f}}\hspace{0.5cm}\Rightarrow \hspace{0.5cm}\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} |H(f)|\hspace{0.15cm}\underline {= 0} \hspace{0.5cm} |
| − | \Rightarrow \hspace{0. | + | \Rightarrow \hspace{0.5cm}\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} a(f)= \infty,\hspace{0.1cm} |
\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} b(f)\underline {= | \lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} b(f)\underline {= | ||
{\pi}/{2}\hspace{0.1cm}(+90^\circ)} | {\pi}/{2}\hspace{0.1cm}(+90^\circ)} | ||
\hspace{0.01cm}.$$ | \hspace{0.01cm}.$$ | ||
| − | '''(2)''' Aus der allgemeinen Gleichung in Teilaufgabe (1) erhält man mit dem Grenzübergang $f → 0$: | + | |
| − | $$|H(f=0)|= -\frac {K \cdot p_{\rm o }} | + | |
| + | '''(2)''' Aus der allgemeinen Gleichung in Teilaufgabe '''(1)''' erhält man mit dem Grenzübergang $f → 0$: | ||
| + | [[Datei:P_ID1769__LZI_A_3_4_d_neu.png|right|frame|$|H(f)|$, , $a(f)$ und $b(f)$]] | ||
| + | :$$|H(f=0)|= -\frac {K \cdot p_{\rm o }} | ||
{p_{\rm x 1}\cdot p_{\rm x 2}} | {p_{\rm x 1}\cdot p_{\rm x 2}} | ||
= \frac {5 \cdot 1}{ | = \frac {5 \cdot 1}{ | ||
| Zeile 105: | Zeile 108: | ||
0.278} | 0.278} | ||
\hspace{0.05cm} ,$$ | \hspace{0.05cm} ,$$ | ||
| − | $$a(f=0)=- {\rm ln} \hspace{0.1cm}\hspace{0.15cm}\underline { |H(f=0)|= 1.281\,{\rm Np }} | + | :$$a(f=0)=- {\rm ln} \hspace{0.1cm}\hspace{0.15cm}\underline { |H(f=0)|= 1.281\,{\rm Np }} |
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | ||
Der Bildschirmabzug des Flash–Moduls „Kausale Systeme” fasst die Ergebnisse dieser Aufgabe zusammen: | Der Bildschirmabzug des Flash–Moduls „Kausale Systeme” fasst die Ergebnisse dieser Aufgabe zusammen: | ||
| − | :*Mittlere Achse (blau): Betrag $|H(f)|$, | + | :*Mittlere Achse (blau): Betrag $|H(f)|$ ⇒ hier beschriftet mit $|Y(f)|$, |
| − | :*Linke Achse (rot): Dämpfung $a(f)$, | + | :*Linke Achse (rot): Dämpfung $a(f)$, |
| − | :*Rechte Achse (grün): Phase $b(f)$. | + | :*Rechte Achse (grün): Phase $b(f)$. |
:*Schwarzer Punkt: Werte für $2\pi f = 4.$ | :*Schwarzer Punkt: Werte für $2\pi f = 4.$ | ||
| − | |||
| − | '''(3)''' Entsprechend der detaillierten Beschreibung im [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Grafische_Ermittlung_von_D.C3.A4mpfung_und_Phase|Theorieteil]] gilt für die Dämpfungsfunktion: | + | [[Datei:P_ID2843__LZI_A_3_4.png|right|frame|Pol–Nullstellen–Diagramm und einige Hilfsgrößen]] |
| − | + | '''(3)''' Entsprechend der detaillierten Beschreibung im [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Grafische_Ermittlung_von_D.C3.A4mpfung_und_Phase|Theorieteil]] gilt für die Dämpfungsfunktion: | |
| − | $$a(f)= -{\rm ln} \hspace{0.1cm} K | + | |
| + | :$$a(f)= -{\rm ln} \hspace{0.1cm} K | ||
+ {\rm ln} \hspace{0.1cm} |R_{\rm x1}|+{\rm ln} \hspace{0.1cm} |R_{\rm x2}|- {\rm ln} \hspace{0.1cm} |R_{{\rm o} }|\hspace{0.05cm} .$$ | + {\rm ln} \hspace{0.1cm} |R_{\rm x1}|+{\rm ln} \hspace{0.1cm} |R_{\rm x2}|- {\rm ln} \hspace{0.1cm} |R_{{\rm o} }|\hspace{0.05cm} .$$ | ||
| − | Zu berücksichtigen ist weiterhin die Zusatzeinheit „Neper” (Np). | + | *Zu berücksichtigen ist weiterhin die Zusatzeinheit „Neper” $\rm (Np)$. |
| − | Gesucht ist die Dämpfung bei $f = 2/\pi$. Dazu setzen wir $p = {\rm j} \cdot 2 \pi f = 4$ und ermitteln folgende Abstände: | + | *Gesucht ist die Dämpfung bei $f = 2/\pi$. Dazu setzen wir $p = {\rm j} \cdot 2 \pi f = 4$ und ermitteln folgende Abstände: |
| − | $$R_{\rm o} = 1 - 4 \cdot {\rm j}, \hspace{0.2cm}|R_{\rm o}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{1^2 + 4^2}= 4.123, \hspace{ | + | :$$R_{\rm o} = 1 - 4 \cdot {\rm j}, \hspace{0.2cm}|R_{\rm o}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{1^2 + 4^2}= 4.123, \hspace{1.15cm} |
{\rm ln} \hspace{0.1cm}|R_{\rm o}| | {\rm ln} \hspace{0.1cm}|R_{\rm o}| | ||
\hspace{0.25cm} = \hspace{0.2cm}1.417\,{\rm Np }\hspace{0.05cm},$$ | \hspace{0.25cm} = \hspace{0.2cm}1.417\,{\rm Np }\hspace{0.05cm},$$ | ||
| − | $$R_{\rm x1} = -3 - 1 \cdot {\rm | + | :$$R_{\rm x1} = -3 - 1 \cdot {\rm |
| − | j}, \hspace{0.2cm}|R_{\rm x1}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{3^2 + 1^2}= 3.162,\hspace{ | + | j}, \hspace{0.2cm}|R_{\rm x1}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{3^2 + 1^2}= 3.162,\hspace{0.5cm} |
{\rm ln} \hspace{0.1cm}|R_{\rm x1}| | {\rm ln} \hspace{0.1cm}|R_{\rm x1}| | ||
\hspace{0.25cm} = \hspace{0.2cm}1.151\,{\rm Np }\hspace{0.05cm},$$ | \hspace{0.25cm} = \hspace{0.2cm}1.151\,{\rm Np }\hspace{0.05cm},$$ | ||
| − | $$ R_{\rm x2} = -3 - 7 \cdot{\rm j}, | + | :$$ R_{\rm x2} = -3 - 7 \cdot{\rm j}, |
| − | \hspace{0.2cm}|R_{\rm x2}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{3^2 + 7^2}= 7.616,\hspace{ | + | \hspace{0.2cm}|R_{\rm x2}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{3^2 + 7^2}= 7.616,\hspace{0.5cm} |
{\rm ln} \hspace{0.1cm}|R_{\rm x2}| | {\rm ln} \hspace{0.1cm}|R_{\rm x2}| | ||
\hspace{0.25cm} = \hspace{0.2cm}2.030\,{\rm Np }\hspace{0.05cm}.$$ | \hspace{0.25cm} = \hspace{0.2cm}2.030\,{\rm Np }\hspace{0.05cm}.$$ | ||
| Zeile 138: | Zeile 141: | ||
-{\rm ln} \hspace{0.1cm} 5 | -{\rm ln} \hspace{0.1cm} 5 | ||
+ 1.151+ 2.030- | + 1.151+ 2.030- | ||
| − | 1.417=0.155\,{\rm Np } | + | 1.417\hspace{0.15cm}\underline{=0.155\,{\rm Np }} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Das entspricht $0.155\ {\rm Np} \cdot 8.686 \ {\rm dB/Np} | + | Das entspricht $0.155\ {\rm Np} \cdot 8.686 \ {\rm dB/Np} \hspace{0.15cm} \underline{= 1.346 \ {\rm dB}}$. |
| + | |||
| − | '''(4)''' Nach der | + | '''(4)''' Nach der Beschreibung im Theorieteil gilt wegen $K > 0$ für die Phasenfunktion: |
| − | $$b(f ={2}/\pi) = \phi_{\rm x1} + \phi_{\rm x2}-\phi_{\rm o}\hspace{0.05cm},$$ | + | :$$b(f ={2}/\pi) = \phi_{\rm x1} + \phi_{\rm x2}-\phi_{\rm o}\hspace{0.05cm},$$ |
| − | $$\phi_{\rm x1} ={\rm arctan}\hspace{0.15cm}(1/3) = | + | :$$\phi_{\rm x1} ={\rm arctan}\hspace{0.15cm}(1/3) = |
| − | 18.4^\circ\hspace{0.05cm}, \hspace{0. | + | 18.4^\circ\hspace{0.05cm}, \hspace{0.5cm}\phi_{\rm x2} = {\rm arctan}\hspace{0.15cm}(7/3) = |
| − | 66.8^\circ\hspace{0.05cm}, | + | 66.8^\circ\hspace{0.05cm},\hspace{0.5cm} \phi_{\rm o} = {\rm arctan}\hspace{0.15cm}(-1/4) = |
| − | + | 180^\circ - 76^\circ = 104^\circ $$ | |
| − | 180^\circ - 76^\circ = 104^\circ$$ | + | :$$ \Rightarrow \hspace{0.3cm}b(f ={2}/\pi) = |
| − | $$\Rightarrow \hspace{0.3cm}b(f ={2}/\pi) = | ||
18.4^\circ + 66.8^\circ - 104^\circ \hspace{0.15cm} \underline{= -18.8^\circ} | 18.4^\circ + 66.8^\circ - 104^\circ \hspace{0.15cm} \underline{= -18.8^\circ} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 157: | Zeile 160: | ||
| − | [[Category:Aufgaben zu Lineare zeitinvariante Systeme|^3.2 Laplace–Transformation | + | [[Category:Aufgaben zu Lineare zeitinvariante Systeme|^3.2 Laplace–Transformation^]] |
Aktuelle Version vom 14. Oktober 2021, 16:16 Uhr
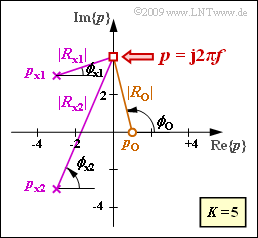
Wir gehen vom skizzierten Pol–Nullstellen–Diagramm aus, also von den Werten
- $$K = 5, \hspace{0,2cm}Z = 1, \hspace{0,2cm}N = 2, $$
- $$ p_{\rm o}= 1,\hspace{0,2cm}p_{\rm x1}= -3 + 3{\rm j},\hspace{0,2cm}p_{\rm x2}= -3 - 3{\rm j}\hspace{0.05cm} .$$
Damit lautet die $p$–Übertragungsfunktion:
- $$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$
Mit der Substitution $p = {\rm j} \cdot 2 \pi f$ lässt sich die herkömmliche Übertragungsfunktion angeben, die auch als Frequenzgang bezeichnet wird:
- $$H(f) = H_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it f}} = {\rm e}^{-a(f)\hspace{0.05cm}}\cdot {\rm e}^{- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.05cm}.$$
Aus dieser Gleichung erkennt man auch den Zusammenhang zwischen
- der Übertragungsfunktion $H(f)$,
- der Dämpfungsfunktion $a(f)$ und
- der Phasenfunktion $b(f)$.
Für eine durch den Punkt $p = {\rm j} \cdot 2 \pi f$ indirekt vorgegebene Frequenz $f$ kann man die Dämpfungs– und Phasenwerte wie folgt ermitteln:
- $$a(f)\hspace{0.15cm}{\rm in}\hspace{0.15cm}{\rm Np} \hspace{0.25cm} = \hspace{0.2cm} -{\rm ln} \hspace{0.1cm} K + {\rm ln} \hspace{0.1cm} |R_{\rm x1}|+{\rm ln} \hspace{0.1cm} |R_{\rm x1}|- {\rm ln} \hspace{0.1cm} |R_{{\rm o} }|\hspace{0.05cm} ,$$
- $$ b(f)\hspace{0.15cm}{\rm in}\hspace{0.15cm}{\rm rad} \hspace{0.25cm} = \hspace{0.2cm} \phi_{\rm x1}+ \phi_{\rm x2}-\phi_{\rm o} \hspace{0.05cm} .$$
Die entsprechenden Beträge $|R_{\rm o}|$, $|R_{\rm x1}|$ und $|R_{\rm x2}|$ können Sie ebenso wie die Winkel $\phi_{\rm o}$, $\phi_{\rm x1}$ und $\phi_{\rm x2}$ der Grafik entnehmen.
Hinweis:
- Die Aufgabe gehört zum Kapitel Laplace–Transformation und p–Übertragungsfunktion.
Fragebogen
Musterlösung
- $$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$
- Zur herkömmlichen Übertragungsfunktion (zum Frequenzgang) kommt man mit der Substitution $p = {\rm j} \cdot 2 \pi f$:
- $$H(f)= K \cdot \frac {{\rm j \hspace{0.05cm}2\pi \it f} - p_{\rm o }} {({\rm j \hspace{0.05cm}2\pi \it f} - p_{\rm x 1})({\rm j \hspace{0.05cm}2\pi \it f} - p_{\rm x 2})} = {\rm e}^{-a(f)\hspace{0.05cm}}\cdot {\rm e}^{- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.05cm} .$$
- Im Grenzfall $f → \infty$ ergibt sich für den Betrag, die Dämpfung und die Phase:
- $$\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} H(f)= \frac{K}{{\rm j \hspace{0.05cm}2\pi \it f}}\hspace{0.5cm}\Rightarrow \hspace{0.5cm}\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} |H(f)|\hspace{0.15cm}\underline {= 0} \hspace{0.5cm} \Rightarrow \hspace{0.5cm}\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} a(f)= \infty,\hspace{0.1cm} \lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} b(f)\underline {= {\pi}/{2}\hspace{0.1cm}(+90^\circ)} \hspace{0.01cm}.$$
(2) Aus der allgemeinen Gleichung in Teilaufgabe (1) erhält man mit dem Grenzübergang $f → 0$:
- $$|H(f=0)|= -\frac {K \cdot p_{\rm o }} {p_{\rm x 1}\cdot p_{\rm x 2}} = \frac {5 \cdot 1}{ (-3 + 3{\rm j})\cdot (-3 + 3{\rm j})}= \frac {5 }{18}\hspace{0.15cm}\underline {\approx 0.278} \hspace{0.05cm} ,$$
- $$a(f=0)=- {\rm ln} \hspace{0.1cm}\hspace{0.15cm}\underline { |H(f=0)|= 1.281\,{\rm Np }} \hspace{0.05cm} .$$
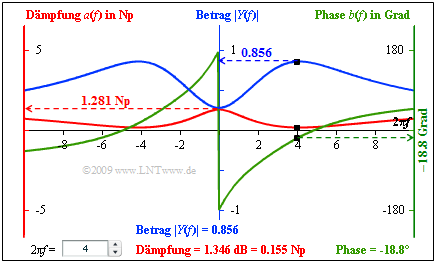
Der Bildschirmabzug des Flash–Moduls „Kausale Systeme” fasst die Ergebnisse dieser Aufgabe zusammen:
- Mittlere Achse (blau): Betrag $|H(f)|$ ⇒ hier beschriftet mit $|Y(f)|$,
- Linke Achse (rot): Dämpfung $a(f)$,
- Rechte Achse (grün): Phase $b(f)$.
- Schwarzer Punkt: Werte für $2\pi f = 4.$
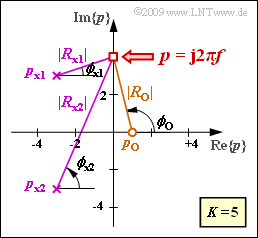
(3) Entsprechend der detaillierten Beschreibung im Theorieteil gilt für die Dämpfungsfunktion:
- $$a(f)= -{\rm ln} \hspace{0.1cm} K + {\rm ln} \hspace{0.1cm} |R_{\rm x1}|+{\rm ln} \hspace{0.1cm} |R_{\rm x2}|- {\rm ln} \hspace{0.1cm} |R_{{\rm o} }|\hspace{0.05cm} .$$
- Zu berücksichtigen ist weiterhin die Zusatzeinheit „Neper” $\rm (Np)$.
- Gesucht ist die Dämpfung bei $f = 2/\pi$. Dazu setzen wir $p = {\rm j} \cdot 2 \pi f = 4$ und ermitteln folgende Abstände:
- $$R_{\rm o} = 1 - 4 \cdot {\rm j}, \hspace{0.2cm}|R_{\rm o}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{1^2 + 4^2}= 4.123, \hspace{1.15cm} {\rm ln} \hspace{0.1cm}|R_{\rm o}| \hspace{0.25cm} = \hspace{0.2cm}1.417\,{\rm Np }\hspace{0.05cm},$$
- $$R_{\rm x1} = -3 - 1 \cdot {\rm j}, \hspace{0.2cm}|R_{\rm x1}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{3^2 + 1^2}= 3.162,\hspace{0.5cm} {\rm ln} \hspace{0.1cm}|R_{\rm x1}| \hspace{0.25cm} = \hspace{0.2cm}1.151\,{\rm Np }\hspace{0.05cm},$$
- $$ R_{\rm x2} = -3 - 7 \cdot{\rm j}, \hspace{0.2cm}|R_{\rm x2}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{3^2 + 7^2}= 7.616,\hspace{0.5cm} {\rm ln} \hspace{0.1cm}|R_{\rm x2}| \hspace{0.25cm} = \hspace{0.2cm}2.030\,{\rm Np }\hspace{0.05cm}.$$
$$\Rightarrow \hspace{0.3cm}a(f = \frac{4}{2\pi})= -{\rm ln} \hspace{0.1cm} 5 + 1.151+ 2.030- 1.417\hspace{0.15cm}\underline{=0.155\,{\rm Np }} \hspace{0.05cm}.$$
Das entspricht $0.155\ {\rm Np} \cdot 8.686 \ {\rm dB/Np} \hspace{0.15cm} \underline{= 1.346 \ {\rm dB}}$.
(4) Nach der Beschreibung im Theorieteil gilt wegen $K > 0$ für die Phasenfunktion:
- $$b(f ={2}/\pi) = \phi_{\rm x1} + \phi_{\rm x2}-\phi_{\rm o}\hspace{0.05cm},$$
- $$\phi_{\rm x1} ={\rm arctan}\hspace{0.15cm}(1/3) = 18.4^\circ\hspace{0.05cm}, \hspace{0.5cm}\phi_{\rm x2} = {\rm arctan}\hspace{0.15cm}(7/3) = 66.8^\circ\hspace{0.05cm},\hspace{0.5cm} \phi_{\rm o} = {\rm arctan}\hspace{0.15cm}(-1/4) = 180^\circ - 76^\circ = 104^\circ $$
- $$ \Rightarrow \hspace{0.3cm}b(f ={2}/\pi) = 18.4^\circ + 66.8^\circ - 104^\circ \hspace{0.15cm} \underline{= -18.8^\circ} \hspace{0.05cm}.$$