Aufgaben:Aufgabe 3.9Z: Gauß gefaltet mit Gauß: Unterschied zwischen den Versionen
Aus LNTwww
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
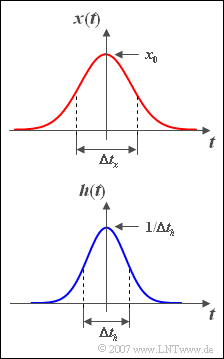
| − | [[Datei:P_ID544__Sig_Z_3_9.png|right|frame| | + | [[Datei:P_ID544__Sig_Z_3_9.png|right|frame|Gaußimpulse $x(t)$ und $h(t)$]] |
| − | Es soll das Faltungsergebnis zweier Gaußfunktionen ermittelt werden. Wir betrachten einen gaußförmigen Eingangsimpuls ${x(t)}$ mit | + | Es soll das Faltungsergebnis zweier Gaußfunktionen ermittelt werden. Wir betrachten |
| + | *einen gaußförmigen Eingangsimpuls ${x(t)}$ mit Amplitude $x_0 = 1\,\text{V}$ und äquivalenter Dauer $\Delta t_x = 4 \,\text{ms}$, sowie | ||
| + | *eine ebenfalls gaußförmige Impulsantwort ${h(t)}$, welche die äquivalente Dauer $\Delta t_h = 3 \,\text{ms}$ aufweist: | ||
:$$x( t ) = x_0 \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_x } )^2 } ,$$ | :$$x( t ) = x_0 \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_x } )^2 } ,$$ | ||
:$$h( t ) = \frac{1}{\Delta t_h } \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_h } )^2 } .$$ | :$$h( t ) = \frac{1}{\Delta t_h } \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_h } )^2 } .$$ | ||
| − | Gesucht ist das Ausgangssignal ${y(t)} = {x(t)} ∗{h(t)}$, wobei der Umweg über die Spektralfunktionen gegangen werden soll. | + | Gesucht ist das Ausgangssignal ${y(t)} = {x(t)} ∗{h(t)}$, wobei der Umweg über die Spektralfunktionen gegangen werden soll. |
| Zeile 13: | Zeile 15: | ||
| − | '' | + | ''Hinweis:'' |
| − | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltungssatz und Faltungsoperation]]. | + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltungssatz und Faltungsoperation]]. |
| − | + | ||
| Zeile 22: | Zeile 24: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie die Spektralfunktionen ${X(f)}$ und ${H(f)}$ an. Welche Werte ergeben sich für $f = 0$? | + | {Geben Sie die Spektralfunktionen ${X(f)}$ und ${H(f)}$ an. Welche Werte ergeben sich für $f = 0$? |
|type="{}"} | |type="{}"} | ||
$X(f = 0)\ = \ $ { 4 3% } $\text{mV/Hz}$ | $X(f = 0)\ = \ $ { 4 3% } $\text{mV/Hz}$ | ||
| Zeile 28: | Zeile 30: | ||
| − | {Berechnen Sie die Spektralfunktion ${Y(f)}$ des Ausgangssignals. Wie groß ist der Spektralwert bei $f = 0$? | + | {Berechnen Sie die Spektralfunktion ${Y(f)}$ des Ausgangssignals. Wie groß ist der Spektralwert bei $f = 0$? |
|type="{}"} | |type="{}"} | ||
$Y(f = 0)\ = \ $ { 4 3% } $\text{mV/Hz}$ | $Y(f = 0)\ = \ $ { 4 3% } $\text{mV/Hz}$ | ||
| − | {Berechnen Sie den Ausgangsimpuls ${y(t)}$. Welche Werte ergeben sich für die Amplitude $y_0 = y(t = 0)$ und die äquivalente Impulsdauer $\Delta t_y$? | + | {Berechnen Sie den Ausgangsimpuls ${y(t)}$. Welche Werte ergeben sich für die Amplitude $y_0 = y(t = 0)$ und die äquivalente Impulsdauer $\Delta t_y$? |
|type="{}"} | |type="{}"} | ||
$y_0\ = \ $ { 0.8 3% } $\text{V}$ | $y_0\ = \ $ { 0.8 3% } $\text{V}$ | ||
| Zeile 45: | Zeile 47: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Durch Fouriertransformation erhält man: | '''(1)''' Durch Fouriertransformation erhält man: | ||
| − | :$$X( f ) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x \cdot f} \right)^2 } , \hspace{0.5cm}H(f) = {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_h \cdot f} \right)^2 } .$$ | + | :$$X( f ) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 } , \hspace{0.5cm}H(f) = {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_h \hspace{0.05cm}\cdot \hspace{0.05cm}f} \right)^2 } .$$ |
| − | Die gesuchten Werte sind $X(f = 0)\;\underline{ = 4 \,\text{mV/Hz}}$ | + | *Die gesuchten Werte sind |
| + | :$$X(f = 0)\;\underline{ = 4 \,\text{mV/Hz}},$$ | ||
| + | :$$H(f = 0)\; \underline{= 1}.$$ | ||
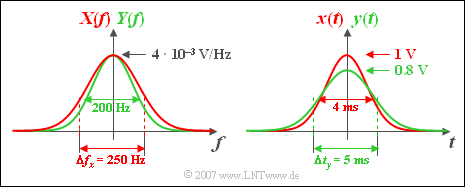
| − | [[Datei:P_ID589__Sig_Z_3_9_b_neu.png|right|frame| | + | [[Datei:P_ID589__Sig_Z_3_9_b_neu.png|right|frame|Gaußspektren $X(f)$ und $Y(f)$ – Gaußimpulse $x(t)$ und $y(t)$]] |
'''(2)''' Der Faltung im Zeitbereich entspricht die Multiplikation im Frequenzbereich: | '''(2)''' Der Faltung im Zeitbereich entspricht die Multiplikation im Frequenzbereich: | ||
:$$Y(f) = X(f) \cdot H(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x^2 + \Delta t_h^2 } \right)f^2 } .$$ | :$$Y(f) = X(f) \cdot H(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x^2 + \Delta t_h^2 } \right)f^2 } .$$ | ||
| − | Mit der Abkürzung $\Delta t_y = (\Delta t_x^2 + \Delta t_h^2)^{1/2} = 5\, \text{ms}$ kann hierfür | + | *Mit der Abkürzung $\Delta t_y = (\Delta t_x^2 + \Delta t_h^2)^{1/2} = 5\, \text{ms}$ kann man hierfür schreiben: |
| − | :$$Y(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \cdot f} \right)^2 } .$$ | + | :$$Y(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 } .$$ |
| − | *Bei der Frequenz $f = 0$ sind die Spektralwerte am Eingang und Ausgang des Gaußfilters gleich, also gilt: | + | *Bei der Frequenz $f = 0$ sind die Spektralwerte am Eingang und Ausgang des Gaußfilters gleich, also gilt: |
| − | :$$Y(f = 0) \;\underline{= 4 \text{mV/Hz}}.$$ | + | :$$Y(f = 0) \;\underline{= 4 \text{ mV/Hz}}.$$ |
| − | *Der Funktionsverlauf von ${Y(f)}$ ist schmaler als ${X(f)}$ und | + | *Der Funktionsverlauf von ${Y(f)}$ ist schmaler als ${X(f)}$ und schmaler als ${H(f)}$. |
'''(3)''' Es gilt die folgende Fourierkorrespondenz: | '''(3)''' Es gilt die folgende Fourierkorrespondenz: | ||
| − | :$${\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \cdot f} \right)^2 }\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{1}{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$ | + | :$${\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 }\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{1}{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$ |
| − | Damit erhält man: | + | *Damit erhält man: |
:$$y(t) = x(t) * h(t) = x_0 \cdot \frac{\Delta t_x }{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$ | :$$y(t) = x(t) * h(t) = x_0 \cdot \frac{\Delta t_x }{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$ | ||
| − | *Der Maximalwert des Signals ${y(t)}$ liegt ebenfalls bei $t = 0$ und beträgt $y_0 \hspace{0.15cm}\underline{= 0.8 V}$. | + | *Der Maximalwert des Signals ${y(t)}$ liegt ebenfalls bei $t = 0$ und beträgt $y_0 \hspace{0.15cm}\underline{= 0.8 \text{ V} }$. |
| − | *Die äquivalente Impulsdauer ergibt sich zu $\Delta t_y \hspace{0.15cm}\underline{= 5 \text{ms}}$ (siehe obiges | + | *Die äquivalente Impulsdauer ergibt sich zu $\Delta t_y \hspace{0.15cm}\underline{= 5 \text{ ms}}$ (siehe obiges Grafik, rechte Skizze). |
| − | *Das bedeutet: Das Gaußfilter ${H(f)}$ bewirkt, dass der Ausgangsimpuls ${y(t)}$ kleiner und breiter als der Eingangsimpuls ${x(t)}$ ist. | + | *Das bedeutet: Das Gaußfilter ${H(f)}$ bewirkt, dass der Ausgangsimpuls ${y(t)}$ kleiner und breiter als der Eingangsimpuls ${x(t)}$ ist. |
| − | *Die Impulsform bleibt weiterhin gaußförmig | + | *Die Impulsform bleibt weiterhin gaußförmig, weil: '''Gauß gefaltet mit Gauß ergibt immer Gauß!''' |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 29. April 2021, 15:29 Uhr
Es soll das Faltungsergebnis zweier Gaußfunktionen ermittelt werden. Wir betrachten
- einen gaußförmigen Eingangsimpuls ${x(t)}$ mit Amplitude $x_0 = 1\,\text{V}$ und äquivalenter Dauer $\Delta t_x = 4 \,\text{ms}$, sowie
- eine ebenfalls gaußförmige Impulsantwort ${h(t)}$, welche die äquivalente Dauer $\Delta t_h = 3 \,\text{ms}$ aufweist:
- $$x( t ) = x_0 \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_x } )^2 } ,$$
- $$h( t ) = \frac{1}{\Delta t_h } \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_h } )^2 } .$$
Gesucht ist das Ausgangssignal ${y(t)} = {x(t)} ∗{h(t)}$, wobei der Umweg über die Spektralfunktionen gegangen werden soll.
Hinweis:
- Die Aufgabe gehört zum Kapitel Faltungssatz und Faltungsoperation.
Fragebogen
Musterlösung
(1) Durch Fouriertransformation erhält man:
- $$X( f ) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 } , \hspace{0.5cm}H(f) = {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_h \hspace{0.05cm}\cdot \hspace{0.05cm}f} \right)^2 } .$$
- Die gesuchten Werte sind
- $$X(f = 0)\;\underline{ = 4 \,\text{mV/Hz}},$$
- $$H(f = 0)\; \underline{= 1}.$$
(2) Der Faltung im Zeitbereich entspricht die Multiplikation im Frequenzbereich:
- $$Y(f) = X(f) \cdot H(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x^2 + \Delta t_h^2 } \right)f^2 } .$$
- Mit der Abkürzung $\Delta t_y = (\Delta t_x^2 + \Delta t_h^2)^{1/2} = 5\, \text{ms}$ kann man hierfür schreiben:
- $$Y(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 } .$$
- Bei der Frequenz $f = 0$ sind die Spektralwerte am Eingang und Ausgang des Gaußfilters gleich, also gilt:
- $$Y(f = 0) \;\underline{= 4 \text{ mV/Hz}}.$$
- Der Funktionsverlauf von ${Y(f)}$ ist schmaler als ${X(f)}$ und schmaler als ${H(f)}$.
(3) Es gilt die folgende Fourierkorrespondenz:
- $${\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 }\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{1}{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$
- Damit erhält man:
- $$y(t) = x(t) * h(t) = x_0 \cdot \frac{\Delta t_x }{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$
- Der Maximalwert des Signals ${y(t)}$ liegt ebenfalls bei $t = 0$ und beträgt $y_0 \hspace{0.15cm}\underline{= 0.8 \text{ V} }$.
- Die äquivalente Impulsdauer ergibt sich zu $\Delta t_y \hspace{0.15cm}\underline{= 5 \text{ ms}}$ (siehe obiges Grafik, rechte Skizze).
- Das bedeutet: Das Gaußfilter ${H(f)}$ bewirkt, dass der Ausgangsimpuls ${y(t)}$ kleiner und breiter als der Eingangsimpuls ${x(t)}$ ist.
- Die Impulsform bleibt weiterhin gaußförmig, weil: Gauß gefaltet mit Gauß ergibt immer Gauß!