Aufgaben:Aufgabe 4.09Z: Laplace-verteiltes Rauschen: Unterschied zwischen den Versionen
Aus LNTwww
| (18 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | ||
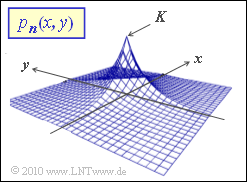
| − | [[Datei:P_ID2042__Dig_Z_4_9.png|right|frame| | + | [[Datei:P_ID2042__Dig_Z_4_9.png|right|frame|Zweidimensionale Laplace–WDF]] |
| − | Wir betrachten zweidimensionales Rauschen $\boldsymbol{n} = (n_1, n_2)$. | + | Wir betrachten zweidimensionales Rauschen $\boldsymbol{n} = (n_1, n_2)$. |
| − | Die beiden Rauschvariablen sind & | + | Die beiden Rauschvariablen sind "independent and identically distributed", abgekürzt "i.i.d.", und besitzen beide jeweils eine Laplace–Wahrscheinlichkeitsdichte: |
:$$p_{n_1}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |x|} \hspace{0.05cm},$$ | :$$p_{n_1}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |x|} \hspace{0.05cm},$$ | ||
:$$ p_{n_2}(y) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |y|} \hspace{0.05cm}. $$ | :$$ p_{n_2}(y) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |y|} \hspace{0.05cm}. $$ | ||
| − | Die | + | *Die zweidimensionale Wahrscheinlichkeitsdichtefunktion $p_{\it \boldsymbol{n}}(x, y)$ ist in der Grafik dargestellt. |
| + | |||
| + | *Zur Vereinfachung der Schreibweise werden hier die Realisierungen von $n_1$ und $n_2$ mit $x$ und $y$ bezeichnet. | ||
| − | + | ||
| − | * Die Aufgabe | + | |
| − | * | + | Hinweise: |
| − | * Weiterhin gilt: | + | * Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| "Approximation der Fehlerwahrscheinlichkeit"]]. |
| − | + | ||
| + | * Wir weisen Sie auf das interaktive SWF–Applet [[Applets:2D_Laplace|"Zweidimensionale Laplaceverteilung"]] hin. | ||
| + | |||
| + | * Das sich in Teilaufgabe '''(6)''' ergebende Integral muss aufgrund der Betragsbildung in mehrere Teilintegrale aufgespalten werden. | ||
| + | |||
| + | *Weiterhin gilt: $\int_{0}^{\infty} x^2 \cdot {\rm e}^{-a \hspace{0.03cm}\cdot \hspace{0.03cm} x} \,{\rm d} x = {2}/{a^3} \hspace{0.05cm}.$ | ||
| Zeile 21: | Zeile 28: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist die Konstante $K$ | + | {Wie groß ist die Konstante $K$ der eindimensionalen WDF? |
| − | |type=" | + | |type="()"} |
- $K = 1$. | - $K = 1$. | ||
+ $K = a/2$ | + $K = a/2$ | ||
- $K = 1/a$. | - $K = 1/a$. | ||
| − | {Es sei $a = 1$. Wie groß sind der Mittelwert ${\rm E}[n_i]$ und die Varianz $\sigma^2 = {\rm E}[n_i^2]$ der beiden | + | {Es sei $a = 1$. Wie groß sind der Mittelwert ${\rm E}\big[n_i \big]$ und die Varianz $\sigma^2 = {\rm E}\big[n_i^2\big]$ der beiden eindimensionalen Zufallsgrößen? $(i = 1,\ 2)$. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm E}[n_i]$ | + | ${\rm E}\big[n_i\big] \ = \ $ { 0. } |
| − | $ | + | ${\rm E}\big[n_i^2\big] \ = \ ${ 2 3% } |
| − | {Welche Form haben die Höhenlinien der | + | {Welche Form haben die Höhenlinien der zweidimensionalen WDF im ersten Quadranten? |
| − | |type=" | + | |type="()"} |
+ Es sind Geraden. | + Es sind Geraden. | ||
- Es sind Hyperbeln. | - Es sind Hyperbeln. | ||
- Es sind Kreise. | - Es sind Kreise. | ||
| − | {Wie groß ist die Wahrscheinlichkeit, dass sowohl $n_1$ als auch $n_2$ negativ sind? | + | {Es sei weiterhin $a = 1$. Wie groß ist die Wahrscheinlichkeit, dass sowohl $n_1$ als auch $n_2$ negativ sind? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\rm Pr}\big[(n_1 < 0) ∩ (n_2 < 0)\big]\ = \ $ { 25 3% } $\ \%$ |
| − | {Wie groß ist die Wahrscheinlichkeit, dass $n_1$ und $n_2$ jeweils größer als $1$ sind? | + | {Wie groß ist die Wahrscheinlichkeit, dass $n_1$ und $n_2$ jeweils gemeinsam größer als $1$ sind? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\rm Pr}\big[(n_1 > 1) ∩ (n_2 > 1)\big]\ = \ $ { 3.4 3% } $\ \%$ |
| − | {Wie groß ist die Wahrscheinlichkeit, dass die Summe $n_1 + n_2 > 2$ ist? | + | {Wie groß ist die Wahrscheinlichkeit, dass die Summe $n_1 + n_2 > 2$ ist? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $ {\rm Pr}\big[n_1 + n_2 > 2)\big] \ = \ $ { 13.5 3% } $\ \%$ |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Richtig ist der <u>Lösungsvorschlag 2</u>: |
| − | '''(2)''' | + | *Die Fläche unter der WDF muss $1$ ergeben: |
| − | '''(3)''' | + | :$$\int_{-\infty}^{+\infty} p_{n_1}(x) \,{\rm d} x = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |
| − | '''(4)''' | + | \int_{0}^{+\infty} p_{n_1}(x) \,{\rm d} x = 0.5 \hspace{0.3cm} |
| − | '''(5)''' | + | \Rightarrow \hspace{0.3cm} K \cdot \int_{0}^{\infty} {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}x} \,{\rm d} x = - {K}/{a} \cdot \left [ {\rm e}^{- a \hspace{0.03cm} \cdot \hspace{0.03cm} x} |
| + | \right ]_{0}^{\infty}= {K}/{a} = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K = {a}/{2}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' Der <u>lineare Mittelwert</u> ist aufgrund der WDF–Symmetrie <u>gleich 0</u>. | ||
| + | |||
| + | *Damit ist die Varianz $\sigma^2$ tatsächlich – wie bereits in der Fragestellung angegeben – gleich dem zweiten Erwartungswert: | ||
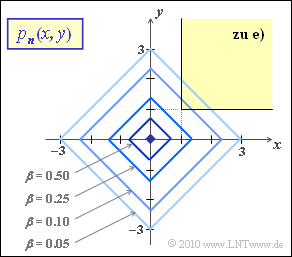
| + | [[Datei:P_ID2045__Dig_Z_4_9c.png|right|frame|Höhenlinien der zweidimensionalen Laplaceverteilung]] | ||
| + | :$$\sigma^2 = {\rm E}[n_1^2] = 2 \cdot \frac{a}{2} \cdot \int_{0}^{\infty} x^2 \cdot {\rm e}^{-a \hspace{0.03cm} \cdot \hspace{0.03cm} x} \,{\rm d} x = a \cdot {2}/{a^3}= | ||
| + | {2}/{a^2} \hspace{0.05cm}. \hspace{0.2cm}{\rm Mit}\hspace{0.15cm}a = 1\text{:} \hspace{0.2cm}\hspace{0.1cm}\underline {\sigma^2 = 2 }\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Richtig ist der <u>Lösungsvorschlag 1</u>: | ||
| + | *Im ersten Quadranten $(x ≥ 0, y ≥ 0)$ kann auf die Betragsbildung verzichtet werden. Dann gilt für die 2D–WDF: | ||
| + | :$$\boldsymbol{ p }_{\boldsymbol{ n }} (x,\hspace{0.15cm} y) = {a^2}/{4} \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}x} \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}y }= {a^2}/{4} \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}(x+y)}\hspace{0.05cm}.$$ | ||
| + | *Eine Höhenlinie mit dem Faktor $\beta$ gegenüber dem Maximum hat dann den folgenden Verlauf $(0 < \beta < 1)$: | ||
| + | :$${\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}(x+y)} = \beta | ||
| + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x + y = \frac{{\rm ln}\hspace{0.15cm}1/\beta}{a} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Die Grafik zeigt die Höhenlinien für $a = 1$ und einige Werte von $\beta$, die jeweils ein um $45^\circ$ gedrehtes Quadrat ergeben ⇒ die Höhenlinien sind also Gerade. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Das hier betrachtete Wahrscheinlichkeitsereignis entspricht genau dem dritten Quadranten der oben skizzierten Verbund–WDF. Aufgrund der Symmetrie ist diese Wahrscheinlichkeit: | ||
| + | :$${\rm Pr}[(n_1 < 0) ∩ (n_2 < 0)]\hspace{0.15cm}\underline {=25\%}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Dafür kann mit der Verbund–WDF geschrieben werden: | ||
| + | :$${\rm Pr} \left [ (n_1 > 1)\cap (n_2 > 1)\right ] = {1}/{4} \cdot \int_{1}^{\infty} \int_{1}^{\infty}{\rm e}^{- (x+y)} \,{\rm d} x \,{\rm d} y == {1}/{2} \cdot \int_{1}^{\infty} {\rm e}^{- x} \,{\rm d} x \hspace{0.15cm} \cdot \hspace{0.15cm} | ||
| + | {1}/{2} \cdot \int_{1}^{\infty} {\rm e}^{- y} \,{\rm d} y $$ | ||
| + | :$$ \Rightarrow \hspace{0.3cm}{\rm Pr} \left [ (n_1 > 1)\cap (n_2 > 1)\right ] = \left [ {\rm Pr} (n_1 > 1)\right ] \cdot \left [ {\rm Pr} (n_2 > 1)\right ]\hspace{0.05cm}. $$ | ||
| + | |||
| + | *Berücksichtigt ist die statistische Unabhängigkeit zwischen $n_1$ und $n_2$ sowie die Gleichheit $p_{\it n1}(x) = p_{\it n2}(y)$. Für $a = 1$ gilt: | ||
| + | :$${\rm Pr} (n_1 > 1) = {1}/{2} \cdot \int_{1}^{\infty} {\rm e}^{- x} \,{\rm d} x = {1}/({2{\rm e}})\approx 0.184\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} {\rm Pr} \left [ (n_1 > 1)\cap (n_2 > 1)\right ] = {1}/({4{\rm e}^2)}\hspace{0.1cm}\hspace{0.15cm}\underline {\approx 3.4\%}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
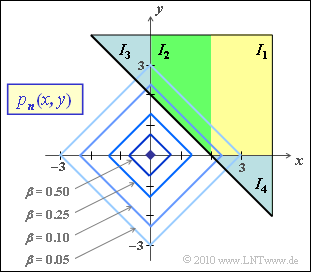
| + | [[Datei:P_ID2046__Dig_Z_4_9f.png|right|frame|Aufteilung des Integrationsbereichs]] | ||
| + | '''(6)''' Die hier betrachtete Region ist in der rechten Grafik farbig markiert. | ||
| + | *Die Regionen erstrecken sich aber nach rechts und oben bis ins Unendliche. | ||
| + | *Die gesuchte Wahrscheinlichkeit ergibt sich zu | ||
| + | |||
| + | :$${\rm Pr} [ n_1 \hspace{-0.2cm} \ + \ \hspace{-0.2cm} n_2 > 2 ] =\frac{1}{4} \cdot \int\limits_{-\infty}^{+\infty} {\rm e}^{-|x|} \int\limits_{2-x}^{\infty}{\rm e}^{-|y|} \,{\rm d} y \,{\rm d} x = I_1 + I_2 + I_3 + I_4 \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Aufgrund der Betragsbildung ist eine Aufspaltung in Teilintegrale vorzunehmen. | ||
| + | *Nach oben und rechts erstrecken sich alle Gebiete bis ins Unendliche. | ||
| + | *Aufgrund der Symmetrie gilt $I_4 = I_3$. | ||
| + | :$$I_1 = {1}/{4} \cdot \int_{2}^{+\infty} \hspace{-0.15cm}{\rm e}^{-x} \int_{0}^{\infty}\hspace{-0.15cm}{\rm e}^{-y} \,{\rm d} y \,{\rm d} x = | ||
| + | {1}/{4} \cdot \int_{2}^{+\infty} {\rm e}^{-x} \,{\rm d} x ={1}/({4{\rm e}^2})\hspace{0.05cm},$$ | ||
| + | :$$I_2 = {1}/{4} \cdot \hspace{-0.1cm} \int_{0}^{2} \hspace{-0.15cm}{\rm e}^{-x} \int_{2-x}^{\infty}\hspace{-0.15cm}{\rm e}^{-y} \,{\rm d} y \,{\rm d} x = | ||
| + | {1}/{4} \cdot \hspace{-0.1cm} \int_{0}^{2} {\rm e}^{-x}\hspace{-0.1cm} \cdot {\rm e}^{x-2} \,{\rm d} x$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}I_2 = {1}/{4} \cdot \hspace{-0.1cm}\int_{0}^{2} {\rm e}^{-2} \,{\rm d} x | ||
| + | = {1}/({2{\rm e}^2})\hspace{0.05cm},$$ | ||
| + | :$$I_3 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{x} \int_{2-x}^{\infty}{\rm e}^{-y} \,{\rm d} y \,{\rm d} x = | ||
| + | {1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{x} \cdot {\rm e}^{x-2} \,{\rm d} x | ||
| + | = {1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{2x-2} \,{\rm d} x = \frac{{\rm e}^{-2}}{4} \cdot \int_{0}^{\infty} {\rm e}^{-2x} \,{\rm d} x | ||
| + | = {1}/({8{\rm e}^2})\hspace{0.05cm},$$ | ||
| + | :$$I_4 ={1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{y} \int_{2-y}^{\infty}{\rm e}^{-x} \,{\rm d} x \,{\rm d} y = ... = | ||
| + | {1}/({8{\rm e}^2}) = I_3\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Insgesamt ergibt sich somit: | ||
| + | :$${\rm Pr} \left [ n_1 + n_2 > 2 \right ] = {\rm e}^{-2} \cdot ({1}/{4} +{1}/{2} +{1}/{8} +{1}/{8})= {\rm e}^{-2} \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 13.5\%}\hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 30. Juli 2022, 14:27 Uhr
Wir betrachten zweidimensionales Rauschen $\boldsymbol{n} = (n_1, n_2)$.
Die beiden Rauschvariablen sind "independent and identically distributed", abgekürzt "i.i.d.", und besitzen beide jeweils eine Laplace–Wahrscheinlichkeitsdichte:
- $$p_{n_1}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |x|} \hspace{0.05cm},$$
- $$ p_{n_2}(y) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |y|} \hspace{0.05cm}. $$
- Die zweidimensionale Wahrscheinlichkeitsdichtefunktion $p_{\it \boldsymbol{n}}(x, y)$ ist in der Grafik dargestellt.
- Zur Vereinfachung der Schreibweise werden hier die Realisierungen von $n_1$ und $n_2$ mit $x$ und $y$ bezeichnet.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Approximation der Fehlerwahrscheinlichkeit".
- Wir weisen Sie auf das interaktive SWF–Applet "Zweidimensionale Laplaceverteilung" hin.
- Das sich in Teilaufgabe (6) ergebende Integral muss aufgrund der Betragsbildung in mehrere Teilintegrale aufgespalten werden.
- Weiterhin gilt: $\int_{0}^{\infty} x^2 \cdot {\rm e}^{-a \hspace{0.03cm}\cdot \hspace{0.03cm} x} \,{\rm d} x = {2}/{a^3} \hspace{0.05cm}.$
Fragebogen
Musterlösung
(1) Richtig ist der Lösungsvorschlag 2:
- Die Fläche unter der WDF muss $1$ ergeben:
- $$\int_{-\infty}^{+\infty} p_{n_1}(x) \,{\rm d} x = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \int_{0}^{+\infty} p_{n_1}(x) \,{\rm d} x = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K \cdot \int_{0}^{\infty} {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}x} \,{\rm d} x = - {K}/{a} \cdot \left [ {\rm e}^{- a \hspace{0.03cm} \cdot \hspace{0.03cm} x} \right ]_{0}^{\infty}= {K}/{a} = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K = {a}/{2}\hspace{0.05cm}.$$
(2) Der lineare Mittelwert ist aufgrund der WDF–Symmetrie gleich 0.
- Damit ist die Varianz $\sigma^2$ tatsächlich – wie bereits in der Fragestellung angegeben – gleich dem zweiten Erwartungswert:
- $$\sigma^2 = {\rm E}[n_1^2] = 2 \cdot \frac{a}{2} \cdot \int_{0}^{\infty} x^2 \cdot {\rm e}^{-a \hspace{0.03cm} \cdot \hspace{0.03cm} x} \,{\rm d} x = a \cdot {2}/{a^3}= {2}/{a^2} \hspace{0.05cm}. \hspace{0.2cm}{\rm Mit}\hspace{0.15cm}a = 1\text{:} \hspace{0.2cm}\hspace{0.1cm}\underline {\sigma^2 = 2 }\hspace{0.05cm}.$$
(3) Richtig ist der Lösungsvorschlag 1:
- Im ersten Quadranten $(x ≥ 0, y ≥ 0)$ kann auf die Betragsbildung verzichtet werden. Dann gilt für die 2D–WDF:
- $$\boldsymbol{ p }_{\boldsymbol{ n }} (x,\hspace{0.15cm} y) = {a^2}/{4} \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}x} \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}y }= {a^2}/{4} \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}(x+y)}\hspace{0.05cm}.$$
- Eine Höhenlinie mit dem Faktor $\beta$ gegenüber dem Maximum hat dann den folgenden Verlauf $(0 < \beta < 1)$:
- $${\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}(x+y)} = \beta \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x + y = \frac{{\rm ln}\hspace{0.15cm}1/\beta}{a} \hspace{0.05cm}.$$
- Die Grafik zeigt die Höhenlinien für $a = 1$ und einige Werte von $\beta$, die jeweils ein um $45^\circ$ gedrehtes Quadrat ergeben ⇒ die Höhenlinien sind also Gerade.
(4) Das hier betrachtete Wahrscheinlichkeitsereignis entspricht genau dem dritten Quadranten der oben skizzierten Verbund–WDF. Aufgrund der Symmetrie ist diese Wahrscheinlichkeit:
- $${\rm Pr}[(n_1 < 0) ∩ (n_2 < 0)]\hspace{0.15cm}\underline {=25\%}.$$
(5) Dafür kann mit der Verbund–WDF geschrieben werden:
- $${\rm Pr} \left [ (n_1 > 1)\cap (n_2 > 1)\right ] = {1}/{4} \cdot \int_{1}^{\infty} \int_{1}^{\infty}{\rm e}^{- (x+y)} \,{\rm d} x \,{\rm d} y == {1}/{2} \cdot \int_{1}^{\infty} {\rm e}^{- x} \,{\rm d} x \hspace{0.15cm} \cdot \hspace{0.15cm} {1}/{2} \cdot \int_{1}^{\infty} {\rm e}^{- y} \,{\rm d} y $$
- $$ \Rightarrow \hspace{0.3cm}{\rm Pr} \left [ (n_1 > 1)\cap (n_2 > 1)\right ] = \left [ {\rm Pr} (n_1 > 1)\right ] \cdot \left [ {\rm Pr} (n_2 > 1)\right ]\hspace{0.05cm}. $$
- Berücksichtigt ist die statistische Unabhängigkeit zwischen $n_1$ und $n_2$ sowie die Gleichheit $p_{\it n1}(x) = p_{\it n2}(y)$. Für $a = 1$ gilt:
- $${\rm Pr} (n_1 > 1) = {1}/{2} \cdot \int_{1}^{\infty} {\rm e}^{- x} \,{\rm d} x = {1}/({2{\rm e}})\approx 0.184\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr} \left [ (n_1 > 1)\cap (n_2 > 1)\right ] = {1}/({4{\rm e}^2)}\hspace{0.1cm}\hspace{0.15cm}\underline {\approx 3.4\%}\hspace{0.05cm}.$$
(6) Die hier betrachtete Region ist in der rechten Grafik farbig markiert.
- Die Regionen erstrecken sich aber nach rechts und oben bis ins Unendliche.
- Die gesuchte Wahrscheinlichkeit ergibt sich zu
- $${\rm Pr} [ n_1 \hspace{-0.2cm} \ + \ \hspace{-0.2cm} n_2 > 2 ] =\frac{1}{4} \cdot \int\limits_{-\infty}^{+\infty} {\rm e}^{-|x|} \int\limits_{2-x}^{\infty}{\rm e}^{-|y|} \,{\rm d} y \,{\rm d} x = I_1 + I_2 + I_3 + I_4 \hspace{0.05cm}.$$
- Aufgrund der Betragsbildung ist eine Aufspaltung in Teilintegrale vorzunehmen.
- Nach oben und rechts erstrecken sich alle Gebiete bis ins Unendliche.
- Aufgrund der Symmetrie gilt $I_4 = I_3$.
- $$I_1 = {1}/{4} \cdot \int_{2}^{+\infty} \hspace{-0.15cm}{\rm e}^{-x} \int_{0}^{\infty}\hspace{-0.15cm}{\rm e}^{-y} \,{\rm d} y \,{\rm d} x = {1}/{4} \cdot \int_{2}^{+\infty} {\rm e}^{-x} \,{\rm d} x ={1}/({4{\rm e}^2})\hspace{0.05cm},$$
- $$I_2 = {1}/{4} \cdot \hspace{-0.1cm} \int_{0}^{2} \hspace{-0.15cm}{\rm e}^{-x} \int_{2-x}^{\infty}\hspace{-0.15cm}{\rm e}^{-y} \,{\rm d} y \,{\rm d} x = {1}/{4} \cdot \hspace{-0.1cm} \int_{0}^{2} {\rm e}^{-x}\hspace{-0.1cm} \cdot {\rm e}^{x-2} \,{\rm d} x$$
- $$\Rightarrow \hspace{0.3cm}I_2 = {1}/{4} \cdot \hspace{-0.1cm}\int_{0}^{2} {\rm e}^{-2} \,{\rm d} x = {1}/({2{\rm e}^2})\hspace{0.05cm},$$
- $$I_3 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{x} \int_{2-x}^{\infty}{\rm e}^{-y} \,{\rm d} y \,{\rm d} x = {1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{x} \cdot {\rm e}^{x-2} \,{\rm d} x = {1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{2x-2} \,{\rm d} x = \frac{{\rm e}^{-2}}{4} \cdot \int_{0}^{\infty} {\rm e}^{-2x} \,{\rm d} x = {1}/({8{\rm e}^2})\hspace{0.05cm},$$
- $$I_4 ={1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{y} \int_{2-y}^{\infty}{\rm e}^{-x} \,{\rm d} x \,{\rm d} y = ... = {1}/({8{\rm e}^2}) = I_3\hspace{0.05cm}.$$
- Insgesamt ergibt sich somit:
- $${\rm Pr} \left [ n_1 + n_2 > 2 \right ] = {\rm e}^{-2} \cdot ({1}/{4} +{1}/{2} +{1}/{8} +{1}/{8})= {\rm e}^{-2} \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 13.5\%}\hspace{0.05cm}.$$