Aufgaben:Aufgabe 4.2Z: Achtstufiges Phase Shift Keying: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Signale, Basisfunktionen und Vektorräume}} Datei:P_ID1998__Dig_Z_4_2.png|right|frame|Signalraumpunkte be…“) |
|||
| (16 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
[[Datei:P_ID1998__Dig_Z_4_2.png|right|frame|Signalraumpunkte bei 8-PSK]] | [[Datei:P_ID1998__Dig_Z_4_2.png|right|frame|Signalraumpunkte bei 8-PSK]] | ||
| − | Die $M = 8$ möglichen Sendesignale bei 8–PSK lauten mit $i = 0, \ ... \ , 7$ im Bereich $0 ≤ t < T$: | + | Die $M = 8$ möglichen Sendesignale bei 8–PSK lauten mit $i = 0, \ \text{...} \ , 7$ im Bereich $0 ≤ t < T$: |
:$$s_i(t)= A \cdot \cos(2\pi f_{\rm T}t + i \cdot {\pi}/{4}) \hspace{0.05cm}.$$ | :$$s_i(t)= A \cdot \cos(2\pi f_{\rm T}t + i \cdot {\pi}/{4}) \hspace{0.05cm}.$$ | ||
| − | Außerhalb der Symboldauer $T$ sind die Signale $s_i(t)$ alle | + | Außerhalb der Symboldauer $T$ sind die Signale $s_i(t)$ alle Null. |
| − | In der [[Aufgaben:4.2_AM/PM-Schwingungen| Aufgabe | + | In der [[Aufgaben:4.2_AM/PM-Schwingungen| Aufgabe 4.2]] wurde gezeigt, dass diese Signalmenge durch die Basisfunktionen |
:$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},$$ | :$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},$$ | ||
:$$\varphi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}$$ | :$$\varphi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}$$ | ||
| − | wie folgt dargestellt werden kann ( | + | wie folgt dargestellt werden kann $(i = 0, \ \text{...} \ , 7)$: |
:$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}.$$ | :$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}.$$ | ||
| − | Die äquivalente Tiefpassdarstellung der Signale $s_i(t)$ lautet | + | Die äquivalente Tiefpassdarstellung der Signale $s_i(t)$ lautet entsprechend dem Abschnitt [[Modulationsverfahren/Quadratur%E2%80%93Amplitudenmodulation#Systembeschreibung_durch_das_.C3.A4quivalente_Tiefpass.E2.80.93Signal| "Systembeschreibung durch das äquivalente Tiefpass–Signal"]] des Buches „Modulationsverfahren”: |
:$$s_{{\rm TP}i}(t)= a_{i} \cdot g_s(t) \hspace{0.05cm}, \hspace{0.2cm}a_{i} = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i} | :$$s_{{\rm TP}i}(t)= a_{i} \cdot g_s(t) \hspace{0.05cm}, \hspace{0.2cm}a_{i} = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i} | ||
| − | \hspace{0.05cm}, \hspace{0.2cm}i = 0, ... \hspace{0.1cm} , 7 \hspace{0.05cm},$$ | + | \hspace{0.05cm}, \hspace{0.2cm}i = 0,\text{...} \hspace{0.1cm} , 7 \hspace{0.05cm},$$ |
| − | wobei $a_i$ komplexe dimensionslose Koeffizienten sind und die Energie des Sendegrundimpulses $g_s(t)$ im Tiefpassbereich $E_{\it | + | wobei $a_i$ komplexe dimensionslose Koeffizienten sind und die Energie des Sendegrundimpulses $g_s(t)$ im Tiefpassbereich $E_{\it g_s}$ beträgt. Im hier dargestellten Fall beschreibt $g_s(t)$ einen Rechteckimpuls, doch kann für $g_s(t)$ auch ein jeder andere energiebegrenzte Impuls verwendet werden. |
| − | Die Grafik zeigt die Signalraumdarstellung der 8–PSK für das Bandpass–Signal (oben) sowie für das äquivalente Tiefpass–Signal (unten) | + | Die Grafik zeigt die Signalraumdarstellung der 8–PSK für das Bandpass–Signal (oben) sowie für das äquivalente Tiefpass–Signal (unten): |
| + | *Man erkennt daraus, dass sich die beiden Darstellungen nur duch die verwendeten Basisfunktionen unterscheiden, wobei $\varphi_1(t)$ in der oberen und der unteren Grafik für unterschiedliche Funktionen steht. | ||
| + | |||
| + | *In der Tiefpassdarstellung gilt $\varphi_2(t) = {\rm j} \cdot \varphi_1(t)$. | ||
| − | + | ||
| − | * Die Aufgabe gehört zum | + | |
| − | * Im Gegensatz zum Theorieteil und zur [[Aufgaben:4.2_AM/PM-Schwingungen| Aufgabe | + | |
| − | + | Hinweise: | |
| − | + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Signale,_Basisfunktionen_und_Vektorr%C3%A4ume| "Signale, Basisfunktionen und Vektorräume"]]. | |
| + | |||
| + | * Verwenden Sie zur Abkürzung die Energie $E = 1/2 \cdot A^2 \cdot T$. | ||
| + | |||
| + | * Im Gegensatz zum Theorieteil und zur [[Aufgaben:4.2_AM/PM-Schwingungen| "Aufgabe 4.2"]] kann hier die Laufvariable $i$ die Werte $0, \ \text{...} \, ,M-1$ annehmen. | ||
| + | |||
| + | *Auf die farblich markierten Signalraumpunkte in der Grafik (blau, rot, grün) wird im Fragebogen Bezug genommen. Diese sehen für die Signale $s_0(t)$, $s_2(t)$ und $s_5(t)$. | ||
| Zeile 33: | Zeile 42: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie lauten die Koeffizienten des Signals $s_0(t)$? |
| + | |type="{}"} | ||
| + | $s_{\rm 01} \ = \ $ { 1 3% } $\ \cdot \sqrt{E}$ | ||
| + | $s_{\rm 02} \ = \ $ { 0. } $\ \cdot \sqrt{E}$ | ||
| + | |||
| + | {Wie lauten die Koeffizienten des Signals $s_2(t)$? | ||
| + | |type="{}"} | ||
| + | $s_{\rm 21} \ = \ $ { 0. } $\ \cdot \sqrt{E}$ | ||
| + | $s_{\rm 22} \ = \ $ { 1 3% } $\ \cdot \sqrt{E}$ | ||
| + | |||
| + | {Wie lauten die Koeffizienten des Signals $s_5(t)$? | ||
| + | |type="{}"} | ||
| + | $s_{\rm 51} \ = \ $ { -0.72821--0.68579 } $\ \cdot \sqrt{E}$ | ||
| + | $s_{\rm 52} \ = \ $ { -0.72821--0.68579 } $\ \cdot \sqrt{E}$ | ||
| + | |||
| + | {Durch welche Basisfunktionen sind die Tiefpass–Signale $s_{\rm TP \it i}(t)$ darstellbar? Durch | ||
|type="[]"} | |type="[]"} | ||
| − | + | + | + eine komplexe Basisfunktion $\xi_1(t)$, |
| − | - | + | - zwei komplexe Basisfunktionen $\xi_1(t)$ und $\xi_2(t)$, |
| + | + zwei reelle Funktionen $\varphi_1(t)$ und $\psi_1(t)$. | ||
| − | { | + | {Wie lauten im vorliegenden Fall die reellen Basisfunktionen? |
| − | |type="{} | + | |type="[]"} |
| − | $ | + | - $\varphi_1(t) = g_s(t)$, |
| + | + $\varphi_1(t) = g_s(t)/\sqrt{E_{\rm g_s}}$, | ||
| + | + $\psi_1(t) = \varphi_1(t)$, | ||
| + | - $\psi_1(t) = {\rm j} \cdot \varphi_1(t)$. | ||
| + | |||
| + | {Es gelte $s_{\rm TP0}(t) = \sqrt{E}$. Was trifft zu? | ||
| + | |type="()"} | ||
| + | - Die Energie $E$ bezieht sich auf das Tiefpass–Signal. | ||
| + | + Die Energie $E$ bezieht sich auf das Bandpass–Signal. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Das Signal $s_0(t)$ lautet: |
| − | '''(2)''' | + | :$$s_0(t)= A \cdot \cos(2\pi f_{\rm T}t ) = s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm}.$$ |
| − | '''(3)''' | + | |
| − | '''(4)''' | + | *Da dieses Signal keinen Sinusteil aufweist, ist $s_{\rm 02} \hspace{0.15cm}\underline {= 0}$. |
| − | '''(5)''' | + | |
| + | *Weiter gilt mit der angegebenen Abkürzung: | ||
| + | :$$A = s_{01} \cdot \sqrt{{2}/{T}}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | s_{01}=\sqrt{1/2 \cdot A^2 \cdot T} = \sqrt{E}\hspace{0.05cm} \hspace{0.15cm}\underline { = 1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' Das Signal $s_2(t)$ lautet mit $i = 2$ $($beachten Sie, dass die zweite Basisfunktion minus–sinusförmig ist$)$: | ||
| + | :$$s_2(t)= A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{2})= - A \cdot \sin(2\pi f_{\rm T}t )\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} s_{21}\hspace{0.05cm} \underline{= 0}\hspace{0.05cm}, \hspace{0.2cm} s_{22}= \sqrt{E} \hspace{0.05cm} \hspace{0.15cm}\underline {=1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Entsprechend den Musterlösungen zu den Teilaufgaben '''(1)''' und '''(2)''' gilt nun: | ||
| + | :$$s_{51}= s_{52}= - \sqrt{E/2} \hspace{0.05cm} \hspace{0.15cm}\underline { = -0.707 \cdot E^{\hspace{0.05cm}0.5}}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} s_{5}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - {A}/{ \sqrt{2}} \cdot \cos(2\pi f_{\rm T}t ) - {A}/{ \sqrt{2}} \cdot \sin(2\pi f_{\rm T}t )=A \cdot \cos(2\pi f_{\rm T}t + \phi_5)\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\phi_5 = -0.75 \cdot \pi | ||
| + | \hspace{0.2cm}{\rm bzw.}\hspace{0.2cm}\phi_5 = 1.25 \cdot \pi | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>. | ||
| + | *Dabei gilt folgender Zusammenhang: | ||
| + | :$$\xi_1 (t) = \varphi_1 (t) + {\rm j} \cdot \psi_1 (t)\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' Richtig sind die <u>Alternativen 2 und 3</u>: | ||
| + | *Die Basisfunktion muss energienormiert sein. | ||
| + | * $\psi_1(t)$ ist wie $\varphi_1(t)$ eine reelle, nicht etwa eine imaginäre Funktion: | ||
| + | :$$\varphi_1 (t) = \psi_1 (t) = | ||
| + | \left\{ \begin{array}{c} 1/\sqrt{T} \\ | ||
| + | 0 \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | ||
| + | \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$ | ||
| + | |||
| + | |||
| + | '''(6)''' Aus dem Tiefpass–Signal $s_{\rm TP0}(t)$ kann man auch das Bandpass–Signal $s_0(t)$ berechnen. | ||
| + | *Im Bereich $0 ≤ t ≤ T$ erhält man mit dem Ergebnis aus '''(5)''' das gleiche Ergebnis wie in der Teilaufgabe '''(1)''' : | ||
| + | :$$s_0(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\left[s_{{\rm TP}0}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \right] | ||
| + | = {\rm Re}\left[\sqrt{E} /{\sqrt{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \right]= \sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t ) | ||
| + | \hspace{0.05cm},$$ | ||
| + | |||
| + | *Daraus folgt: Die Energie $E$ bezieht sich auch bei Betrachtung im äquivalenten Tiefpass–Bereich auf das Bandpass–Signal. | ||
| + | |||
| + | *Entsprechend gilt für das mit blauem Punkt markierte Signal $s_2(t)$ im interessierenden Bereich: | ||
| + | :$$s_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\big[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \big] | ||
| + | = {\rm Re}\big[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t)- \sqrt{E/T} \cdot \sin(2\pi f_{\rm T}t) \big] | ||
| + | = - \sqrt{E/T} \cdot \sin(2\pi f_{\rm T}t) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Schließlich kann für das (grüne) Signal $s_5(t)$ im Bereich $0 ≤ t < T$ geschrieben werden: | ||
| + | :$$s_5(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\big[\frac{-1 - {\rm j}}{\sqrt{2}} \cdot \sqrt{{E}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \big] = \text{...} | ||
| + | = - \sqrt{\frac{E}{2T}} \cdot \cos(2\pi f_{\rm T}t)+ \sqrt{\frac{E}{2T}} \cdot \sin(2\pi f_{\rm T}t)=\sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t + 1.25 \cdot \pi) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Auch diese Ergebnisse stimmen mit denen der Teilaufgaben '''(2)''' bzw. '''(3)''' überein. Zutreffend ist also der <u>Lösungsvorschlag 2</u>. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Digitalsignalübertragung|^4.1 | + | [[Category:Aufgaben zu Digitalsignalübertragung|^4.1 Basisfunktionen & Vektorräume^]] |
Aktuelle Version vom 13. Juli 2022, 17:33 Uhr
Die $M = 8$ möglichen Sendesignale bei 8–PSK lauten mit $i = 0, \ \text{...} \ , 7$ im Bereich $0 ≤ t < T$:
- $$s_i(t)= A \cdot \cos(2\pi f_{\rm T}t + i \cdot {\pi}/{4}) \hspace{0.05cm}.$$
Außerhalb der Symboldauer $T$ sind die Signale $s_i(t)$ alle Null.
In der Aufgabe 4.2 wurde gezeigt, dass diese Signalmenge durch die Basisfunktionen
- $$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},$$
- $$\varphi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}$$
wie folgt dargestellt werden kann $(i = 0, \ \text{...} \ , 7)$:
- $$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}.$$
Die äquivalente Tiefpassdarstellung der Signale $s_i(t)$ lautet entsprechend dem Abschnitt "Systembeschreibung durch das äquivalente Tiefpass–Signal" des Buches „Modulationsverfahren”:
- $$s_{{\rm TP}i}(t)= a_{i} \cdot g_s(t) \hspace{0.05cm}, \hspace{0.2cm}a_{i} = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i} \hspace{0.05cm}, \hspace{0.2cm}i = 0,\text{...} \hspace{0.1cm} , 7 \hspace{0.05cm},$$
wobei $a_i$ komplexe dimensionslose Koeffizienten sind und die Energie des Sendegrundimpulses $g_s(t)$ im Tiefpassbereich $E_{\it g_s}$ beträgt. Im hier dargestellten Fall beschreibt $g_s(t)$ einen Rechteckimpuls, doch kann für $g_s(t)$ auch ein jeder andere energiebegrenzte Impuls verwendet werden.
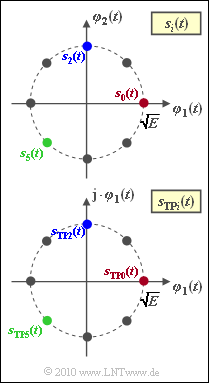
Die Grafik zeigt die Signalraumdarstellung der 8–PSK für das Bandpass–Signal (oben) sowie für das äquivalente Tiefpass–Signal (unten):
- Man erkennt daraus, dass sich die beiden Darstellungen nur duch die verwendeten Basisfunktionen unterscheiden, wobei $\varphi_1(t)$ in der oberen und der unteren Grafik für unterschiedliche Funktionen steht.
- In der Tiefpassdarstellung gilt $\varphi_2(t) = {\rm j} \cdot \varphi_1(t)$.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Signale, Basisfunktionen und Vektorräume".
- Verwenden Sie zur Abkürzung die Energie $E = 1/2 \cdot A^2 \cdot T$.
- Im Gegensatz zum Theorieteil und zur "Aufgabe 4.2" kann hier die Laufvariable $i$ die Werte $0, \ \text{...} \, ,M-1$ annehmen.
- Auf die farblich markierten Signalraumpunkte in der Grafik (blau, rot, grün) wird im Fragebogen Bezug genommen. Diese sehen für die Signale $s_0(t)$, $s_2(t)$ und $s_5(t)$.
Fragebogen
Musterlösung
- $$s_0(t)= A \cdot \cos(2\pi f_{\rm T}t ) = s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm}.$$
- Da dieses Signal keinen Sinusteil aufweist, ist $s_{\rm 02} \hspace{0.15cm}\underline {= 0}$.
- Weiter gilt mit der angegebenen Abkürzung:
- $$A = s_{01} \cdot \sqrt{{2}/{T}}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} s_{01}=\sqrt{1/2 \cdot A^2 \cdot T} = \sqrt{E}\hspace{0.05cm} \hspace{0.15cm}\underline { = 1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$
(2) Das Signal $s_2(t)$ lautet mit $i = 2$ $($beachten Sie, dass die zweite Basisfunktion minus–sinusförmig ist$)$:
- $$s_2(t)= A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{2})= - A \cdot \sin(2\pi f_{\rm T}t )\hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{21}\hspace{0.05cm} \underline{= 0}\hspace{0.05cm}, \hspace{0.2cm} s_{22}= \sqrt{E} \hspace{0.05cm} \hspace{0.15cm}\underline {=1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$
(3) Entsprechend den Musterlösungen zu den Teilaufgaben (1) und (2) gilt nun:
- $$s_{51}= s_{52}= - \sqrt{E/2} \hspace{0.05cm} \hspace{0.15cm}\underline { = -0.707 \cdot E^{\hspace{0.05cm}0.5}}$$
- $$\Rightarrow \hspace{0.3cm} s_{5}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - {A}/{ \sqrt{2}} \cdot \cos(2\pi f_{\rm T}t ) - {A}/{ \sqrt{2}} \cdot \sin(2\pi f_{\rm T}t )=A \cdot \cos(2\pi f_{\rm T}t + \phi_5)\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\phi_5 = -0.75 \cdot \pi \hspace{0.2cm}{\rm bzw.}\hspace{0.2cm}\phi_5 = 1.25 \cdot \pi \hspace{0.05cm}.$$
(4) Richtig sind die Lösungsvorschläge 1 und 3.
- Dabei gilt folgender Zusammenhang:
- $$\xi_1 (t) = \varphi_1 (t) + {\rm j} \cdot \psi_1 (t)\hspace{0.05cm}.$$
(5) Richtig sind die Alternativen 2 und 3:
- Die Basisfunktion muss energienormiert sein.
- $\psi_1(t)$ ist wie $\varphi_1(t)$ eine reelle, nicht etwa eine imaginäre Funktion:
- $$\varphi_1 (t) = \psi_1 (t) = \left\{ \begin{array}{c} 1/\sqrt{T} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$
(6) Aus dem Tiefpass–Signal $s_{\rm TP0}(t)$ kann man auch das Bandpass–Signal $s_0(t)$ berechnen.
- Im Bereich $0 ≤ t ≤ T$ erhält man mit dem Ergebnis aus (5) das gleiche Ergebnis wie in der Teilaufgabe (1) :
- $$s_0(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\left[s_{{\rm TP}0}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \right] = {\rm Re}\left[\sqrt{E} /{\sqrt{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \right]= \sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$
- Daraus folgt: Die Energie $E$ bezieht sich auch bei Betrachtung im äquivalenten Tiefpass–Bereich auf das Bandpass–Signal.
- Entsprechend gilt für das mit blauem Punkt markierte Signal $s_2(t)$ im interessierenden Bereich:
- $$s_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\big[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \big] = {\rm Re}\big[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t)- \sqrt{E/T} \cdot \sin(2\pi f_{\rm T}t) \big] = - \sqrt{E/T} \cdot \sin(2\pi f_{\rm T}t) \hspace{0.05cm}.$$
- Schließlich kann für das (grüne) Signal $s_5(t)$ im Bereich $0 ≤ t < T$ geschrieben werden:
- $$s_5(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\big[\frac{-1 - {\rm j}}{\sqrt{2}} \cdot \sqrt{{E}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \big] = \text{...} = - \sqrt{\frac{E}{2T}} \cdot \cos(2\pi f_{\rm T}t)+ \sqrt{\frac{E}{2T}} \cdot \sin(2\pi f_{\rm T}t)=\sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t + 1.25 \cdot \pi) \hspace{0.05cm}.$$
- Auch diese Ergebnisse stimmen mit denen der Teilaufgaben (2) bzw. (3) überein. Zutreffend ist also der Lösungsvorschlag 2.