Aufgaben:Aufgabe 1.6Z: Ergodische Wahrscheinlichkeiten: Unterschied zwischen den Versionen
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Stochastische Signaltheorie/Markovketten}} | {{quiz-Header|Buchseite=Stochastische Signaltheorie/Markovketten}} | ||
| − | [[Datei:P_ID452__Sto_Z_1_6.png|right| | + | [[Datei:P_ID452__Sto_Z_1_6.png|right|frame|Markovkette mit $A$ und $B$]] |
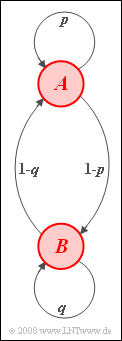
| − | Wir betrachten eine homogene stationäre Markovkette erster Ordnung mit den Ereignissen $A$ und $B$ und den Übergangswahrscheinlichkeiten entsprechend dem nebenstehenden Markovdiagramm: | + | Wir betrachten eine homogene stationäre Markovkette erster Ordnung mit den Ereignissen $A$ und $B$ und den Übergangswahrscheinlichkeiten entsprechend dem nebenstehenden Markovdiagramm: |
| − | Für die Teilaufgaben (1) bis (4) wird vorausgesetzt: | + | Für die Teilaufgaben '''(1)''' bis '''(4)''' wird vorausgesetzt: |
| − | *Nach dem Ereignis $A$ folgen $A$ und $B$ mit gleicher Wahrscheinlichkeit. | + | *Nach dem Ereignis $A$ folgen $A$ und $B$ mit gleicher Wahrscheinlichkeit. |
| − | *Nach $B$ ist das Ereignis $A$ doppelt so wahrscheinlich wie $B$. | + | *Nach $B$ ist das Ereignis $A$ doppelt so wahrscheinlich wie $B$. |
| − | Ab Teilaufgabe (5) sind $p$ und $q$ als freie Parameter zu verstehen, während die Ereigniswahrscheinlichkeiten ${\rm Pr}(A) = 2/3$ und ${\rm Pr}(B) = 1/3$ fest vorgegeben sind. | + | Ab Teilaufgabe '''(5)''' sind $p$ und $q$ als freie Parameter zu verstehen, während die Ereigniswahrscheinlichkeiten ${\rm Pr}(A) = 2/3$ und ${\rm Pr}(B) = 1/3$ fest vorgegeben sind. |
| − | + | ||
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Markovketten|Markovketten]]. | + | |
| − | + | ||
| − | *Sie können Ihre Ergebnisse mit dem | + | Hinweise: |
| − | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Markovketten|Markovketten]]. | |
| + | |||
| + | *Sie können Ihre Ergebnisse mit dem interaktiven Applet [[Applets:Markovketten|Ereigniswahrscheinlichkeiten einer Markovkette 1. Ordnung]] überprüfen. | ||
| Zeile 25: | Zeile 27: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß sind die Übergangswahrscheinlichkeiten $p$ und $q$? | + | {Wie groß sind die Übergangswahrscheinlichkeiten $p$ und $q$? |
|type="{}"} | |type="{}"} | ||
| − | $p \ = $ { 0.5 3% } | + | $p \ = \ $ { 0.5 3% } |
| − | $q \ = $ { 0.333 3% } | + | $q \ = \ $ { 0.333 3% } |
{Berechnen Sie die ergodischen Wahrscheinlichkeiten. | {Berechnen Sie die ergodischen Wahrscheinlichkeiten. | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(A) \ = $ { 0.571 3% } | + | ${\rm Pr}(A) \ = \ $ { 0.571 3% } |
| − | ${\rm Pr}(B) \ = $ { 0.429 3% } | + | ${\rm Pr}(B) \ = \ $ { 0.429 3% } |
| − | {Wie groß ist die bedingte Wahrscheinlichkeit, dass das Ereignis $B$ auftritt, wenn zwei Takte vorher das Ereignis $A$ aufgetreten ist? | + | {Wie groß ist die bedingte Wahrscheinlichkeit, dass das Ereignis $B$ auftritt, wenn zwei Takte vorher das Ereignis $A$ aufgetreten ist? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})\ = $ { 0.417 3% } | + | ${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})\ = \ $ { 0.417 3% } |
| − | {Wie groß ist die Rückschlusswahrscheinlichkeit, dass zwei Takte vorher das Ereignis $A$ aufgetreten ist, wenn aktuell $B$ auftritt? | + | {Wie groß ist die Rückschlusswahrscheinlichkeit, dass zwei Takte vorher das Ereignis $A$ aufgetreten ist, wenn aktuell $B$ auftritt? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(A_{\nu-2}\hspace{0.05cm}|\hspace{0.05cm}B_{\nu})\ = $ { 0.556 3% } | + | ${\rm Pr}(A_{\nu-2}\hspace{0.05cm}|\hspace{0.05cm}B_{\nu})\ = \ $ { 0.556 3% } |
| − | {Es gelte nun $p = 1/2$ und ${\rm Pr}(A) = 2/3$. Welcher Wert ergibt sich für $q$? | + | {Es gelte nun $p = 1/2$ und ${\rm Pr}(A) = 2/3$. Welcher Wert ergibt sich für $q$? |
|type="{}"} | |type="{}"} | ||
| − | $q\ = $ { 0. } | + | $q\ = \ $ { 0. } |
| − | {Wie | + | {Wie muss man die Parameter wählen, damit die Folgenelemente der Markovkette statistisch unabhängig sind und zusätzlich ${\rm Pr}(A) = 2/3$ gilt? |
|type="{}"} | |type="{}"} | ||
| − | $p \ = $ { 0.667 3% } | + | $p \ = \ $ { 0.667 3% } |
| − | $q \ = $ { 0.333 3% } | + | $q \ = \ $ { 0.333 3% } |
| Zeile 57: | Zeile 59: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Gemäß der Angabe gilt $p = 1 - p$ ⇒ $\underline{p =0.500}$ und $q = (1 - q)/2$, ⇒ $\underline{q =0.333}$. | |
| − | + | ||
| + | |||
| + | '''(2)''' Für die Ereigniswahrscheinlichkeit von $A$ gilt: | ||
:$${\rm Pr}(A) = \frac{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)}{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)+{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A)} = \frac{1-q}{1-q+1-p} = \frac{2/3}{2/3 + 1/2}= \frac{4}{7} \hspace{0.15cm}\underline {\approx0.571}.$$ | :$${\rm Pr}(A) = \frac{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)}{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)+{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A)} = \frac{1-q}{1-q+1-p} = \frac{2/3}{2/3 + 1/2}= \frac{4}{7} \hspace{0.15cm}\underline {\approx0.571}.$$ | ||
| − | + | *Damit ergibt sich ${\rm Pr}(B)= 1 - {\rm Pr}(A) = 3/7 \hspace{0.15cm}\underline {\approx 0.429}$. | |
| − | + | ||
| − | :$${\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.15cm} +\hspace{0.15cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) | + | |
| − | = | + | |
| − | + | '''(3)''' Über den Zeitpunkt $\nu-1$ ist keine Aussage getroffen. | |
| + | *Zu diesem Zeitpunkt kann $A$ oder $B$ aufgetreten sein. Deshalb gilt: | ||
| + | :$${\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.15cm} +\hspace{0.15cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) = p \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) + q \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) | ||
| + | = {5}/{12} \hspace{0.15cm}\underline {\approx 0.417}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' Nach dem Satz von Bayes gilt: | ||
:$${\rm Pr}(A_{\nu -2} \hspace{0.05cm} | \hspace{0.05cm}B_{\nu}) = \frac{{\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) \cdot {\rm Pr}(A_{\nu -2} ) }{{\rm Pr}(B_{\nu}) } = \frac{5/12 \cdot 4/7 }{3/7 } | :$${\rm Pr}(A_{\nu -2} \hspace{0.05cm} | \hspace{0.05cm}B_{\nu}) = \frac{{\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) \cdot {\rm Pr}(A_{\nu -2} ) }{{\rm Pr}(B_{\nu}) } = \frac{5/12 \cdot 4/7 }{3/7 } | ||
| − | = | + | = {5}/{9} \hspace{0.15cm}\underline {\approx 0.556}.$$ |
| − | :Die Wahrscheinlichkeit Pr( | + | ''Begründung:'' |
| − | + | *Die Wahrscheinlichkeit ${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})= 5/12$ wurde bereits im Unterpunkt '''(3)''' berechnet. | |
| + | *Aufgrund der Stationarität gilt ${\rm Pr}(A_{\nu-2})= {\rm Pr}(A) = 4/7$ und ${\rm Pr}(B_{\nu})= {\rm Pr}(B) = 3/7$. | ||
| + | *Damit erhält man für die gesuchte Rückschlusswahrscheinlichkeit nach obiger Gleichung den Wert $5/9$. | ||
| + | |||
| + | |||
| + | '''(5)''' Entsprechend der Teilaufgabe '''(2)''' gilt mit ${p =1/2}$ für die Wahrscheinlichkeit von $A$ allgemein: | ||
:$${\rm Pr}(A) = \frac{1-q}{1.5 -q}.$$ | :$${\rm Pr}(A) = \frac{1-q}{1.5 -q}.$$ | ||
| − | + | *Aus $ {\rm Pr}(A) = 2/3$ folgt somit $\underline{q =0}$. | |
| − | + | ||
| + | |||
| + | |||
| + | '''(6)''' Im Fall der statistischen Unabhängigkeit muss beispielsweise gelten: | ||
:$${{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A)} = {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)} = {{\rm Pr}(A)}.$$ | :$${{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A)} = {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)} = {{\rm Pr}(A)}.$$ | ||
| − | + | *Daraus folgt $p = {\rm Pr}(A) \hspace{0.15cm}\underline {= 2/3}$ und dementsprechend $q = 1-p \hspace{0.15cm}\underline {= 1/3}$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 2. Dezember 2021, 15:21 Uhr
Wir betrachten eine homogene stationäre Markovkette erster Ordnung mit den Ereignissen $A$ und $B$ und den Übergangswahrscheinlichkeiten entsprechend dem nebenstehenden Markovdiagramm:
Für die Teilaufgaben (1) bis (4) wird vorausgesetzt:
- Nach dem Ereignis $A$ folgen $A$ und $B$ mit gleicher Wahrscheinlichkeit.
- Nach $B$ ist das Ereignis $A$ doppelt so wahrscheinlich wie $B$.
Ab Teilaufgabe (5) sind $p$ und $q$ als freie Parameter zu verstehen, während die Ereigniswahrscheinlichkeiten ${\rm Pr}(A) = 2/3$ und ${\rm Pr}(B) = 1/3$ fest vorgegeben sind.
Hinweise:
- Die Aufgabe gehört zum Kapitel Markovketten.
- Sie können Ihre Ergebnisse mit dem interaktiven Applet Ereigniswahrscheinlichkeiten einer Markovkette 1. Ordnung überprüfen.
Fragebogen
Musterlösung
(2) Für die Ereigniswahrscheinlichkeit von $A$ gilt:
- $${\rm Pr}(A) = \frac{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)}{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)+{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A)} = \frac{1-q}{1-q+1-p} = \frac{2/3}{2/3 + 1/2}= \frac{4}{7} \hspace{0.15cm}\underline {\approx0.571}.$$
- Damit ergibt sich ${\rm Pr}(B)= 1 - {\rm Pr}(A) = 3/7 \hspace{0.15cm}\underline {\approx 0.429}$.
(3) Über den Zeitpunkt $\nu-1$ ist keine Aussage getroffen.
- Zu diesem Zeitpunkt kann $A$ oder $B$ aufgetreten sein. Deshalb gilt:
- $${\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.15cm} +\hspace{0.15cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) = p \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) + q \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) = {5}/{12} \hspace{0.15cm}\underline {\approx 0.417}.$$
(4) Nach dem Satz von Bayes gilt:
- $${\rm Pr}(A_{\nu -2} \hspace{0.05cm} | \hspace{0.05cm}B_{\nu}) = \frac{{\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) \cdot {\rm Pr}(A_{\nu -2} ) }{{\rm Pr}(B_{\nu}) } = \frac{5/12 \cdot 4/7 }{3/7 } = {5}/{9} \hspace{0.15cm}\underline {\approx 0.556}.$$
Begründung:
- Die Wahrscheinlichkeit ${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})= 5/12$ wurde bereits im Unterpunkt (3) berechnet.
- Aufgrund der Stationarität gilt ${\rm Pr}(A_{\nu-2})= {\rm Pr}(A) = 4/7$ und ${\rm Pr}(B_{\nu})= {\rm Pr}(B) = 3/7$.
- Damit erhält man für die gesuchte Rückschlusswahrscheinlichkeit nach obiger Gleichung den Wert $5/9$.
(5) Entsprechend der Teilaufgabe (2) gilt mit ${p =1/2}$ für die Wahrscheinlichkeit von $A$ allgemein:
- $${\rm Pr}(A) = \frac{1-q}{1.5 -q}.$$
- Aus $ {\rm Pr}(A) = 2/3$ folgt somit $\underline{q =0}$.
(6) Im Fall der statistischen Unabhängigkeit muss beispielsweise gelten:
- $${{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A)} = {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)} = {{\rm Pr}(A)}.$$
- Daraus folgt $p = {\rm Pr}(A) \hspace{0.15cm}\underline {= 2/3}$ und dementsprechend $q = 1-p \hspace{0.15cm}\underline {= 1/3}$.