Aufgaben:Aufgabe 1.7Z: Systemanalyse

• Zurück zum Buch

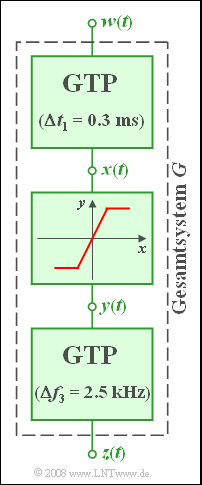
Ein Gesamtsystem $G$ mit Eingang $w(t)$ und Ausgang $z(t)$ besteht aus drei Komponenten:

• Die erste Komponente ist ein Gaußtiefpass mit Impulsantwort

$$h_1(t) = \frac{1}{\Delta t_1} \cdot {\rm e}^{-\pi(t/\Delta t_1)^2}, \hspace{0.5cm} \Delta t_1= {0.3\,\rm ms}.$$

• Danach folgt eine Nichtlinearität mit Kennlinie

$$y(t) = \left\{ \begin{array}{c} {8\,\rm V} \\ 2 \cdot x(t) \\ {-8\,\rm V} \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {x(t) \ge {4\,\rm V}}, \\ {{-4\,\rm V} < x(t) < {4\,\rm V}}, \\ {x(t)\le {-4\,\rm V}}. \\ \end{array}$$

Deren Eingangssignal $x(t)$ wird um den Faktor 2 verstärkt und – falls nötig – auf den Amplitudenbereich ±8V begrenzt.

• Am Ende der Kette folgt wieder ein Gaußtiefpass, der durch seinen Frequenzgang gegeben ist:

$$H_3(f) = {\rm e}^{-\pi(f/\Delta f_3)^2}, \hspace{0.5cm} \Delta f_3= {2.5\,\rm kHz}.$$

Das Eingangssignal $w(t)$ sei ein Gaußimpuls mit konstanter Amplitude 5 V, aber variabler Breite $T$: $$w(t) = {5\,\rm V}\cdot {\rm e}^{-\pi(t/T)^2}.$$ Zu untersuchen ist, in welchem Bereich die äquivalente Impulsdauer $T$ dieses Gaußimpulses variieren kann, damit das Gesamtsystem durch den Frequenzband $$H_{\rm G}(f) = K \cdot {\rm e}^{-\pi(f/\Delta f_{\rm G})^2}$$ vollständig beschrieben wird. Der Index „G” bei Frequenzgang und Bandbreite bezieht sich jeweils auf „Gesamtsystem”.

Hinweis: Die Aufgabe bezieht sich auf den Abschnitt Gaußtiefpass im Kapitel 1.3.

Fragebogen

1

Welche Bedingungen müssen erfüllt sein, damit das Gesamtsystem durch einen einzigen Frequenzgang beschreibbar ist?

	Es besteht ein linearer Zusammenhang zwischen $w(t)$ und $z(t)$.
	$H_3(f)$ muss schmalbandiger sein als $H_1(f)$.
	Das Signal $x(t)$ darf betragsmäßig nicht größer sein als 4 V.

2

Berechnen Sie den Maximalwert für die äquivalente Impulsdauer $T$, damit die unter a) genannten Bedingungen erfüllbar sind.

$T_{\rm max} =$ ms

3

Geben Sie die Parameter des Gesamtfrequenzgangs $H_{\rm G}(f)$ an.

$K =$

$\Delta f_{\rm G} =$ kHz

Musterlösung

Musterlösung

a)

b)

c)

d)

e)

f)

g)