Modulationsverfahren/Einseitenbandmodulation: Unterschied zwischen den Versionen
| Zeile 46: | Zeile 46: | ||
*Bei ZSB–AM wird mit dem empfangsseitigen Trägersignal $z_{\rm E}(t) = 2 · \cos(ω_{\rm T} · t)$ erreicht, dass $υ(t) = q(t)$ gilt. Dagegen muss bei ESB–AM die Trägeramplitude auf 4 erhöht werden. | *Bei ZSB–AM wird mit dem empfangsseitigen Trägersignal $z_{\rm E}(t) = 2 · \cos(ω_{\rm T} · t)$ erreicht, dass $υ(t) = q(t)$ gilt. Dagegen muss bei ESB–AM die Trägeramplitude auf 4 erhöht werden. | ||
| + | ==Einfluss eines Frequenz– und Phasenversatzes== | ||
| + | Besteht ein Frequenzversatz zwischen den Trägersignalen $z(t)$ und $z_{\rm E}(t)$, so kommt es stets zu starken nichtlinearen Verzerrungen, also unabhängig davon, ob ZSB–AM oder ESB–AM vorliegt. Bei der Realisierung eines Synchrondemodulators ist deshalb eine perfekte Frequenzsynchronisation unerlässlich. | ||
| + | Betrachten wir nun den Einfluss eines Phasenversatzes $Δ{\mathbf ϕ}_{\rm T}$ zwischen sende– und empfangsseitigem Trägersignal, und zwar am Beispiel des Quellensignals | ||
| + | $$q(t) = A_1 \cdot \cos(\omega_1 \cdot t ) + A_2 \cdot \cos(\omega_2 \cdot t)\hspace{0.05cm}.$$ | ||
| + | Bei ZSB–AM führt ein solcher Phasenversatz lediglich zu einer frequenzunabhängigen Dämpfung, aber nicht zu Verzerrungen: | ||
| + | $$v(t) = \cos (\Delta \phi_{\rm T}) \cdot q(t) = \cos (\Delta \phi_{\rm T}) \cdot A_1 \cdot \cos(\omega_1 \cdot t ) + \cos (\Delta \phi_{\rm T}) \cdot A_2 \cdot \cos(\omega_2 \cdot t ) \hspace{0.05cm}.$$ | ||
| + | Dagegen erhält man bei der OSB–AM: | ||
| + | $$\begin{align*}v(t) & = A_1 \cdot \cos(\omega_1 \cdot t - \Delta \phi_{\rm T}) + A_2 | ||
| + | \cdot \cos(\omega_2 \cdot t - \Delta \phi_{\rm T})=\\ | ||
| + | & = A_1 \cdot \cos(\omega_1 \cdot (t - \tau_1)) + A_2 \cdot | ||
| + | \cos(\omega_2 \cdot (t - \tau_2))\hspace{0.05cm}.\end{align*}$$ | ||
| + | |||
| + | Man erkennt aus dieser Gleichung: | ||
| + | *Die beiden Laufzeiten $τ_1 = Δ{\mathbf ϕ}_{\rm T}/ω_1$ und $τ_2 = Δ{\mathbf ϕ}_{\rm T}/ω_2$ sind unterschiedlich. Das bedeutet, dass ein Phasenversatz bei ESB–AM (OSB–AM oder USB–AM) zu Phasenverzerrungen führt. | ||
| + | *Ein positiver Wert von $Δ{\mathbf ϕ}_{\rm T}$ bewirkt bei OSB positive Werte von $τ_1$ und $τ_2$ (also gegenüber dem Cosinus nachlaufende Signale) und bei USB negative $τ_1$– bzw. $τ_2$–Werte (vorlaufende Signale). | ||
| + | |||
| + | |||
| + | Die Auswirkungen von Phasenverzerrungen auf ein aus zwei Cosinusschwingungen zusammengesetztes Nachrichtensignal können Sie sich mit folgendem Interaktionsmodul verdeutlichen: | ||
| + | |||
| + | Lineare Verzerrungen periodischer Signale | ||
Version vom 18. Juni 2016, 18:42 Uhr
Beschreibung im Frequenzbereich
Die ZSB–AM – sowohl mit als auch ohne Träger – hat folgende Eigenschaften:
- Das modulierte Signal $s(t)$ benötigt die doppelte Bandbreite wie das Quellensignal $q(t)$.
- Die vollständige Information über $q(t)$ steckt sowohl im oberen als auch im unteren Seitenband.
Die so genannte Einseitenband–Amplitudenmodulation (ESB–AM) macht sich diese Eigenschaft dadurch zunutze, dass nur eines dieser Seitenbänder übertragen wird, entweder das obere Seitenband (OSB) oder das untere Seitenband (USB).
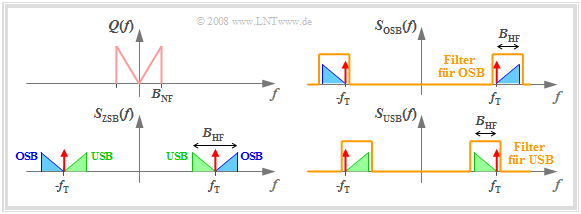
Die Grafik verdeutlicht die ESB–AM im Frequenzbereich und gibt gleichzeitig eine Realisierungsform des ESB–Modulators an. Man erkennt aus dieser Darstellung:
- Das ESB–Spektrum ergibt sich aus dem ZSB–Spektrum durch Filterung mit einem Bandpass, der bezüglich der Trägerfrequenz $f_{\rm T}$ ein unsymmetrisches Verhalten zeigt.
- Bei OSB–Modulation wird die untere Grenzfrequenz $f_{\rm U} = f_{\rm T} – f_ε$ und die obere Grenzfrequenz zu $f_{\rm O} ≥ f_{\rm T} + B_{\rm NF}$ gewählt $(f_ε$ ist eine beliebig kleine positive Frequenz). Das OSB–Spektrum beinhaltet somit nur das obere Seitenband und (nicht notwendigerweise) den Träger.
- Zur Erzeugung einer USB–Modulation müssen dagegen die untere bzw. obere Grenzfrequenz des Bandpasses wie folgt festgelegt werden: $f_{\rm U} ≤ f_{\rm T} – B_{\rm NF}, f_{\rm O} = f_{\rm T} + f_ε.$
Bei $f_{\rm T} =$ 100 kHz und $B_{\rm NF} =$ 3 kHz erhält man aus dem ZSB–Signal ein OSB–Signal mit Träger, wenn das Filter alle Frequenzen unterhalb von 99.999... kHz abschneidet.
- Ist die untere Grenzfrequenz um ein (beliebig kleines) „epsilon” größer als $f_{\rm T}$, so ergibt sich eine „OSB–AM ohne Träger”.
- Eine „USB mit/ohne Träger” kann entsprechend mit $f_{\rm O} =$ 100 kHz bzw. $f_{\rm O} =$ 99.999... kHz realisiert werden.
Der große Vorteil einer ESB–AM liegt in der nur halben Bandbreite gegenüber der ZSB–AM. Mit welchen Nachteilen dieser Vorteil erkauft werden muss, wird in den nachfolgenden Abschnitten erläutert.
Synchrondemodulation eines ESB–Signals
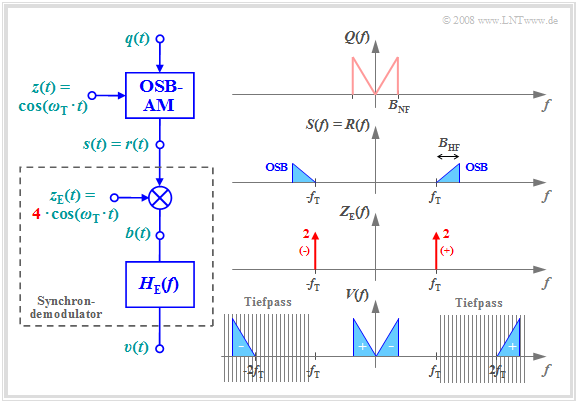
Wir betrachten nun ein ESB–moduliertes Signal und beim Empfänger den in Kapitel 2.2 beschriebenen Synchrondemodulator, wobei perfekte Frequenz– und Phasensynchronisation vorausgesetzt wird. Ohne Einfluss auf die Allgemeingültigkeit ist im weiteren Verlauf dieses Abschnitts stets ${\mathbf ϕ}_{\rm T} =$ 0 gesetzt.
Ein Vergleich mit den Eigenschaften des Synchrondemodulators bei ZSB–AM in Kapitel 2.2 zeigt folgende Gemeinsamkeiten und Unterschiede:
- Das Spektrum $V(f)$ des Sinkensignals ergibt sich in beiden Fällen aus der Faltung der Spektren $R(f)$ und $Z_{\rm E}(f)$, wobei Letzteres sich aus zwei Diracfunktionen bei $±f_{\rm T}$ zusammensetzt.
- Bei ZSB–AM überlagern sich für jede Frequenz die Faltungsprodukte mit der rechten und der linken Diracfunktion. In der Grafik zu Kapitel 2.2 sind diese Anteile mit „+” bzw. „–” markiert.
- Dagegen liefert bei OSB–Modulation nur die Faltung mit der Diraclinie bei $\ –f_{\rm T}$ den $V(f)$–Anteil bei positiven Frequenzen und bei USB–Modulation die Faltung mit der Diracfunktion $δ(f – f_{\rm T})$.
- Bei ZSB–AM wird mit dem empfangsseitigen Trägersignal $z_{\rm E}(t) = 2 · \cos(ω_{\rm T} · t)$ erreicht, dass $υ(t) = q(t)$ gilt. Dagegen muss bei ESB–AM die Trägeramplitude auf 4 erhöht werden.
Einfluss eines Frequenz– und Phasenversatzes
Besteht ein Frequenzversatz zwischen den Trägersignalen $z(t)$ und $z_{\rm E}(t)$, so kommt es stets zu starken nichtlinearen Verzerrungen, also unabhängig davon, ob ZSB–AM oder ESB–AM vorliegt. Bei der Realisierung eines Synchrondemodulators ist deshalb eine perfekte Frequenzsynchronisation unerlässlich.
Betrachten wir nun den Einfluss eines Phasenversatzes $Δ{\mathbf ϕ}_{\rm T}$ zwischen sende– und empfangsseitigem Trägersignal, und zwar am Beispiel des Quellensignals $$q(t) = A_1 \cdot \cos(\omega_1 \cdot t ) + A_2 \cdot \cos(\omega_2 \cdot t)\hspace{0.05cm}.$$ Bei ZSB–AM führt ein solcher Phasenversatz lediglich zu einer frequenzunabhängigen Dämpfung, aber nicht zu Verzerrungen: $$v(t) = \cos (\Delta \phi_{\rm T}) \cdot q(t) = \cos (\Delta \phi_{\rm T}) \cdot A_1 \cdot \cos(\omega_1 \cdot t ) + \cos (\Delta \phi_{\rm T}) \cdot A_2 \cdot \cos(\omega_2 \cdot t ) \hspace{0.05cm}.$$ Dagegen erhält man bei der OSB–AM: $$\begin{align*}v(t) & = A_1 \cdot \cos(\omega_1 \cdot t - \Delta \phi_{\rm T}) + A_2 \cdot \cos(\omega_2 \cdot t - \Delta \phi_{\rm T})=\\ & = A_1 \cdot \cos(\omega_1 \cdot (t - \tau_1)) + A_2 \cdot \cos(\omega_2 \cdot (t - \tau_2))\hspace{0.05cm}.\end{align*}$$
Man erkennt aus dieser Gleichung:
- Die beiden Laufzeiten $τ_1 = Δ{\mathbf ϕ}_{\rm T}/ω_1$ und $τ_2 = Δ{\mathbf ϕ}_{\rm T}/ω_2$ sind unterschiedlich. Das bedeutet, dass ein Phasenversatz bei ESB–AM (OSB–AM oder USB–AM) zu Phasenverzerrungen führt.
- Ein positiver Wert von $Δ{\mathbf ϕ}_{\rm T}$ bewirkt bei OSB positive Werte von $τ_1$ und $τ_2$ (also gegenüber dem Cosinus nachlaufende Signale) und bei USB negative $τ_1$– bzw. $τ_2$–Werte (vorlaufende Signale).
Die Auswirkungen von Phasenverzerrungen auf ein aus zwei Cosinusschwingungen zusammengesetztes Nachrichtensignal können Sie sich mit folgendem Interaktionsmodul verdeutlichen:
Lineare Verzerrungen periodischer Signale