Aufgaben:Aufgabe 4.4: Maximum–a–posteriori und Maximum–Likelihood: Unterschied zwischen den Versionen
| (16 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Struktur des optimalen Empfängers}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Struktur des optimalen Empfängers}} | ||
| + | |||
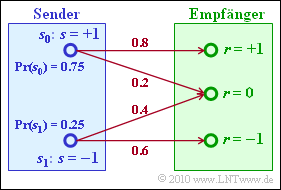
| + | [[Datei:P_ID2013__Dig_A_4_4.png|right|frame|Kanalübergangswahrscheinlichkeiten]] | ||
| + | Zur Verdeutlichung von "Maximum–a–posteriori" $\rm (MAP)$– und "Maximum–Likelihood" $\rm (ML)$–Entscheidung konstruieren wir nun ein sehr einfaches Beispiel mit nur zwei möglichen Nachrichten $m_0 = 0$ und $m_1 = 1$, die durch die Signalwerte $s_0$ bzw. $s_1$ dargestellt werden: | ||
| + | :$$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_0 = +1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_0 = 0\hspace{0.05cm},$$ | ||
| + | :$$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_1 = -1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_1 = 1\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Die Auftrittswahrscheinlichkeiten seien: | ||
| + | :$${\rm Pr}(s = s_0) = 0.75,\hspace{0.2cm}{\rm Pr}(s = s_1) = 0.25 \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Das Empfangssignal kann – warum auch immer – drei verschiedene Werte annehmen, nämlich | ||
| + | :$$r = +1,\hspace{0.2cm}r = 0,\hspace{0.2cm}r = -1 \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Die bedingten Kanalwahrscheinlichkeiten können der Grafik entnommen werden. | ||
| + | |||
| + | |||
| + | Nach der Übertragung soll die gesendete Nachricht durch einen optimalen Empfänger geschätzt werden. Zur Verfügung stehen: | ||
| + | * der '''Maximum–Likelihood–Empfänger''' $\rm (ML$–Empfänger$)$, der die Auftrittswahrscheinlichkeiten ${\rm Pr}(s = s_i)$ nicht kennt, mit der Entscheidungsregel: | ||
| + | :$$\hat{m}_{\rm ML} = {\rm arg} \max_i \hspace{0.1cm} \big[ p_{r |s } \hspace{0.05cm} (\rho | ||
| + | |s_i ) \big]\hspace{0.05cm},$$ | ||
| + | |||
| + | * der '''Maximum–a–posteriori–Empfänger''' $\rm (MAP$–Empfänger$)$; dieser berücksichtigt bei seiner Entscheidung auch die Symbolwahrscheinlichkeiten der Quelle: | ||
| + | :$$\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big[ {\rm Pr}( s = s_i) \cdot p_{r |s } \hspace{0.05cm} (\rho | ||
| + | |s_i ) \big ]\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Optimale_Empf%C3%A4ngerstrategien| "Optimale Empfängerstrategien"]]. | ||
| + | |||
| + | *Bezug genommen wird auch auf das Kapitel [[Digitalsignal%C3%BCbertragung/Struktur_des_optimalen_Empf%C3%A4ngers| "Struktur des optimalen Empfängers"]]. | ||
| + | |||
| + | * Die notwendigen statistischen Grundlagen finden Sie im Kapitel [[Stochastische_Signaltheorie/Statistische_Abh%C3%A4ngigkeit_und_Unabh%C3%A4ngigkeit| "Statistische Abhängigkeit und Unabhängigkeit"]] des Buches „Stochastische Signaltheorie”. | ||
| + | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| + | <quiz display=simple> | ||
| + | {Mit welchen Wahrscheinlichkeiten treten die Empfangswerte auf? | ||
| + | |type="{}"} | ||
| + | ${\rm Pr}(r = +1) \ = \ $ { 0.6 3% } | ||
| + | ${\rm Pr}(r = -1) \ = \ $ { 0.15 3% } | ||
| + | ${\rm Pr}(r = 0) \hspace{0.45cm} = \ $ { 0.25 3% } | ||
| − | + | {Berechnen Sie alle Rückschlusswahrscheinlichkeiten. | |
| − | { | + | |type="{}"} |
| − | |type=" | + | ${\rm Pr}(s_0|r = +1) \ = \ $ { 1 3% } |
| − | - | + | ${\rm Pr}(s_1|r = +1) \ = \ $ { 0. } |
| − | + | ${\rm Pr}(s_0|r = -1) \ = \ $ { 0. } | |
| + | ${\rm Pr}(s_1|r = -1) \ = \ $ { 1 3% } | ||
| + | ${\rm Pr}(s_0|r = 0) \hspace{0.45cm} = \ $ { 0.6 3% } | ||
| + | ${\rm Pr}(s_1|r = 0) \hspace{0.45cm} = \ $ { 0.4 3% } | ||
| + | {Unterscheiden sich MAP– und ML–Empfänger unter der Voraussetzung „$r = +1$”? | ||
| + | |type="()"} | ||
| + | - ja, | ||
| + | + nein. | ||
| − | { | + | {Unterscheiden sich MAP– und ML–Empfänger unter der Voraussetzung „$r = -1$”? |
| − | |type=" | + | |type="()"} |
| − | + | - ja, | |
| + | + nein. | ||
| + | {Welche Aussagen gelten unter der Voraussetzung „$r = 0$”? | ||
| + | |type="[]"} | ||
| + | + Der MAP–Empfänger entscheidet sich für $s_0$. | ||
| + | - Der MAP–Empfänger entscheidet sich für $s_1$. | ||
| + | - Der ML–Empfänger entscheidet sich für $s_0$. | ||
| + | + Der ML–Empfänger entscheidet sich für $s_1$. | ||
| + | {Berechnen Sie die Symbolfehlerwahrscheinlichkeit des '''ML–Empfängers'''. | ||
| + | |type="{}"} | ||
| + | ${\rm Pr(Symbolfehler)}\ = \ $ { 0.15 3% } | ||
| + | {Berechnen Sie die Symbolfehlerwahrscheinlichkeit des '''MAP–Empfängers'''. | ||
| + | |type="{}"} | ||
| + | ${\rm Pr(Symbolfehler)}\ = \ $ { 0.1 3% } | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Die gesuchten empfängerseitigen Auftrittswahrscheinlichkeiten sind |
| − | '''(2)''' | + | :$${\rm Pr} ( r = +1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} ( s_0) \cdot {\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s = +1) = 0.75 \cdot 0.8 \hspace{0.05cm}\hspace{0.15cm}\underline { = 0.6}\hspace{0.05cm},$$ |
| − | '''(3)''' | + | :$${\rm Pr} ( r = -1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} ( s_1) \cdot {\rm Pr} ( r = -1 \hspace{0.05cm}| \hspace{0.05cm}s = -1) = 0.25 \cdot 0.6 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.15}\hspace{0.05cm},$$ |
| − | '''(4)''' | + | :$${\rm Pr} ( r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 - {\rm Pr} ( r = +1) - {\rm Pr} ( r = -1) = 1 - 0.6 - 0.15 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm}.$$ |
| − | '''(5)''' | + | |
| − | '''(6)''' | + | *Für die letzte Wahrscheinlichkeit gilt auch: |
| + | :$${\rm Pr} ( r = 0) = 0.75 \cdot 0.2 + 0.25 \cdot 0.4 = 0.25\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' Für die erste gesuchte Rückschlusswahrscheinlichkeit gilt: | ||
| + | :$${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) = \frac{{\rm Pr} ( r = +1 \hspace{0.05cm}|\hspace{0.05cm}s_0 ) \cdot {\rm Pr} ( s_0)}{{\rm Pr} ( r = +1)} | ||
| + | = \frac{0.8 \cdot 0.75}{0.6} \hspace{0.05cm}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Entsprechend erhält man für die weiteren Wahrscheinlichkeiten: | ||
| + | :$${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{-0.1cm} \ = \ 1 - {\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$ | ||
| + | :$${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = -1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$ | ||
| + | :$${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = -1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm},$$ | ||
| + | :$${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{{\rm Pr} ( r = 0 \hspace{0.05cm}|\hspace{0.05cm}s_0 ) \cdot {\rm Pr} ( s_0)}{{\rm Pr} ( r = 0 )}= \frac{0.2 \cdot 0.75}{0.25} \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.6}\hspace{0.05cm},$$ | ||
| + | :$${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1- {\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.4} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Es gelte $r = +1$. Dann entscheidet sich | ||
| + | * der MAP–Empfänger für $s_0$, da ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) = 1 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1)= 0\hspace{0.05cm},$ | ||
| + | |||
| + | * der ML–Empfänger ebenfalls für $s_0$, da ${\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.8 > {\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0 \hspace{0.05cm}.$ | ||
| + | |||
| + | |||
| + | Richtig ist also <u>NEIN</u>. | ||
| + | |||
| + | |||
| + | '''(4)''' <u>NEIN</u> gilt auch unter der Voraussetzung „$r = \, –1$”, da keine Verbindung zwischen $s_0$ und „$r = \, –1$” besteht. | ||
| + | |||
| + | |||
| + | '''(5)''' Richtig sind die <u>Lösungsvorschläge 1 und 4</u>: | ||
| + | *Der MAP–Empfänger entscheidet sich für das Ereignis $s_0$, da ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.6 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.4 \hspace{0.05cm}.$ | ||
| + | *Dagegen wird sich der ML–Empfänger für $s_1$ entscheiden, da ${\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0.4 > {\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.2 \hspace{0.05cm}.$ | ||
| + | |||
| + | |||
| + | '''(6)''' Der Maximum–Likelihood–Empfänger | ||
| + | * entscheidet sich nur für $s_0$, wenn $r = +1$ ist, | ||
| + | |||
| + | * macht also keinen Fehler, wenn $s_1$ gesendet wurde, | ||
| + | |||
| + | * macht nur einen Fehler bei der Kombination „$s_0$” und „$r = 0$”: | ||
| + | :$${\rm Pr} ({\rm Symbolfehler} ) = {\rm Pr} ({\cal E } ) = 0.75 \cdot 0.2 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.15} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(7)''' Der MAP–Empfänger entscheidet sich dagegen bei „$r = 0$” für $s_0$. | ||
| + | * Einen Symbolfehler gibt es also nur in der Kombination „$s_1$” und „$r = 0$”. Daraus folgt: | ||
| + | :$${\rm Pr} ({\rm Symbolfehler} ) = {\rm Pr} ({\cal E } ) = 0.25 \cdot 0.4 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.1} \hspace{0.05cm}.$$ | ||
| + | *Die Fehlerwahrscheinlichkeit ist hier geringer als beim ML–Empfänger, | ||
| + | *da nun auch die unterschiedlichen A-priori–Wahrscheinlichkeiten ${\rm Pr}(s_0)$ und ${\rm Pr}(s_1)$ berücksichtigt werden. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 15. Juli 2022, 16:22 Uhr
Zur Verdeutlichung von "Maximum–a–posteriori" $\rm (MAP)$– und "Maximum–Likelihood" $\rm (ML)$–Entscheidung konstruieren wir nun ein sehr einfaches Beispiel mit nur zwei möglichen Nachrichten $m_0 = 0$ und $m_1 = 1$, die durch die Signalwerte $s_0$ bzw. $s_1$ dargestellt werden:
- $$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_0 = +1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_0 = 0\hspace{0.05cm},$$
- $$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_1 = -1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_1 = 1\hspace{0.05cm}.$$
- Die Auftrittswahrscheinlichkeiten seien:
- $${\rm Pr}(s = s_0) = 0.75,\hspace{0.2cm}{\rm Pr}(s = s_1) = 0.25 \hspace{0.05cm}.$$
- Das Empfangssignal kann – warum auch immer – drei verschiedene Werte annehmen, nämlich
- $$r = +1,\hspace{0.2cm}r = 0,\hspace{0.2cm}r = -1 \hspace{0.05cm}.$$
- Die bedingten Kanalwahrscheinlichkeiten können der Grafik entnommen werden.
Nach der Übertragung soll die gesendete Nachricht durch einen optimalen Empfänger geschätzt werden. Zur Verfügung stehen:
- der Maximum–Likelihood–Empfänger $\rm (ML$–Empfänger$)$, der die Auftrittswahrscheinlichkeiten ${\rm Pr}(s = s_i)$ nicht kennt, mit der Entscheidungsregel:
- $$\hat{m}_{\rm ML} = {\rm arg} \max_i \hspace{0.1cm} \big[ p_{r |s } \hspace{0.05cm} (\rho |s_i ) \big]\hspace{0.05cm},$$
- der Maximum–a–posteriori–Empfänger $\rm (MAP$–Empfänger$)$; dieser berücksichtigt bei seiner Entscheidung auch die Symbolwahrscheinlichkeiten der Quelle:
- $$\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big[ {\rm Pr}( s = s_i) \cdot p_{r |s } \hspace{0.05cm} (\rho |s_i ) \big ]\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel "Optimale Empfängerstrategien".
- Bezug genommen wird auch auf das Kapitel "Struktur des optimalen Empfängers".
- Die notwendigen statistischen Grundlagen finden Sie im Kapitel "Statistische Abhängigkeit und Unabhängigkeit" des Buches „Stochastische Signaltheorie”.
Fragebogen
Musterlösung
- $${\rm Pr} ( r = +1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} ( s_0) \cdot {\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s = +1) = 0.75 \cdot 0.8 \hspace{0.05cm}\hspace{0.15cm}\underline { = 0.6}\hspace{0.05cm},$$
- $${\rm Pr} ( r = -1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} ( s_1) \cdot {\rm Pr} ( r = -1 \hspace{0.05cm}| \hspace{0.05cm}s = -1) = 0.25 \cdot 0.6 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.15}\hspace{0.05cm},$$
- $${\rm Pr} ( r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 - {\rm Pr} ( r = +1) - {\rm Pr} ( r = -1) = 1 - 0.6 - 0.15 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm}.$$
- Für die letzte Wahrscheinlichkeit gilt auch:
- $${\rm Pr} ( r = 0) = 0.75 \cdot 0.2 + 0.25 \cdot 0.4 = 0.25\hspace{0.05cm}.$$
(2) Für die erste gesuchte Rückschlusswahrscheinlichkeit gilt:
- $${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) = \frac{{\rm Pr} ( r = +1 \hspace{0.05cm}|\hspace{0.05cm}s_0 ) \cdot {\rm Pr} ( s_0)}{{\rm Pr} ( r = +1)} = \frac{0.8 \cdot 0.75}{0.6} \hspace{0.05cm}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$
- Entsprechend erhält man für die weiteren Wahrscheinlichkeiten:
- $${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{-0.1cm} \ = \ 1 - {\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$
- $${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = -1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$
- $${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = -1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm},$$
- $${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{{\rm Pr} ( r = 0 \hspace{0.05cm}|\hspace{0.05cm}s_0 ) \cdot {\rm Pr} ( s_0)}{{\rm Pr} ( r = 0 )}= \frac{0.2 \cdot 0.75}{0.25} \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.6}\hspace{0.05cm},$$
- $${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1- {\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.4} \hspace{0.05cm}.$$
(3) Es gelte $r = +1$. Dann entscheidet sich
- der MAP–Empfänger für $s_0$, da ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) = 1 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1)= 0\hspace{0.05cm},$
- der ML–Empfänger ebenfalls für $s_0$, da ${\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.8 > {\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0 \hspace{0.05cm}.$
Richtig ist also NEIN.
(4) NEIN gilt auch unter der Voraussetzung „$r = \, –1$”, da keine Verbindung zwischen $s_0$ und „$r = \, –1$” besteht.
(5) Richtig sind die Lösungsvorschläge 1 und 4:
- Der MAP–Empfänger entscheidet sich für das Ereignis $s_0$, da ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.6 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.4 \hspace{0.05cm}.$
- Dagegen wird sich der ML–Empfänger für $s_1$ entscheiden, da ${\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0.4 > {\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.2 \hspace{0.05cm}.$
(6) Der Maximum–Likelihood–Empfänger
- entscheidet sich nur für $s_0$, wenn $r = +1$ ist,
- macht also keinen Fehler, wenn $s_1$ gesendet wurde,
- macht nur einen Fehler bei der Kombination „$s_0$” und „$r = 0$”:
- $${\rm Pr} ({\rm Symbolfehler} ) = {\rm Pr} ({\cal E } ) = 0.75 \cdot 0.2 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.15} \hspace{0.05cm}.$$
(7) Der MAP–Empfänger entscheidet sich dagegen bei „$r = 0$” für $s_0$.
- Einen Symbolfehler gibt es also nur in der Kombination „$s_1$” und „$r = 0$”. Daraus folgt:
- $${\rm Pr} ({\rm Symbolfehler} ) = {\rm Pr} ({\cal E } ) = 0.25 \cdot 0.4 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.1} \hspace{0.05cm}.$$
- Die Fehlerwahrscheinlichkeit ist hier geringer als beim ML–Empfänger,
- da nun auch die unterschiedlichen A-priori–Wahrscheinlichkeiten ${\rm Pr}(s_0)$ und ${\rm Pr}(s_1)$ berücksichtigt werden.