Aufgaben:Aufgabe 3.12: Trellisdiagramm für zwei Vorläufer: Unterschied zwischen den Versionen
Aus LNTwww
| (16 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Viterbi–Empfänger}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Viterbi–Empfänger}} | ||
| − | [[Datei:P_ID1478__Dig_A_3_12.png|right|frame|Trellisdiagramm für | + | [[Datei:P_ID1478__Dig_A_3_12.png|right|frame|Trellisdiagramm für zwei Vorläufer]] |
| − | Wir gehen von den Grundimpulswerten $g_0$, $g_{\rm –1}$ | + | Wir gehen von den Grundimpulswerten $g_0\ne 0$, $g_{\rm –1}\ne 0$ and $g_{\rm –2}\ne 0$ aus: |
| − | :$${\it \Gamma}_{\nu-1}(00) + \varepsilon_{\nu}(001) \hspace{0.15cm}{\rm und} | + | *Das bedeutet, dass die Entscheidung über das Symbol $a_{\rm \nu}$ auch durch die nachfolgenden Koeffizienten $a_{\rm \nu +1}$ und $a_{\rm \nu +2}$ beeinflusst wird. |
| − | \hspace{0.15cm}{\it \Gamma}_{\nu-1}(10) + \varepsilon_{\nu}(101).$$ | + | |
| + | *Damit sind für jeden Zeitpunkt $\nu$ genau acht Fehlergrößen $\varepsilon_{\rm \nu}$ zu bestimmen, aus denen die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(00)$, ${\it \Gamma}_{\rm \nu}(01)$, ${\it \Gamma}_{\rm \nu}(10)$ und ${\it \Gamma}_{\rm \nu}(11)$ berechnet werden können. | ||
| + | |||
| + | *Hierbei liefert beispielsweise ${\it \Gamma}_{\rm \nu}(01)$ Information über das Symbol $a_{\rm \nu}$ unter der Annahme, dass $a_{\rm \nu +1} = 0$ und $a_{\rm \nu +2} = 1$ sein werden. | ||
| + | |||
| + | *Die minimale Gesamtfehlergröße ${\it \Gamma}_{\rm \nu}(01)$ ist hierbei der kleinere Wert aus dem Vergleich von | ||
| + | :$$\big[{\it \Gamma}_{\nu-1}(00) + \varepsilon_{\nu}(001)\big] \hspace{0.15cm}{\rm und} | ||
| + | \hspace{0.15cm}\big[{\it \Gamma}_{\nu-1}(10) + \varepsilon_{\nu}(101)\big].$$ | ||
| − | Zur Berechnung der minimalen Gesamtfehlergröße ${\it \Gamma}_2(10)$ in den Teilaufgaben (1) und (2) soll von folgenden Zahlenwerten ausgegangen werden: | + | Zur Berechnung der minimalen Gesamtfehlergröße ${\it \Gamma}_2(10)$ in den Teilaufgaben '''(1)''' und '''(2)''' soll von folgenden Zahlenwerten ausgegangen werden: |
| + | * unipolare Amplitudenkoeffizienten: $a_{\rm \nu} ∈ \{0, 1\}$, | ||
| + | * Grundimpulswerte $g_0 = 0.5$, $g_{\rm –1} = 0.3$, $g_{\rm –2} = 0.2$, | ||
| + | |||
| + | * anliegender Detektionsabtastwert: $d_2 = 0.2$, | ||
| + | |||
| + | * Minimale Gesamtfehlergrößen zum Zeitpunkt $\nu = 1$: | ||
| + | :$${\it \Gamma}_{1}(00) = 0.0,\hspace{0.2cm}{\it \Gamma}_{1}(01) = 0.2, \hspace{0.2cm} {\it \Gamma}_{1}(10) = 0.6,\hspace{0.2cm}{\it \Gamma}_{1}(11) = | ||
| + | 1.2 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | In der Grafik ist das vereinfachte Trellisdiagramm für die Zeitpunkte $\nu = 1$ bis $\nu = 8$ dargestellt. | ||
| + | *Blaue Zweige kommen entweder von ${\it \Gamma}_{\rm \nu –1}(00)$ oder von ${\it \Gamma}_{\rm \nu –1}(01)$ und kennzeichnen eine hypothetische „$0$”. | ||
| + | |||
| + | *Dagegen weisen alle roten Zweige – ausgehend von den Zuständen ${\it \Gamma}_{\rm \nu –1}(10)$ bzw. ${\it \Gamma}_{\rm \nu –1}(11)$ – auf das Symbol „$1$” hin. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Viterbi%E2%80%93Empf%C3%A4nger|"Viterbi–Empfänger"]]. Alle Größen sind hier normiert zu verstehen. | ||
| + | |||
| + | *Gehen Sie zudem von unipolaren und gleichwahrscheinlichen Amplitudenkoeffizienten aus: ${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5.$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | { | + | ===Fragebogen=== |
| + | <quiz display=simple> | ||
| + | {Berechnen Sie die folgenden Fehlergrößen: | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\varepsilon_2(010) \ = \ $ { 0.01 3% } |
| − | + | $\varepsilon_2(011) \ = \ $ { 0.09 3% } | |
| + | $\varepsilon_2(110) \ = \ $ { 0.36 3% } | ||
| + | $\varepsilon_2(111) \ = \ $ { 0.64 3% } | ||
| + | {Berechnen Sie die folgenden minimalen Gesamtfehlergrößen: | ||
| + | |type="{}"} | ||
| + | ${\it \Gamma}_2(10) \ = \ $ { 0.21 3% } | ||
| + | ${\it \Gamma}_2(11) \ = \ $ { 0.29 3% } | ||
| + | {Wie lauten die vom Viterbi–Empfänger ausgegebene Symbole? | ||
| + | |type="[]"} | ||
| + | + Die ersten sieben Symbole sind "$1011010$". | ||
| + | - Die ersten sieben Symbole sind "$1101101$". | ||
| + | - Das letzte Symbol $a_8 = 1$ ist sicher. | ||
| + | + Über das Symbol $a_8$ ist noch keine endgültige Aussage möglich. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Die erste Fehlergröße wird wie folgt berechnet: |
| − | + | :$$\varepsilon_{2}(010) = [d_0 - 0 \cdot g_0 - 1 \cdot g_{-1}- 0 \cdot g_{-2}]^2= [0.2 -0.3]^2\hspace{0.15cm}\underline {=0.01} | |
| − | + | \hspace{0.05cm}.$$ | |
| − | + | ||
| − | + | Entsprechend gilt für die weiteren Fehlergrößen: | |
| − | ''' | + | :$$\varepsilon_{2}(011) \ = \ [0.2 -0.3- 0.2]^2\hspace{0.15cm}\underline {=0.09}\hspace{0.05cm},$$ |
| − | ''' | + | :$$\varepsilon_{2}(110) \ = \ [0.2 -0.5- 0.3]^2\hspace{0.15cm}\underline {=0.36}\hspace{0.05cm},$$ |
| + | :$$\varepsilon_{2}(111) \ = \ [0.2 -0.5- 0.3-0.2]^2\hspace{0.15cm}\underline {=0.64} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' Die Aufgabe ist, jeweils den minimalen Wert von zwei Vergleichswerten zu finden: | ||
| + | :$${\it \Gamma}_{2}(10) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(01) + \varepsilon_{2}(010), | ||
| + | \hspace{0.2cm}{\it \Gamma}_{1}(11) + \varepsilon_{2}(110)\right] = {\rm Min}\left[0.2+ 0.01, 1.2 + 0.36\right]\hspace{0.15cm}\underline {= 0.21} | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$${\it \Gamma}_{2}(11) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(01) + \varepsilon_{2}(011), | ||
| + | \hspace{0.2cm}{\it \Gamma}_{1}(11) + \varepsilon_{2}(111)\right] = {\rm Min}\left[0.2+ 0.09, 1.2 + 0.64\right]\hspace{0.15cm}\underline {= 0.29} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Richtig sind der <u>erste und der letzte Lösungsvorschlag</u>: | ||
| + | *Die Folge "$1011010$" erkennt man aus dem durchgehenden Pfad: „Rot – Blau – Rot – Rot – Blau – Rot – Blau”. | ||
| + | |||
| + | *Dagegen kann über das Symbol $a_8$ zum Zeitpunkt $\nu = 8$ noch keine endgültige Aussage gemacht werden: | ||
| + | |||
| + | *Nur unter der Hypothese $a_9 = 1$ <u>und</u> $a_{\rm 10} = 1$ würde man sich für $a_8 = 0$ entscheiden, bei anderen Hypothesen für $a_8 = 1$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 5. Juli 2022, 12:08 Uhr
Wir gehen von den Grundimpulswerten $g_0\ne 0$, $g_{\rm –1}\ne 0$ and $g_{\rm –2}\ne 0$ aus:
- Das bedeutet, dass die Entscheidung über das Symbol $a_{\rm \nu}$ auch durch die nachfolgenden Koeffizienten $a_{\rm \nu +1}$ und $a_{\rm \nu +2}$ beeinflusst wird.
- Damit sind für jeden Zeitpunkt $\nu$ genau acht Fehlergrößen $\varepsilon_{\rm \nu}$ zu bestimmen, aus denen die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(00)$, ${\it \Gamma}_{\rm \nu}(01)$, ${\it \Gamma}_{\rm \nu}(10)$ und ${\it \Gamma}_{\rm \nu}(11)$ berechnet werden können.
- Hierbei liefert beispielsweise ${\it \Gamma}_{\rm \nu}(01)$ Information über das Symbol $a_{\rm \nu}$ unter der Annahme, dass $a_{\rm \nu +1} = 0$ und $a_{\rm \nu +2} = 1$ sein werden.
- Die minimale Gesamtfehlergröße ${\it \Gamma}_{\rm \nu}(01)$ ist hierbei der kleinere Wert aus dem Vergleich von
- $$\big[{\it \Gamma}_{\nu-1}(00) + \varepsilon_{\nu}(001)\big] \hspace{0.15cm}{\rm und} \hspace{0.15cm}\big[{\it \Gamma}_{\nu-1}(10) + \varepsilon_{\nu}(101)\big].$$
Zur Berechnung der minimalen Gesamtfehlergröße ${\it \Gamma}_2(10)$ in den Teilaufgaben (1) und (2) soll von folgenden Zahlenwerten ausgegangen werden:
- unipolare Amplitudenkoeffizienten: $a_{\rm \nu} ∈ \{0, 1\}$,
- Grundimpulswerte $g_0 = 0.5$, $g_{\rm –1} = 0.3$, $g_{\rm –2} = 0.2$,
- anliegender Detektionsabtastwert: $d_2 = 0.2$,
- Minimale Gesamtfehlergrößen zum Zeitpunkt $\nu = 1$:
- $${\it \Gamma}_{1}(00) = 0.0,\hspace{0.2cm}{\it \Gamma}_{1}(01) = 0.2, \hspace{0.2cm} {\it \Gamma}_{1}(10) = 0.6,\hspace{0.2cm}{\it \Gamma}_{1}(11) = 1.2 \hspace{0.05cm}.$$
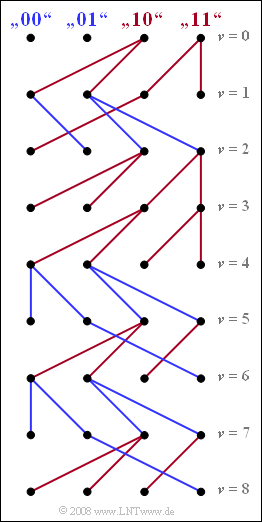
In der Grafik ist das vereinfachte Trellisdiagramm für die Zeitpunkte $\nu = 1$ bis $\nu = 8$ dargestellt.
- Blaue Zweige kommen entweder von ${\it \Gamma}_{\rm \nu –1}(00)$ oder von ${\it \Gamma}_{\rm \nu –1}(01)$ und kennzeichnen eine hypothetische „$0$”.
- Dagegen weisen alle roten Zweige – ausgehend von den Zuständen ${\it \Gamma}_{\rm \nu –1}(10)$ bzw. ${\it \Gamma}_{\rm \nu –1}(11)$ – auf das Symbol „$1$” hin.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Viterbi–Empfänger". Alle Größen sind hier normiert zu verstehen.
- Gehen Sie zudem von unipolaren und gleichwahrscheinlichen Amplitudenkoeffizienten aus: ${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5.$
Fragebogen
Musterlösung
(1) Die erste Fehlergröße wird wie folgt berechnet:
- $$\varepsilon_{2}(010) = [d_0 - 0 \cdot g_0 - 1 \cdot g_{-1}- 0 \cdot g_{-2}]^2= [0.2 -0.3]^2\hspace{0.15cm}\underline {=0.01} \hspace{0.05cm}.$$
Entsprechend gilt für die weiteren Fehlergrößen:
- $$\varepsilon_{2}(011) \ = \ [0.2 -0.3- 0.2]^2\hspace{0.15cm}\underline {=0.09}\hspace{0.05cm},$$
- $$\varepsilon_{2}(110) \ = \ [0.2 -0.5- 0.3]^2\hspace{0.15cm}\underline {=0.36}\hspace{0.05cm},$$
- $$\varepsilon_{2}(111) \ = \ [0.2 -0.5- 0.3-0.2]^2\hspace{0.15cm}\underline {=0.64} \hspace{0.05cm}.$$
(2) Die Aufgabe ist, jeweils den minimalen Wert von zwei Vergleichswerten zu finden:
- $${\it \Gamma}_{2}(10) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(01) + \varepsilon_{2}(010), \hspace{0.2cm}{\it \Gamma}_{1}(11) + \varepsilon_{2}(110)\right] = {\rm Min}\left[0.2+ 0.01, 1.2 + 0.36\right]\hspace{0.15cm}\underline {= 0.21} \hspace{0.05cm},$$
- $${\it \Gamma}_{2}(11) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(01) + \varepsilon_{2}(011), \hspace{0.2cm}{\it \Gamma}_{1}(11) + \varepsilon_{2}(111)\right] = {\rm Min}\left[0.2+ 0.09, 1.2 + 0.64\right]\hspace{0.15cm}\underline {= 0.29} \hspace{0.05cm}.$$
(3) Richtig sind der erste und der letzte Lösungsvorschlag:
- Die Folge "$1011010$" erkennt man aus dem durchgehenden Pfad: „Rot – Blau – Rot – Rot – Blau – Rot – Blau”.
- Dagegen kann über das Symbol $a_8$ zum Zeitpunkt $\nu = 8$ noch keine endgültige Aussage gemacht werden:
- Nur unter der Hypothese $a_9 = 1$ und $a_{\rm 10} = 1$ würde man sich für $a_8 = 0$ entscheiden, bei anderen Hypothesen für $a_8 = 1$.