Loading [MathJax]/jax/output/HTML-CSS/fonts/TeX/fontdata.js

Aufgaben:Aufgabe 4.2Z: Multiplikation mit Sinussignal: Unterschied zwischen den Versionen

Aus LNTwww
Wechseln zu:Navigation, Suche
 
(13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
  
−
{{quiz-Header|Buchseite=Signaldarstellung/Unterschiede und Gemeinsamkeiten von TP- und BP-Signalen
+
{{quiz-Header|Buchseite=Signaldarstellung/Grundsätzliches_zu_Tiefpass-_und_Bandpass-Signalen
 
}}
 
}}
  
−
[[Datei:P_ID697__Sig_Z_4_2_neu.png|right|Modulation mit Sinussignal]]
+
[[Datei:P_ID697__Sig_Z_4_2_neu.png|right|frame|Spektralfunktionen  Q(f)  und  Z(f)]]
−
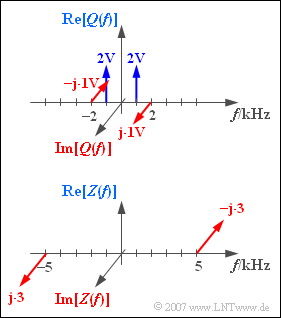
Betrachtet wird ein periodisches Nachrichtensignal q(t), dessen Spektralfunktion Q(f) in der oberen Grafik zu sehen ist.
+
Betrachtet wird ein periodisches Nachrichtensignal  q(t), dessen Spektralfunktion  Q(f)  in der oberen Grafik zu sehen ist.
  
−
Eine Multiplikation mit dem dimensionslosen Träger z(t), dessen Spektrum Z(f) ebenfalls dargestellt ist, führt zum Signal s(t)=q(t)⋅z(t).
+
Eine Multiplikation mit dem dimensionslosen Träger  z(t), dessen Spektrum  Z(f)  ebenfalls dargestellt ist, führt zum Signal  s(t)=q(t)⋅z(t).
 +
 
 +
In dieser Aufgabe soll die Spektralfunktion  S(f)  dieses Signals ermittelt werden, wobei die Lösung entweder im Zeit– oder im Frequenzbereich erfolgen kann.
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
''Hinweis:''
 +
*Die Aufgabe gehört zum  Kapitel  [[Signaldarstellung/Grundsätzliches_zu_Tiefpass-_und_Bandpass-Signalen|Grundsätzliches zu Tiefpass- und Bandpass-Signalen]].
 +
  
−
In dieser Aufgabe soll die Spektralfunktion S(f) dieses Signals ermittelt werden, wobei die Lösung entweder im Zeit- oder im Frequenzbereich erfolgen kann.
 
  
−
''Hinweise:''
 
−
*Die Aufgabe gehört zum  Kapitel [[Unterschiede_und_Gemeinsamkeiten_von_TP-_und_BP-Signalen|Signaldarstellung/Unterschiede und Gemeinsamkeiten von TP- und BP-Signalen.
 
−
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
 
  
  
Zeile 18: Zeile 26:
  
 
<quiz display=simple>
 
<quiz display=simple>
−
{Geben Sie das Quellensignal q(t) in analytischer Form an. Welche Werte ergeben sich für t=0 und t=0.125ms?
+
{Geben Sie das Quellensignal&nbsp; q(t)&nbsp; in analytischer Form an.&nbsp; Welche Werte ergeben sich für&nbsp; t=0&nbsp; und&nbsp; t=0.125ms?
 
|type="{}"}
 
|type="{}"}
−
q(t=0) &nbsp;= { 4 3% } &nbsp;V
+
$q(t = 0)\ = \ $ { 4 3% } &nbsp;V
−
q(t=0.125ms) &nbsp;= { 0.828 3% } V
+
$q(t = 0.125 \,\text{ms})\ = \ { 0.828 3% }\text{V}$
  
  
−
{Wie lautet das (dimensionslose) Trägersignal z(t)? Wie groß ist dessen Maximalwert?
+
{Wie lautet das (dimensionslose) Trägersignal&nbsp; z(t)?&nbsp; Wie groß ist dessen Maximalwert?
 
|type="{}"}
 
|type="{}"}
−
zmax &nbsp;= { 6 3% }
+
$z_{\rm max}\ = \ $ { 6 3% }
  
  
−
{Berechnen Sie die Spektrum S(f) getrennt nach Real– und Imaginärteil. Bei welchen Frequenzen gibt es Linien mit einem Realteil ≠0?
+
{Berechnen Sie die Spektrum&nbsp; S(f)&nbsp; getrennt nach Real– und Imaginärteil.&nbsp; Bei welchen Frequenzen gibt es Linien mit einem Realteil ungleich Null?
 
|type="[]"}
 
|type="[]"}
 
+ 3 kHz,
 
+ 3 kHz,
Zeile 53: Zeile 61:
 
===Musterlösung===
 
===Musterlösung===
 
{{ML-Kopf}}
 
{{ML-Kopf}}
−
'''1.'''  Das Nachrichtensignal lässt sich mit den Abkürzungen f1=1kHz und T1=1/f1=1ms wie folgt darstellen (beachten Sie, dass f2=2f1 gilt):
+
'''(1)'''&nbsp; Das Nachrichtensignal lässt sich mit den Abkürzungen&nbsp; $f_1 = 1\ \text{kHz}$&nbsp; und&nbsp; $T_1 = 1/f_1 = 1 \ \text{ms}$&nbsp; wie folgt darstellen&nbsp; $($es gilt&nbsp; $f_2 = 2f_1)$:
 
:$$q(t ) = 4\hspace{0.05cm}{\rm V}
 
:$$q(t ) = 4\hspace{0.05cm}{\rm V}
 
  \cdot  {\cos} ( 2 \pi f_1 t) - 2\hspace{0.05cm}{\rm V}
 
  \cdot  {\cos} ( 2 \pi f_1 t) - 2\hspace{0.05cm}{\rm V}
 
  \cdot  {\sin} ( 4 \pi f_1 t)=
 
  \cdot  {\sin} ( 4 \pi f_1 t)=
 
  4\hspace{0.05cm}{\rm V}
 
  4\hspace{0.05cm}{\rm V}
−
  \cdot  {\cos} ( 2 \pi \frac{t}{T_1}) - 2\hspace{0.05cm}{\rm V}
+
  \cdot  {\cos} ( 2 \pi {t}/{T_1}) - 2\hspace{0.05cm}{\rm V}
−
  \cdot  {\sin} ( 4 \pi \frac{t}{T_1}) .$$
+
  \cdot  {\sin} ( 4 \pi {t}/{T_1}) .$$
−
Zum Zeitpunkt t=0 verschwindet der zweite Anteil und es ergibt sich q(t=0)=4V_. Dagegen erhält man für t=0.125ms=T1/8:
+
*Zum Zeitpunkt&nbsp; t=0&nbsp; verschwindet der zweite Anteil und es ergibt sich&nbsp; $q(t = 0)\; \underline{= 4 \ \text{V}}$.  
 +
*Dagegen erhält man für&nbsp; $t = 0.125 \ \text{ms} = T_1/8$:
 
:$$q(t = 0.125{\rm ms})  =  4\hspace{0.05cm}{\rm V}
 
:$$q(t = 0.125{\rm ms})  =  4\hspace{0.05cm}{\rm V}
−
  \cdot  {\cos} ( \frac{\pi}{4}) - 2\hspace{0.05cm}{\rm V}
+
  \cdot  {\cos} ( {\pi}/{4}) - 2\hspace{0.05cm}{\rm V}
−
  \cdot  {\sin} ( \frac{\pi}{2}) = \frac
+
  \cdot  {\sin} ( {\pi}/{2}) = \frac
 
  {4\hspace{0.05cm}{\rm V}}{\sqrt{2}} - 2\hspace{0.05cm}{\rm V} \hspace{0.15 cm}\underline{=
 
  {4\hspace{0.05cm}{\rm V}}{\sqrt{2}} - 2\hspace{0.05cm}{\rm V} \hspace{0.15 cm}\underline{=
 
  0.828 \hspace{0.05cm}{\rm V}}.$$
 
  0.828 \hspace{0.05cm}{\rm V}}.$$
  
−
'''2.''' Entsprechend dem rein imaginären Spektrum Z(f) und den Impulsgewichten ±3 muss gelten:
+
 
 +
'''(2)'''&nbsp; Entsprechend dem rein imaginären Spektrum&nbsp; Z(f)&nbsp; und den Impulsgewichten&nbsp; ±3&nbsp; muss gelten:
 
:$$z(t )  = 6 \cdot  {\sin} ( 2 \pi \cdot 5\hspace{0.05cm}{\rm
 
:$$z(t )  = 6 \cdot  {\sin} ( 2 \pi \cdot 5\hspace{0.05cm}{\rm
 
kHz})\hspace{0.5cm}\Rightarrow \hspace{0.5cm} z_{\rm max}\hspace{0.15 cm}\underline{ = 6} .$$
 
kHz})\hspace{0.5cm}\Rightarrow \hspace{0.5cm} z_{\rm max}\hspace{0.15 cm}\underline{ = 6} .$$
  
−
'''3.''' und '''4.''' Die Spektralfunktion S(f) ergibt sich aus der Faltung zwischen Q(f) und Z(f). Man erhält:
+
 
 +
[[Datei:P_ID706__Sig_Z_4_2_c.png|right|frame|Diskretes Bandpass&ndash;Spektrum]]
 +
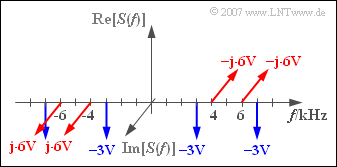
'''(3)'''&nbsp; Die Spektralfunktion&nbsp; S(f)&nbsp; ergibt sich aus der Faltung zwischen&nbsp; Q(f)&nbsp; und&nbsp; Z(f). Man erhält:
 
:$$S(f)  = - 3{\rm j} \cdot Q(f- f_{\rm T}) + 3{\rm j} \cdot Q(f+
 
:$$S(f)  = - 3{\rm j} \cdot Q(f- f_{\rm T}) + 3{\rm j} \cdot Q(f+
 
f_{\rm T}).$$
 
f_{\rm T}).$$
−
[[Datei:P_ID706__Sig_Z_4_2_c.png|right|]]
+
Es ergeben sich Spektrallinien bei  
−
Es ergeben sich Spektrallinien bei $3\ \text{kHz}\ (–3V), 4\ \text{kHz} (–j \cdot 6V), 6\ \text{kHz} (–j \cdot 6V)$ sowie $7\ \text{kHz}\ (–3V)$, und dazu noch die konjugiert–komplexen Anteile bei negativen Frequenzen:
+
*$3\ \text{kHz}\ (–3\ {\rm V})$,  
 +
*$4\ \text{kHz} (–{\rm j} \cdot 6\ {\rm V})$,  
 +
*$6\ \text{kHz} (–{\rm j} \cdot 6\ {\rm V})$,
 +
* $7\ \text{kHz}\ (–3\ {\rm V})$.
 +
 
 +
 +
Dazu noch die konjugiert–komplexen Anteile bei negativen Frequenzen.
 +
 
 +
Linien mit reellen Gewichten bei&nbsp; ±3 kHz_&nbsp; <u>und</u>&nbsp; ±7 kHz_.
 +
 
 +
 
  
−
:* Teilaufgabe (3): Linien mit reellen Gewichten bei $\underline{\pm 3 \text{kHz}}<u>und</u>\underline{\pm 7 \text{kHz}}$,
+
'''(4)'''&nbsp;  Imaginäre Linien treten bei&nbsp; $\underline{\pm 4 \ \text{kHz}}$&nbsp; <u>und</u>&nbsp; $\underline{\pm 6 \ \text{kHz}}$ auf.
  
−
:* Teilaufgabe (4): Imaginäre Linien bei ±4kHz_ <u>und</u> ±6kHz_.
+
Eine alternative Möglichkeit zur Lösung dieser Aufgabe ist die Anwendung trigonometrischer Gleichungen.  
  
−
Eine alternative Möglichkeit zur Lösung dieser Aufgabe ist die Anwendung trigonometrischer Gleichungen. Im Folgenden bezeichnet zum Beispiel f5=5kHz. Dann gilt:
+
Im Folgenden bezeichnet zum Beispiel&nbsp; f5=5 kHz. Dann gilt:
 
:$$4\hspace{0.05cm}{\rm V}
 
:$$4\hspace{0.05cm}{\rm V}
 
  \cdot  {\cos} ( 2 \pi f_1 \hspace{0.03cm}t) \cdot 3
 
  \cdot  {\cos} ( 2 \pi f_1 \hspace{0.03cm}t) \cdot 3
 
  \cdot  {\sin} ( 2 \pi f_5 \hspace{0.03cm} t)=
 
  \cdot  {\sin} ( 2 \pi f_5 \hspace{0.03cm} t)=
−
  \frac{12\hspace{0.05cm}{\rm V}}{2}\cdot \left[{\sin} ( 2 \pi f_4 \hspace{0.03cm}
+
  \frac{12\hspace{0.05cm}{\rm V}}{2}\cdot \big[{\sin} ( 2 \pi f_4 \hspace{0.03cm}
−
  t)+ {\sin} ( 2 \pi f_6 \hspace{0.03cm} t)\right],$$
+
  t)+ {\sin} ( 2 \pi f_6 \hspace{0.03cm} t)\big],$$
 
:$$-2\hspace{0.05cm}{\rm V}
 
:$$-2\hspace{0.05cm}{\rm V}
 
  \cdot  {\sin} ( 2 \pi f_2 \hspace{0.03cm}t) \cdot 3
 
  \cdot  {\sin} ( 2 \pi f_2 \hspace{0.03cm}t) \cdot 3
 
  \cdot  {\sin} ( 2 \pi f_5 \hspace{0.03cm} t)=
 
  \cdot  {\sin} ( 2 \pi f_5 \hspace{0.03cm} t)=
−
  \frac{-6\hspace{0.05cm}{\rm V}}{2}\cdot \left[{\cos} ( 2 \pi f_3 \hspace{0.03cm}
+
  \frac{-6\hspace{0.05cm}{\rm V}}{2}\cdot \big[{\cos} ( 2 \pi f_3 \hspace{0.03cm}
−
  t)+ {\cos} ( 2 \pi f_7 \hspace{0.03cm} t)\right].$$
+
  t)+ {\cos} ( 2 \pi f_7 \hspace{0.03cm} t)\big].$$
−
Aus der ersten Gleichung ergeben sich folgende Spektrallinien:  
+
 
 +
*Aus der ersten Gleichung ergeben sich folgende Spektrallinien:  
 +
 
 +
:* bei&nbsp; +f4&nbsp; bzw.&nbsp; −f4&nbsp; mit den Gewichten&nbsp; –{\rm j} \cdot 3\ {\rm V}&nbsp; bzw.&nbsp; +{\rm j}\cdot 3 \ {\rm V},
 +
 
 +
:* bei&nbsp; +f_6&nbsp; bzw.&nbsp; -f_6&nbsp; mit den Gewichten&nbsp; –{\rm j} \cdot 3 \ {\rm V}&nbsp; bzw.&nbsp; +{\rm j} \cdot 3 \ {\rm V}.
  
−
:* bei $f_4$ bzw. $–f_4$ mit den Gewichten $–j \cdot 3V$ bzw. +j \cdot 3V,
+
*Die zweite Gleichung liefert insgesamt vier Diraclinien&nbsp; (alle&nbsp; $6 \ {\rm V}$, reell und negativ) bei&nbsp; $\pm f_3$&nbsp; und&nbsp; $\pm f_7$.  
  
−
:* bei f_6 bzw. –f_6 mit den Gewichten –j \cdot 3V bzw. +j \cdot 3V.
 
  
−
Die zweite Gleichung liefert insgesamt 4 Diraclinien (alle 6 V, reell und negativ) bei \pm f_3 und \pm f_7. Ein Vergleich mit obiger Skizze zeigt, dass beide Lösungswege zum gleichen Ergebnis führen.
+
Ein Vergleich mit obiger Skizze zeigt, dass beide Lösungswege zum gleichen Ergebnis führen.
 
{{ML-Fuß}}
 
{{ML-Fuß}}
  

Aktuelle Version vom 3. Mai 2021, 18:15 Uhr

Spektralfunktionen  Q(f)  und  Z(f)

Betrachtet wird ein periodisches Nachrichtensignal  q(t), dessen Spektralfunktion  Q(f)  in der oberen Grafik zu sehen ist.

Eine Multiplikation mit dem dimensionslosen Träger  z(t), dessen Spektrum  Z(f)  ebenfalls dargestellt ist, führt zum Signal  s(t) = q(t) \cdot z(t).

In dieser Aufgabe soll die Spektralfunktion  S(f)  dieses Signals ermittelt werden, wobei die Lösung entweder im Zeit– oder im Frequenzbereich erfolgen kann.




Hinweis:



Fragebogen

1

Geben Sie das Quellensignal  q(t)  in analytischer Form an.  Welche Werte ergeben sich für  t = 0  und  t = 0.125\, \text{ms}?

q(t = 0)\ = \

 \text{V}
q(t = 0.125 \,\text{ms})\ = \

\text{V}

2

Wie lautet das (dimensionslose) Trägersignal  z(t)?  Wie groß ist dessen Maximalwert?

z_{\rm max}\ = \

3

Berechnen Sie die Spektrum  S(f)  getrennt nach Real– und Imaginärteil.  Bei welchen Frequenzen gibt es Linien mit einem Realteil ungleich Null?

3\ \text{kHz},
4\ \text{kHz},
5\ \text{kHz},
6\ \text{kHz},
7\ \text{kHz}.

4

Bei welchen Frequenzen treten rein imaginäre Spektrallinien auf?

3\ \text{kHz},
4\ \text{kHz},
5\ \text{kHz},
6\ \text{kHz},
7\ \text{kHz}.


Musterlösung

Musterlösung

(1)  Das Nachrichtensignal lässt sich mit den Abkürzungen  f_1 = 1\ \text{kHz}  und  T_1 = 1/f_1 = 1 \ \text{ms}  wie folgt darstellen  (es gilt  f_2 = 2f_1):

q(t ) = 4\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi f_1 t) - 2\hspace{0.05cm}{\rm V} \cdot {\sin} ( 4 \pi f_1 t)= 4\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi {t}/{T_1}) - 2\hspace{0.05cm}{\rm V} \cdot {\sin} ( 4 \pi {t}/{T_1}) .
  • Zum Zeitpunkt  t = 0  verschwindet der zweite Anteil und es ergibt sich  q(t = 0)\; \underline{= 4 \ \text{V}}.
  • Dagegen erhält man für  t = 0.125 \ \text{ms} = T_1/8:
q(t = 0.125{\rm ms}) = 4\hspace{0.05cm}{\rm V} \cdot {\cos} ( {\pi}/{4}) - 2\hspace{0.05cm}{\rm V} \cdot {\sin} ( {\pi}/{2}) = \frac {4\hspace{0.05cm}{\rm V}}{\sqrt{2}} - 2\hspace{0.05cm}{\rm V} \hspace{0.15 cm}\underline{= 0.828 \hspace{0.05cm}{\rm V}}.


(2)  Entsprechend dem rein imaginären Spektrum  Z(f)  und den Impulsgewichten  \pm 3  muss gelten:

z(t ) = 6 \cdot {\sin} ( 2 \pi \cdot 5\hspace{0.05cm}{\rm kHz})\hspace{0.5cm}\Rightarrow \hspace{0.5cm} z_{\rm max}\hspace{0.15 cm}\underline{ = 6} .


Diskretes Bandpass–Spektrum

(3)  Die Spektralfunktion  S(f)  ergibt sich aus der Faltung zwischen  Q(f)  und  Z(f). Man erhält:

S(f) = - 3{\rm j} \cdot Q(f- f_{\rm T}) + 3{\rm j} \cdot Q(f+ f_{\rm T}).

Es ergeben sich Spektrallinien bei

  • 3\ \text{kHz}\ (–3\ {\rm V}),
  • 4\ \text{kHz} (–{\rm j} \cdot 6\ {\rm V}),
  • 6\ \text{kHz} (–{\rm j} \cdot 6\ {\rm V}),
  • 7\ \text{kHz}\ (–3\ {\rm V}).


Dazu noch die konjugiert–komplexen Anteile bei negativen Frequenzen.

Linien mit reellen Gewichten bei  \underline{\pm 3 \ \text{kHz}}  und  \underline{\pm 7 \ \text{kHz}}.


(4)  Imaginäre Linien treten bei  \underline{\pm 4 \ \text{kHz}}  und  \underline{\pm 6 \ \text{kHz}} auf.

Eine alternative Möglichkeit zur Lösung dieser Aufgabe ist die Anwendung trigonometrischer Gleichungen.

Im Folgenden bezeichnet zum Beispiel  f_5 = 5 \text{ kHz}. Dann gilt:

4\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi f_1 \hspace{0.03cm}t) \cdot 3 \cdot {\sin} ( 2 \pi f_5 \hspace{0.03cm} t)= \frac{12\hspace{0.05cm}{\rm V}}{2}\cdot \big[{\sin} ( 2 \pi f_4 \hspace{0.03cm} t)+ {\sin} ( 2 \pi f_6 \hspace{0.03cm} t)\big],
-2\hspace{0.05cm}{\rm V} \cdot {\sin} ( 2 \pi f_2 \hspace{0.03cm}t) \cdot 3 \cdot {\sin} ( 2 \pi f_5 \hspace{0.03cm} t)= \frac{-6\hspace{0.05cm}{\rm V}}{2}\cdot \big[{\cos} ( 2 \pi f_3 \hspace{0.03cm} t)+ {\cos} ( 2 \pi f_7 \hspace{0.03cm} t)\big].
  • Aus der ersten Gleichung ergeben sich folgende Spektrallinien:
  • bei  +f_4  bzw.  -f_4  mit den Gewichten  –{\rm j} \cdot 3\ {\rm V}  bzw.  +{\rm j}\cdot 3 \ {\rm V},
  • bei  +f_6  bzw.  -f_6  mit den Gewichten  –{\rm j} \cdot 3 \ {\rm V}  bzw.  +{\rm j} \cdot 3 \ {\rm V}.
  • Die zweite Gleichung liefert insgesamt vier Diraclinien  (alle  6 \ {\rm V}, reell und negativ) bei  \pm f_3  und  \pm f_7.


Ein Vergleich mit obiger Skizze zeigt, dass beide Lösungswege zum gleichen Ergebnis führen.

Abgerufen von „http://www.lntwww.de/index.php?title=Aufgaben:Aufgabe_4.2Z:_Multiplikation_mit_Sinussignal&oldid=31882“
  • Powered by MediaWiki