Aufgaben:Aufgabe 3.5Z: Integration von Diracfunktionen: Unterschied zwischen den Versionen
Aus LNTwww
| (12 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID515__Sig_Z_3_5_neu.png|right|Integration von Diracfunktionen ]] | + | [[Datei:P_ID515__Sig_Z_3_5_neu.png|right|frame|Integration von Diracfunktionen ]] |
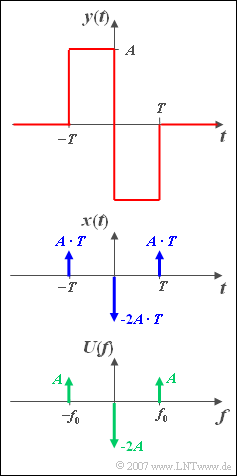
| − | Wie in [[Aufgaben:3.5_Differentiation_eines_Dreicksignals|Aufgabe 3.5]] soll das Spektrum ${Y(f)}$ des Signals | + | Wie in der [[Aufgaben:3.5_Differentiation_eines_Dreicksignals|Aufgabe 3.5]] soll das Spektrum ${Y(f)}$ des Signals |
:$$y( t ) = \left\{ \begin{array}{c} A \\ - A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {{\rm{f \ddot{u}r}}} \\ {{\rm{f\ddot{u} r}}} \\ {\rm{sonst.}} \\ \end{array}\;\begin{array}{*{20}c} { - T \le t < 0,} \\ {0 < t \le T,} \\ {} \\\end{array}$$ | :$$y( t ) = \left\{ \begin{array}{c} A \\ - A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {{\rm{f \ddot{u}r}}} \\ {{\rm{f\ddot{u} r}}} \\ {\rm{sonst.}} \\ \end{array}\;\begin{array}{*{20}c} { - T \le t < 0,} \\ {0 < t \le T,} \\ {} \\\end{array}$$ | ||
| − | ermittelt werden. Es gelte wieder $A = 1 \,\text{V}$ und $T = 0.5 \,\text{ms}$. | + | ermittelt werden. Es gelte wieder $A = 1 \,\text{V}$ und $T = 0.5 \,\text{ms}$. |
| − | Ausgegangen wird vom Zeitsignal $ | + | Ausgegangen wird vom Zeitsignal ${x(t)}$ gemäß der mittleren Skizze, das sich aus drei Diracimpulsen bei $–T$, $0$ und $+T$ mit den Impulsgewichte ${AT}$, $-2{AT}$ und ${AT}$ zusammensetzt. |
| − | Die Spektralfunktion $ | + | Die Spektralfunktion ${X(f)}$ kann durch Anwendung des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Vertauschungssatz|Vertauschungssatzes]] direkt angegeben werden, wenn man berücksichtigt, dass die zu ${U(f)}$ gehörige Zeitfunktion wie folgt lautet (siehe untere Skizze): |
:$$u( t ) = - 2A + 2A \cdot \cos ( {2{\rm{\pi }}f_0 t} ).$$ | :$$u( t ) = - 2A + 2A \cdot \cos ( {2{\rm{\pi }}f_0 t} ).$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation|Gesetzmäßigkeiten der Fouriertransformation]]. | + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation|Gesetzmäßigkeiten der Fouriertransformation]]. |
| − | *Alle | + | *Alle diese Gesetzmäßigkeiten werden im Lernvideo [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|Gesetzmäßigkeiten der Fouriertransformation]] an Beispielen verdeutlicht. |
| − | * | + | *Zwischen ${x(t)}$ und ${y(t)}$ besteht folgender Zusammenhang: |
| − | |||
| − | |||
| − | |||
| − | |||
:$$y( t ) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )}\, {\rm d}\tau .$$ | :$$y( t ) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )}\, {\rm d}\tau .$$ | ||
| − | Der Integrationssatz lautet in entsprechend angepasster Form: | + | *Der [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Integrationssatz|Integrationssatz]] lautet in entsprechend angepasster Form: |
| − | :$$\frac{1}{T}\cdot \hspace{-0.1cm} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )}\,\, {\rm d}\tau\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f )\left( {\frac{1}{{{\rm{j}}2{\rm{\pi }}fT}} + \frac{1}{2T}\cdot {\rm \delta} ( f )} \right).$$ | + | :$$\frac{1}{T}\cdot \hspace{-0.1cm} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )}\,\, {\rm d}\tau\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ X( f ) \cdot \left( {\frac{1}{{{\rm{j}}\cdot 2{\rm{\pi }\cdot }fT}} + \frac{1}{2T}\cdot {\rm \delta} ( f )} \right).$$ |
| − | + | ||
| − | |||
| − | |||
| Zeile 32: | Zeile 33: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie die Spektralfunktion $ | + | {Berechnen Sie die Spektralfunktion ${X(f)}$. Wie groß ist deren Betrag bei den Frequenzen $f = 0$ und $f = 1\, \text{kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | $| | + | $|{X(f = 0)}| \ = \ $ { 0. } $\text{mV/Hz}$ |
| − | $| | + | $|{X(f = 1\, \text{kHz})}|\ = \ $ { 2 3% } $\text{mV/Hz}$ |
| − | {Berechnen Sie die Spektralfunktion $ | + | {Berechnen Sie die Spektralfunktion ${Y(f)}$. Welche Werte ergeben sich bei den Frequenzen $f = 0$ und $f = 1\, \text{kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | $| | + | $|{Y(f = 0)}|\ = \ $ { 0. } $\text{mV/Hz}$ |
| − | $| | + | $|{Y(f = 1\, \text{kHz})}| \ = \ $ { 0.636 3% } $\text{mV/Hz}$ |
| Zeile 49: | Zeile 50: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Im Angabenteil zur Aufgabe finden Sie die Fourierkorrespondenz zwischen ${u(t)}$ und ${U(f)}$. |
| + | *Da sowohl die Zeitfunktionen ${u(t)}$ und ${x(t)}$ als auch die dazugehörigen Spektren ${U(f)}$ und ${X(f)}$ gerade und reell sind, kann man ${X(f)}$ durch Anwendung des Vertauschungssatzes leicht berechnen: | ||
:$$X( f ) = - 2 \cdot A \cdot T + 2 \cdot A \cdot T \cdot \cos \left( {{\rm{2\pi }}fT} \right).$$ | :$$X( f ) = - 2 \cdot A \cdot T + 2 \cdot A \cdot T \cdot \cos \left( {{\rm{2\pi }}fT} \right).$$ | ||
| − | Wegen der Beziehung $ | + | *Wegen der Beziehung $\sin^{2}(\alpha) = (1 – \cos(\alpha))/2$ kann hierfür auch geschrieben werden: |
:$$X( f ) = - 4 \cdot A \cdot T \cdot \sin ^2 ( {{\rm{\pi }}fT} ).$$ | :$$X( f ) = - 4 \cdot A \cdot T \cdot \sin ^2 ( {{\rm{\pi }}fT} ).$$ | ||
| − | Bei der Frequenz $f = 0$ hat $ | + | :*Bei der Frequenz $f = 0$ hat ${x(t)}$ keine Spektralanteile ⇒ ${X(f = 0)} \;\underline{= 0}$. |
| − | :$$X( f = 1\;{\rm{kHz}} ) = - 4 \cdot A \cdot T = -2 \cdot 10^{ - 3} \;{\rm{V/Hz}}\ | + | :*Für $f = 1 \,\text{kHz}$ – also $f \cdot T = 0.5$ – gilt dagegen: |
| − | |X( {f = 1\;{\rm{kHz}}} )| \hspace{0.15 cm}\underline{= 2 | + | :$$X( f = 1\;{\rm{kHz}} ) = - 4 \cdot A \cdot T = -2 \cdot 10^{ - 3} \;{\rm{V/Hz}}\; \Rightarrow \; |
| + | |X( {f = 1\;{\rm{kHz}}} )| \hspace{0.15 cm}\underline{= 2 \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
| + | |||
| + | |||
| − | '''2 | + | '''(2)''' Das Spektrum ${Y(f)}$ kann aus ${X(f)}$ durch Anwendung des Integrationssatzes ermittelt werden. |
| + | *Wegen ${X(f = 0)} = 0$ muss die Diracfunktion bei der Frequenz $f = 0$ nicht berücksichtigt werden und man erhält: | ||
:$$Y( f ) = \frac{X( f )}{{{\rm{j}} \cdot 2{\rm{\pi }}fT}} = \frac{{ - 4 \cdot A \cdot T \cdot \sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{j}}\cdot 2{\rm{\pi }}fT}} = 2{\rm{j}} \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$ | :$$Y( f ) = \frac{X( f )}{{{\rm{j}} \cdot 2{\rm{\pi }}fT}} = \frac{{ - 4 \cdot A \cdot T \cdot \sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{j}}\cdot 2{\rm{\pi }}fT}} = 2{\rm{j}} \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$ | ||
| − | Es ergibt sich selbstverständlich das gleiche Ergebnis wie in Aufgabe | + | *Es ergibt sich selbstverständlich das gleiche Ergebnis wie in der [[Aufgaben:3.5_Differentiation_eines_Dreicksignals|Aufgabe 3.5]]: |
| − | :$$|Y( {f = 1\;{\rm{kHz}}} )| = \frac{4 \cdot A \cdot T}{\rm{\pi }} \hspace{0.15 cm}\underline{= {\rm{0}}{\rm{.636}} | + | :*Bei der Frequenz $f = 0$ hat auch ${y(t)}$ keine Spektralanteile ⇒ ${Y(f = 0)} \;\underline{= 0}$. |
| + | :*Für $f = 1\,\text{kHz} \ \ (f \cdot T = 0.5)$ erhält man gegenüber $X(f)$ einen um den Faktor $\pi$ kleineren Wert: | ||
| + | :$$|Y( {f = 1\;{\rm{kHz}}} )| = \frac{4 \cdot A \cdot T}{\rm{\pi }} \hspace{0.15 cm}\underline{= {\rm{0}}{\rm{.636}} \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 27. April 2021, 13:27 Uhr
Wie in der Aufgabe 3.5 soll das Spektrum ${Y(f)}$ des Signals
- $$y( t ) = \left\{ \begin{array}{c} A \\ - A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {{\rm{f \ddot{u}r}}} \\ {{\rm{f\ddot{u} r}}} \\ {\rm{sonst.}} \\ \end{array}\;\begin{array}{*{20}c} { - T \le t < 0,} \\ {0 < t \le T,} \\ {} \\\end{array}$$
ermittelt werden. Es gelte wieder $A = 1 \,\text{V}$ und $T = 0.5 \,\text{ms}$.
Ausgegangen wird vom Zeitsignal ${x(t)}$ gemäß der mittleren Skizze, das sich aus drei Diracimpulsen bei $–T$, $0$ und $+T$ mit den Impulsgewichte ${AT}$, $-2{AT}$ und ${AT}$ zusammensetzt.
Die Spektralfunktion ${X(f)}$ kann durch Anwendung des Vertauschungssatzes direkt angegeben werden, wenn man berücksichtigt, dass die zu ${U(f)}$ gehörige Zeitfunktion wie folgt lautet (siehe untere Skizze):
- $$u( t ) = - 2A + 2A \cdot \cos ( {2{\rm{\pi }}f_0 t} ).$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Gesetzmäßigkeiten der Fouriertransformation.
- Alle diese Gesetzmäßigkeiten werden im Lernvideo Gesetzmäßigkeiten der Fouriertransformation an Beispielen verdeutlicht.
- Zwischen ${x(t)}$ und ${y(t)}$ besteht folgender Zusammenhang:
- $$y( t ) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )}\, {\rm d}\tau .$$
- Der Integrationssatz lautet in entsprechend angepasster Form:
- $$\frac{1}{T}\cdot \hspace{-0.1cm} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )}\,\, {\rm d}\tau\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ X( f ) \cdot \left( {\frac{1}{{{\rm{j}}\cdot 2{\rm{\pi }\cdot }fT}} + \frac{1}{2T}\cdot {\rm \delta} ( f )} \right).$$
Fragebogen
Musterlösung
(1) Im Angabenteil zur Aufgabe finden Sie die Fourierkorrespondenz zwischen ${u(t)}$ und ${U(f)}$.
- Da sowohl die Zeitfunktionen ${u(t)}$ und ${x(t)}$ als auch die dazugehörigen Spektren ${U(f)}$ und ${X(f)}$ gerade und reell sind, kann man ${X(f)}$ durch Anwendung des Vertauschungssatzes leicht berechnen:
- $$X( f ) = - 2 \cdot A \cdot T + 2 \cdot A \cdot T \cdot \cos \left( {{\rm{2\pi }}fT} \right).$$
- Wegen der Beziehung $\sin^{2}(\alpha) = (1 – \cos(\alpha))/2$ kann hierfür auch geschrieben werden:
- $$X( f ) = - 4 \cdot A \cdot T \cdot \sin ^2 ( {{\rm{\pi }}fT} ).$$
- Bei der Frequenz $f = 0$ hat ${x(t)}$ keine Spektralanteile ⇒ ${X(f = 0)} \;\underline{= 0}$.
- Für $f = 1 \,\text{kHz}$ – also $f \cdot T = 0.5$ – gilt dagegen:
- $$X( f = 1\;{\rm{kHz}} ) = - 4 \cdot A \cdot T = -2 \cdot 10^{ - 3} \;{\rm{V/Hz}}\; \Rightarrow \; |X( {f = 1\;{\rm{kHz}}} )| \hspace{0.15 cm}\underline{= 2 \;{\rm{mV/Hz}}}{\rm{.}}$$
(2) Das Spektrum ${Y(f)}$ kann aus ${X(f)}$ durch Anwendung des Integrationssatzes ermittelt werden.
- Wegen ${X(f = 0)} = 0$ muss die Diracfunktion bei der Frequenz $f = 0$ nicht berücksichtigt werden und man erhält:
- $$Y( f ) = \frac{X( f )}{{{\rm{j}} \cdot 2{\rm{\pi }}fT}} = \frac{{ - 4 \cdot A \cdot T \cdot \sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{j}}\cdot 2{\rm{\pi }}fT}} = 2{\rm{j}} \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$
- Es ergibt sich selbstverständlich das gleiche Ergebnis wie in der Aufgabe 3.5:
- Bei der Frequenz $f = 0$ hat auch ${y(t)}$ keine Spektralanteile ⇒ ${Y(f = 0)} \;\underline{= 0}$.
- Für $f = 1\,\text{kHz} \ \ (f \cdot T = 0.5)$ erhält man gegenüber $X(f)$ einen um den Faktor $\pi$ kleineren Wert:
- $$|Y( {f = 1\;{\rm{kHz}}} )| = \frac{4 \cdot A \cdot T}{\rm{\pi }} \hspace{0.15 cm}\underline{= {\rm{0}}{\rm{.636}} \;{\rm{mV/Hz}}}{\rm{.}}$$