Aufgaben:Aufgabe 4.13: Gaußförmige AKF: Unterschied zwischen den Versionen
| Zeile 76: | Zeile 76: | ||
:$$K\cdot{\rm e}^{-\pi({\tau}/{\nabla\tau_x})^2}\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \frac{\it K}{\nabla \it f_x}\cdot{\rm e}^{-\pi({f}/{\nabla f_x})^2}.$$ | :$$K\cdot{\rm e}^{-\pi({\tau}/{\nabla\tau_x})^2}\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \frac{\it K}{\nabla \it f_x}\cdot{\rm e}^{-\pi({f}/{\nabla f_x})^2}.$$ | ||
| − | Mit $K = 0.25 \hspace{0.05cm}\rm V^2$ und $ {\rm \nabla} \hspace{-0.05cm} f_x = 200\hspace{0.05cm} \rm kHz$ erhält man: | + | *Mit $K = 0.25 \hspace{0.05cm}\rm V^2$ und $ {\rm \nabla} \hspace{-0.05cm} f_x = 200\hspace{0.05cm} \rm kHz$ erhält man: |
:$${\it \Phi_x}(f)=1.25\cdot\rm 10^{-\rm 6}\hspace{0.1cm}\frac{V^2}{Hz}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_x})^2}\hspace{0.3cm} | :$${\it \Phi_x}(f)=1.25\cdot\rm 10^{-\rm 6}\hspace{0.1cm}\frac{V^2}{Hz}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_x})^2}\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}{\it \Phi_x}(f = 0)=\hspace{0.15cm}\underline{\rm 1.25 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}, | \Rightarrow \hspace{0.3cm}{\it \Phi_x}(f = 0)=\hspace{0.15cm}\underline{\rm 1.25 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}, | ||
| Zeile 83: | Zeile 83: | ||
'''(3)''' Richtig sind die <u>Lösungsvorschläge 1, 2 und 4</u>: | '''(3)''' Richtig sind die <u>Lösungsvorschläge 1, 2 und 4</u>: | ||
| − | *Ein mittelwertfreier Prozess hat stets ein kontinuierliches LDS zur Folge. Dieses ist um so schmaler, je breiter die AKF ist (Reziprozitätsgesetz). | + | *Ein mittelwertfreier Prozess hat stets ein kontinuierliches LDS zur Folge. Dieses ist um so schmaler, je breiter die AKF ist (Reziprozitätsgesetz). |
| − | * | + | *Die Prozessleistung ist gleich dem Integral über das LDS. |
| − | *Deshalb muss bei konstanter Leistung eine breitere AKF (schmaleres LDS) durch höhere LDS-Werte ausgeglichen werden. | + | *Deshalb muss bei konstanter Leistung eine breitere AKF (schmaleres LDS) durch höhere LDS-Werte ausgeglichen werden. |
| − | *Ein Gleichanteil oder periodische Anteile führen stets zu Diracfunktionen im LDS; ansonsten ist das LDS stets wertkontinuierlich. | + | *Ein Gleichanteil oder periodische Anteile führen stets zu Diracfunktionen im LDS; ansonsten ist das LDS stets wertkontinuierlich. |
| − | '''(4)''' Analog zu Teilaufgabe '''(2)''' gilt mit $ {\rm \nabla} \hspace{-0.05cm} f_y = 100\hspace{0.05cm} \rm kHz$: | + | |
| + | '''(4)''' Analog zu Teilaufgabe '''(2)''' gilt mit $ {\rm \nabla} \hspace{-0.05cm} f_y = 100\hspace{0.05cm} \rm kHz$: | ||
:$${\it \Phi_y}(f)=\frac{\rm 0.09 V^2}{\nabla\it f_y}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_y})^2}+\it m_y^{\rm 2}\cdot\delta(f).$$ | :$${\it \Phi_y}(f)=\frac{\rm 0.09 V^2}{\nabla\it f_y}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_y})^2}+\it m_y^{\rm 2}\cdot\delta(f).$$ | ||
*Aufgrund des Gleichanteils gibt es zusätzlich zum kontinuierlichen LDS-Anteil noch einen Dirac bei der Frequenz $f = 0$. | *Aufgrund des Gleichanteils gibt es zusätzlich zum kontinuierlichen LDS-Anteil noch einen Dirac bei der Frequenz $f = 0$. | ||
| − | *Der kontinuierliche LDS–Anteil bei $f= 0$ beträgt ${\it \Phi_y}(f = 0)=\hspace{0.15cm}\underline{\rm 0.9 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$ | + | *Der kontinuierliche LDS–Anteil bei $f= 0$ beträgt ${\it \Phi_y}(f = 0)=\hspace{0.15cm}\underline{\rm 0.9 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$ |
| − | *Der Anteil bei $f = 2 \cdot {\rm \nabla} \hspace{-0.05cm} f_y = 200 \hspace{0.05cm}\rm kHz$ ist um den Faktor ${\rm e}^{-4} \approx 0.0183$ geringer ⇒ ${\it \Phi_y}(f )=\hspace{0.15cm}\underline{\rm 0.0165 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$ | + | *Der Anteil bei $f = 2 \cdot {\rm \nabla} \hspace{-0.05cm} f_y = 200 \hspace{0.05cm}\rm kHz$ ist um den Faktor ${\rm e}^{-4} \approx 0.0183$ geringer ⇒ ${\it \Phi_y}(f )=\hspace{0.15cm}\underline{\rm 0.0165 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$ |
'''(5)''' Richtig ist <u>nur der zweite Lösungsvorschlag</u>: | '''(5)''' Richtig ist <u>nur der zweite Lösungsvorschlag</u>: | ||
| − | *Das LDS eines mittelwertbehafteten Prozesses beinhaltet allgemein eine Diracfunktion bei $f=0$ mit Gewicht $m_y^2$. | + | *Das LDS eines mittelwertbehafteten Prozesses beinhaltet allgemein eine Diracfunktion bei $f=0$ mit Gewicht $m_y^2$. |
| − | * Im vorliegenden Fall ist dieser Wert gleich $0.16 \ \rm V^2$. | + | * Im vorliegenden Fall ist dieser Wert gleich $0.16 \ \rm V^2$. |
| − | *Da $\delta(f)$ die Einheit $\rm 1/Hz = s$ besitzt, unterscheiden sich die Einheiten des kontinuierlichen und des diskreten LDS-Anteils. | + | *Da $\delta(f)$ die Einheit $\rm 1/Hz = s$ besitzt, unterscheiden sich die Einheiten des kontinuierlichen und des diskreten LDS-Anteils. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 2. Dezember 2019, 12:06 Uhr
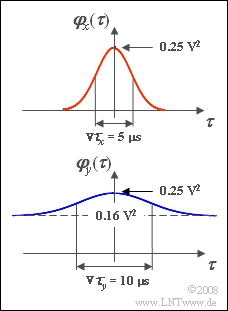
Der hier betrachtete Zufallsprozess $\{x_i(t)\}$ sei durch die oben skizzierte Autokorrelationsfunktion (AKF) charakterisiert. Dieser Zufallsprozess ist mittelwertfrei und die äquivalente AKF-Dauer beträgt ${ {\rm \nabla} }\tau_x = 5 \hspace{0.08cm} \rm µ s$:
- $$\varphi_x(\tau)=\rm 0.25 V^2\cdot \rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}{/ 5 \hspace{0.08cm}{\rm µ}s })^2} .$$
Im unteren Bild ist die AKF des Prozesses $\{y_i(t)\}$ dargestellt. Diese lautet mit der äquivalenten AKF-Dauer ${ {\rm \nabla} }\tau_y = 10 \hspace{0.08cm} \rm µ s$:
- $$ \varphi_y(\tau)=\rm 0.16 V^2 + \rm 0.09 V^2\cdot\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}/{\nabla \it \tau_y})^2} .$$
In dieser Aufgabe werden die Leistungsdichtespektren der beiden Prozesse gesucht.
Hinweise:
- Die Aufgabe gehört zum Kapitel Leistungsdichtespektrum.
- Bezug genommen wird auch auf das Kapitel Autokorrelationsfunktion.
- Zur Lösung dieser Aufgabe können Sie die folgende Fourierkorrespondenz benutzen:
- $$\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\it f}/{\rm \Delta\it f})^2}\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \ {\rm \Delta \it f} \cdot \rm e^{-\pi \hspace{0.05cm}\cdot \hspace{0.05cm} ({\rm \Delta\it f} \hspace{0.05cm}\cdot \hspace{0.05cm}\it t {\rm )}^{\rm 2}}.$$
Fragebogen
Musterlösung
- $$\nabla f_x = 1 / \nabla \tau_x \hspace{0.15cm}\underline{= {\rm 200\hspace{0.1cm}kHz}}.$$
(2) Die angegebene Fourierkorrespondenz kann man wie folgt an die Aufgabenstellung anpassen:
- $$K\cdot{\rm e}^{-\pi({\tau}/{\nabla\tau_x})^2}\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \frac{\it K}{\nabla \it f_x}\cdot{\rm e}^{-\pi({f}/{\nabla f_x})^2}.$$
- Mit $K = 0.25 \hspace{0.05cm}\rm V^2$ und $ {\rm \nabla} \hspace{-0.05cm} f_x = 200\hspace{0.05cm} \rm kHz$ erhält man:
- $${\it \Phi_x}(f)=1.25\cdot\rm 10^{-\rm 6}\hspace{0.1cm}\frac{V^2}{Hz}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_x})^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\it \Phi_x}(f = 0)=\hspace{0.15cm}\underline{\rm 1.25 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}, \hspace{0.5cm}{\it \Phi_x}(f = 200 \hspace{0.05cm} \rm kHz)=\hspace{0.15cm}\underline{\rm 0.054 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$$
(3) Richtig sind die Lösungsvorschläge 1, 2 und 4:
- Ein mittelwertfreier Prozess hat stets ein kontinuierliches LDS zur Folge. Dieses ist um so schmaler, je breiter die AKF ist (Reziprozitätsgesetz).
- Die Prozessleistung ist gleich dem Integral über das LDS.
- Deshalb muss bei konstanter Leistung eine breitere AKF (schmaleres LDS) durch höhere LDS-Werte ausgeglichen werden.
- Ein Gleichanteil oder periodische Anteile führen stets zu Diracfunktionen im LDS; ansonsten ist das LDS stets wertkontinuierlich.
(4) Analog zu Teilaufgabe (2) gilt mit $ {\rm \nabla} \hspace{-0.05cm} f_y = 100\hspace{0.05cm} \rm kHz$:
- $${\it \Phi_y}(f)=\frac{\rm 0.09 V^2}{\nabla\it f_y}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_y})^2}+\it m_y^{\rm 2}\cdot\delta(f).$$
- Aufgrund des Gleichanteils gibt es zusätzlich zum kontinuierlichen LDS-Anteil noch einen Dirac bei der Frequenz $f = 0$.
- Der kontinuierliche LDS–Anteil bei $f= 0$ beträgt ${\it \Phi_y}(f = 0)=\hspace{0.15cm}\underline{\rm 0.9 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$
- Der Anteil bei $f = 2 \cdot {\rm \nabla} \hspace{-0.05cm} f_y = 200 \hspace{0.05cm}\rm kHz$ ist um den Faktor ${\rm e}^{-4} \approx 0.0183$ geringer ⇒ ${\it \Phi_y}(f )=\hspace{0.15cm}\underline{\rm 0.0165 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$
(5) Richtig ist nur der zweite Lösungsvorschlag:
- Das LDS eines mittelwertbehafteten Prozesses beinhaltet allgemein eine Diracfunktion bei $f=0$ mit Gewicht $m_y^2$.
- Im vorliegenden Fall ist dieser Wert gleich $0.16 \ \rm V^2$.
- Da $\delta(f)$ die Einheit $\rm 1/Hz = s$ besitzt, unterscheiden sich die Einheiten des kontinuierlichen und des diskreten LDS-Anteils.