Aufgaben:Aufgabe 2.8: COST-Verzögerungsmodelle: Unterschied zwischen den Versionen
| Zeile 100: | Zeile 100: | ||
Hierbei bezeichnet $\tau_{-30}$ die Verzögerungszeit, die zum logarithmischen Ordinatenwert $-30 \ \rm dB$ führt. Damit erhält man | Hierbei bezeichnet $\tau_{-30}$ die Verzögerungszeit, die zum logarithmischen Ordinatenwert $-30 \ \rm dB$ führt. Damit erhält man | ||
| − | * für ländliches Gebiet (<i>Rural Area</i>, <b>RA</b>) mit $\tau_{–30} = 0.75 \ \rm | + | * für ländliches Gebiet (<i>Rural Area</i>, <b>RA</b>) mit $\tau_{–30} = 0.75 \ \rm µ s$: |
| − | :$$\tau_{\rm 0} = \frac{0.75\,{\rm \mu s}}{ 6.9} \hspace{0.1cm}\underline {\approx 0.109\,{\rm | + | :$$\tau_{\rm 0} = \frac{0.75\,{\rm \mu s}}{ 6.9} \hspace{0.1cm}\underline {\approx 0.109\,{\rm µ s}} |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * für Städte und Vorote (<i>Typical Urban</i>, <b>TU</b>) mit $\tau_{–30} = 6.9 \ \rm | + | * für Städte und Vorote (<i>Typical Urban</i>, <b>TU</b>) mit $\tau_{–30} = 6.9 \ \rm µ s$: |
| − | :$$\tau_{\rm 0} = \frac{6.9\,{\rm \mu s}}{ 6.9} \hspace{0.1cm}\underline {\approx 1\,{\rm | + | :$$\tau_{\rm 0} = \frac{6.9\,{\rm \mu s}}{ 6.9} \hspace{0.1cm}\underline {\approx 1\,{\rm µ s}} |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
'''(2)''' In der [[Aufgaben:2.7_Koh%C3%A4renzbandbreite| Aufgabe 2.7]] wurde gezeigt, dass die Mehrwegeverbreitung $T_{\rm V} =\tau_0$ ist, wenn das Verzögerungs–Leistungsdichtespektrum entsprechend ${\rm e}^{-\tau/\tau_0}$ exponentiell abfällt. Es gilt demnach | '''(2)''' In der [[Aufgaben:2.7_Koh%C3%A4renzbandbreite| Aufgabe 2.7]] wurde gezeigt, dass die Mehrwegeverbreitung $T_{\rm V} =\tau_0$ ist, wenn das Verzögerungs–Leistungsdichtespektrum entsprechend ${\rm e}^{-\tau/\tau_0}$ exponentiell abfällt. Es gilt demnach | ||
| − | * für „Rural Area”: $\hspace{0.4cm} T_{\rm V} \ \underline {= 0.109 \ \rm | + | * für „Rural Area”: $\hspace{0.4cm} T_{\rm V} \ \underline {= 0.109 \ \rm µ s}$, |
| − | * für „Typical Urban”: $\hspace{0.4cm} T_{\rm V} \ \underline {= 1 \ \rm \ | + | * für „Typical Urban”: $\hspace{0.4cm} T_{\rm V} \ \underline {= 1 \ \rm µ s}$. |
| + | |||
| + | |||
| + | |||
| + | '''(3)''' In der [[Aufgaben:2.7_Koh%C3%A4renzbandbreite| Aufgabe A2.7]] wurde auch gezeigt, dass für die Kohärenzbandbreite $B_{\rm K} \approx 0.276/\tau_0$ gilt. Daraus folgt: | ||
| + | *$B_{\rm K} \ \underline {\approx 2500 \ \rm kHz}$ („Rural Area”), | ||
| + | * $B_{\rm K} \ \underline {\approx 276 \ \rm kHz}$ („Typical Union”). | ||
| − | |||
| Zeile 121: | Zeile 126: | ||
| − | '''(5)''' Entsprechend der angegebenen Gleichung ist ${\it \Phi}_{\rm V}(\tau = 5.001 \ \rm | + | |
| − | :$${{\it \Phi}_{\rm V}(\tau = 4.999\,{\rm \mu s})}/{{\it \Phi}_{\rm 0}} = {\rm e}^{ -{4.999\,{\rm | + | '''(5)''' Entsprechend der angegebenen Gleichung ist ${\it \Phi}_{\rm V}(\tau = 5.001 \ \rm µ s)/{\it \Phi}_0 \hspace{0.15cm}\underline{\approx0.5}$. |
| + | *Dagegen gilt für geringfügig kleineres $\tau$ (zum Beispiel $\tau = 4.999 \ \rm µ s$) mit guter Näherung: | ||
| + | :$${{\it \Phi}_{\rm V}(\tau = 4.999\,{\rm \mu s})}/{{\it \Phi}_{\rm 0}} = {\rm e}^{ -{4.999\,{\rm µ s}}/{ 1\,{\rm \mu s}}} | ||
\approx {\rm e}^{-5} \hspace{0.1cm}\underline {= 0.00674 }\hspace{0.05cm}.$$ | \approx {\rm e}^{-5} \hspace{0.1cm}\underline {= 0.00674 }\hspace{0.05cm}.$$ | ||
| − | '''(6)''' Für die Leistung $P_1$ aller Signalanteile mit Verzögerungszeiten zwischen $0$ und $5 \ \rm | + | '''(6)''' Für die Leistung $P_1$ aller Signalanteile mit Verzögerungszeiten zwischen $0$ und $5 \ \rm s$ gilt: |
:$$P_1 = {\it \Phi}_{\rm 0} \cdot \int_{0}^{5\,{\rm \mu s}} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} | :$$P_1 = {\it \Phi}_{\rm 0} \cdot \int_{0}^{5\,{\rm \mu s}} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} | ||
{\it \Phi}_{\rm 0} \cdot \int_{0}^{\infty} {\rm e}^{ -{\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau | {\it \Phi}_{\rm 0} \cdot \int_{0}^{\infty} {\rm e}^{ -{\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau | ||
= {\it \Phi}_{\rm 0} \cdot \tau_0 \hspace{0.05cm}.$$ | = {\it \Phi}_{\rm 0} \cdot \tau_0 \hspace{0.05cm}.$$ | ||
| − | Für den zweiten Anteil erhält man: | + | *Für den zweiten Anteil erhält man: |
| − | :$$P_2 = \frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{5\,{\rm | + | :$$P_2 = \frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{5\,{\rm µ s}}^{\infty} {\rm exp}[ \frac{5\,{\rm µ s} -\tau}{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} |
\frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{0}^{\infty} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau | \frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{0}^{\infty} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau | ||
= \frac{{\it \Phi}_{\rm 0} \cdot \tau_0}{2} \hspace{0.05cm}. $$ | = \frac{{\it \Phi}_{\rm 0} \cdot \tau_0}{2} \hspace{0.05cm}. $$ | ||
| − | + | *Entsprechend beträgt der prozentuale Anteil des ersten Anteils: | |
| + | [[Datei:P_ID2184__Mob_A_2_8f.png|right|frame|Verzögerungs–Leistungsdichte der COST–Profile ${\rm BU}$ und ${\rm HT}$]] | ||
:$$\frac{P_1}{P_1+ P_2} = \frac{2}{3} \hspace{0.15cm}\underline {\approx 66.7\%}\hspace{0.05cm}.$$ | :$$\frac{P_1}{P_1+ P_2} = \frac{2}{3} \hspace{0.15cm}\underline {\approx 66.7\%}\hspace{0.05cm}.$$ | ||
| − | + | ||
Die Grafik zeigt ${\it \Phi}_{\rm V}(\tau)$ in linearem Maßstab: | Die Grafik zeigt ${\it \Phi}_{\rm V}(\tau)$ in linearem Maßstab: | ||
*Eingezeichnet sind die Flächen $P_1$ und $P_2$. | *Eingezeichnet sind die Flächen $P_1$ und $P_2$. | ||
| − | *Die linke Abbildung gilt für & | + | *Die linke Abbildung gilt für ${\rm BU}$, die rechte für ${\rm HT}$. |
| − | *Bei Letzterem beträgt der Leistungsanteil aller späteren Echos (später als $15 \ \rm | + | *Bei Letzterem beträgt der Leistungsanteil aller späteren Echos (später als $15 \ \rm µ s$) nur etwa $12\%$. |
<br clear=all> | <br clear=all> | ||
| − | '''(7)''' Die Fläche über das gesamte Leistungsdichtespektrum ergibt $P = 1.5 \cdot \phi_0 \cdot \tau_0$. Normiert man ${\it \Phi}_{\rm V}(\tau)$ auf diesen Wert, so erhält man die Wahrscheinlichkeitsdichtefunktion $f_{\rm V}(\tau)$, wie in der nächsten Grafik dargestellt (linkes Diagramm). | + | '''(7)''' Die Fläche über das gesamte Leistungsdichtespektrum ergibt $P = 1.5 \cdot \phi_0 \cdot \tau_0$. |
| + | *Normiert man ${\it \Phi}_{\rm V}(\tau)$ auf diesen Wert, so erhält man die Wahrscheinlichkeitsdichtefunktion $f_{\rm V}(\tau)$, wie in der nächsten Grafik dargestellt (linkes Diagramm). | ||
| − | [[Datei:P_ID2185__Mob_A_2_8g.png|right|frame|Verzögerungs–WDF des Profils | + | [[Datei:P_ID2185__Mob_A_2_8g.png|right|frame|Verzögerungs–WDF des Profils ${\rm BU}$]] |
| − | Mit $\tau_0 = 1 \ \rm | + | *Mit $\tau_0 = 1 \ \rm µ s$, $\tau_5 = 5 \ \rm µ s$ ergibt sich für den linearen Mittelwert: |
:$$m_{\rm V}= \int_{0}^{\infty} f_{\rm V}(\tau) \hspace{0.15cm}{\rm d} \tau$$ | :$$m_{\rm V}= \int_{0}^{\infty} f_{\rm V}(\tau) \hspace{0.15cm}{\rm d} \tau$$ | ||
:$$\Rightarrow \hspace{0.3cm}m_{\rm V}= \frac{2}{3\tau_0} \cdot \int_{0}^{\tau_5} \tau \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau \ + $$ | :$$\Rightarrow \hspace{0.3cm}m_{\rm V}= \frac{2}{3\tau_0} \cdot \int_{0}^{\tau_5} \tau \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau \ + $$ | ||
:$$ \hspace{1.7cm}+\ \frac{1}{3\tau_0} \cdot \int_{\tau_5}^{\infty} \tau \cdot {\rm e}^{ (\tau_5 -\tau)/\tau_0}\hspace{0.15cm}{\rm d} \tau \hspace{0.05cm}. $$ | :$$ \hspace{1.7cm}+\ \frac{1}{3\tau_0} \cdot \int_{\tau_5}^{\infty} \tau \cdot {\rm e}^{ (\tau_5 -\tau)/\tau_0}\hspace{0.15cm}{\rm d} \tau \hspace{0.05cm}. $$ | ||
| − | Das erste Interal ist nach der angegebenen Gleichung gleich $2\tau_0/3$. | + | *Das erste Interal ist nach der angegebenen Gleichung gleich $2\tau_0/3$. |
| − | Mit der Substitution $\tau' = \tau \, -\tau_5$ erhält man schließlich unter Verwendung der vorne angegebenen Integrallösungen: | + | *Mit der Substitution $\tau' = \tau \, -\tau_5$ erhält man schließlich unter Verwendung der vorne angegebenen Integrallösungen: |
:$$m_{\rm V} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{2\tau_0}{3} + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau') \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' = \frac{2\tau_0}{3} + | :$$m_{\rm V} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{2\tau_0}{3} + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau') \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' = \frac{2\tau_0}{3} + | ||
\frac{\tau_5}{3\tau_0} \cdot \int_{0}^{\infty} \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' + | \frac{\tau_5}{3\tau_0} \cdot \int_{0}^{\infty} \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' + | ||
\frac{1}{3\tau_0} \cdot \int_{0}^{\infty} \tau' \cdot \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' $$ | \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} \tau' \cdot \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' $$ | ||
:$$\Rightarrow \hspace{0.3cm}m_{\rm V}= \frac{2\tau_0}{3} + \frac{\tau_5}{3}+ \frac{\tau_0}{3} = \tau_0 + \frac{\tau_5}{3} | :$$\Rightarrow \hspace{0.3cm}m_{\rm V}= \frac{2\tau_0}{3} + \frac{\tau_5}{3}+ \frac{\tau_0}{3} = \tau_0 + \frac{\tau_5}{3} | ||
| − | \hspace{0.15cm}\underline {\approx 2.667\,{\rm | + | \hspace{0.15cm}\underline {\approx 2.667\,{\rm µ s}} |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | Die Varianz $\sigma_{\rm V}^2$ ist gleich dem quadratischen Mittelwert der mittelwertbefreiten Zufallsgröße $\theta = \tau \, –m_{\rm V}$, deren WDF in der rechten Grafik dargestellt ist. Daraus lässt sich $T_{\rm V} = \sigma_{\rm V}$ angeben. | + | *Die Varianz $\sigma_{\rm V}^2$ ist gleich dem quadratischen Mittelwert der mittelwertbefreiten Zufallsgröße $\theta = \tau \, –m_{\rm V}$, deren WDF in der rechten Grafik dargestellt ist. |
| + | *Daraus lässt sich $T_{\rm V} = \sigma_{\rm V}$ angeben. | ||
| − | Eine zweite Möglichkeit besteht darin, zunächst den quadratischen Mittelwert der Zufallsgröße $\tau$ zu berechnen und daraus die Varianz $\sigma_{\rm V}^2$ mit dem Satz von Steiner. Mit den bereits oben beschriebenen Substitutionen und Näherungen erhält man so: | + | *Eine zweite Möglichkeit besteht darin, zunächst den quadratischen Mittelwert der Zufallsgröße $\tau$ zu berechnen und daraus die Varianz $\sigma_{\rm V}^2$ mit dem Satz von Steiner. |
| + | *Mit den bereits oben beschriebenen Substitutionen und Näherungen erhält man so: | ||
:$$m_{\rm V2} \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} \frac{2}{3\tau_0} \cdot \int_{0}^{\infty} \tau^2 \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau')^2 \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' $$ | :$$m_{\rm V2} \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} \frac{2}{3\tau_0} \cdot \int_{0}^{\infty} \tau^2 \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau')^2 \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' $$ | ||
:$$\Rightarrow \hspace{0.3cm}m_{\rm V2} = \frac{2}{3} \cdot \int_{0}^{\infty} \frac{\tau^2}{\tau_0} \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau + \frac{\tau_5^2}{3} \cdot \int_{0}^{\infty} \frac{1}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' +\frac{2\tau_5}{3} \cdot \int_{0}^{\infty} \frac{\tau '}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' + \frac{1}{3} \cdot \int_{0}^{\infty} \frac{{\tau '}^2}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' | :$$\Rightarrow \hspace{0.3cm}m_{\rm V2} = \frac{2}{3} \cdot \int_{0}^{\infty} \frac{\tau^2}{\tau_0} \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau + \frac{\tau_5^2}{3} \cdot \int_{0}^{\infty} \frac{1}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' +\frac{2\tau_5}{3} \cdot \int_{0}^{\infty} \frac{\tau '}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' + \frac{1}{3} \cdot \int_{0}^{\infty} \frac{{\tau '}^2}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | Mit den vorne angegebenen Integralen folgt daraus: | + | *Mit den vorne angegebenen Integralen folgt daraus: |
:$$m_{\rm V2} \approx \frac{2}{3} \cdot 2 \tau_0^2 + \frac{\tau_5^2}{3} \cdot 1 + \frac{2\tau_5}{3} \cdot \tau_0 + | :$$m_{\rm V2} \approx \frac{2}{3} \cdot 2 \tau_0^2 + \frac{\tau_5^2}{3} \cdot 1 + \frac{2\tau_5}{3} \cdot \tau_0 + | ||
\frac{1}{3} \cdot 2 \tau_0^2 = 2 \tau_0^2 + \frac{\tau_5^2}{3} + \frac{2 \cdot \tau_0 \cdot \tau_5}{3} $$ | \frac{1}{3} \cdot 2 \tau_0^2 = 2 \tau_0^2 + \frac{\tau_5^2}{3} + \frac{2 \cdot \tau_0 \cdot \tau_5}{3} $$ | ||
:$$\Rightarrow \hspace{0.3cm} \sigma_{\rm V}^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} m_{\rm V2} - m_{\rm V}^2 = 2 \tau_0^2 + \frac{\tau_5^2}{3} + \frac{2 \cdot \tau_0 \cdot \tau_5}{3} | :$$\Rightarrow \hspace{0.3cm} \sigma_{\rm V}^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} m_{\rm V2} - m_{\rm V}^2 = 2 \tau_0^2 + \frac{\tau_5^2}{3} + \frac{2 \cdot \tau_0 \cdot \tau_5}{3} | ||
| − | - (\tau_0 + \frac{\tau_5}{3})^2 =\tau_0^2 + \frac{2\tau_5^2}{9} = (1\,{\rm | + | - (\tau_0 + \frac{\tau_5}{3})^2 =\tau_0^2 + \frac{2\tau_5^2}{9} = (1\,{\rm µ s})^2 + \frac{2\cdot (5\,{\rm µ s})^2}{9} = 6.55\,({\rm µ s})^2$$ |
| − | :$$\Rightarrow \hspace{0.3cm} T_{\rm V} = \sigma_{\rm V} \hspace{0.15cm}\underline {\approx 2.56\,{\rm | + | :$$\Rightarrow \hspace{0.3cm} T_{\rm V} = \sigma_{\rm V} \hspace{0.15cm}\underline {\approx 2.56\,{\rm µ s}}\hspace{0.05cm}.$$ |
In obiger Grafik sind die Kenngrößen $T_{\rm V}$ und $\sigma_{\rm V}$ eingezeichnet. | In obiger Grafik sind die Kenngrößen $T_{\rm V}$ und $\sigma_{\rm V}$ eingezeichnet. | ||
Version vom 14. April 2019, 12:36 Uhr
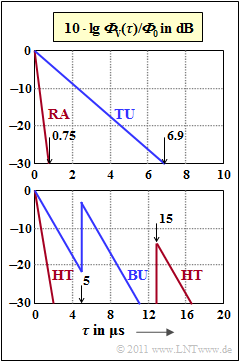
Rechts sind vier Verzögerungs–Leistungsdichtespektren als Funktion der Verzögerungszeit $\tau$ logarithmisch aufgetragen:
- $$10 \cdot {\rm lg}\hspace{0.15cm} ({{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0}) \hspace{0.05cm},$$
Hierbei ist als Abkürzung $\phi_0 = \phi_{\rm V}(\tau = 0)$ verwendet. Es handelt sich um die so genannten COST–Verzögerungsmodelle.
Die obere Skizze beinhaltet die beiden Profile ${\rm RA}$ (Rural Area) und ${\rm TU}$ (Typical Urban). Für diese gilt folgender Verlauf:
- $${{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.05cm}.$$
Der Wert des Parameters $\tau_0$ (Zeitkonstante der AKF) soll in der Teilaufgabe (1) aus der Grafik ermittelt werden. Beachten Sie hierzu die angegebenen $\tau$–Werte für $-30 \ \rm dB$:
- $${\rm RA}\text{:}\hspace{0.15cm}\tau_{-30} = 0.75\,{\rm µ s} \hspace{0.05cm},\hspace{0.2cm} {\rm TU}\text{:}\hspace{0.15cm}\tau_{-30} = 6.9\,{\rm µ s} \hspace{0.05cm}. $$
Die untere Grafik gilt für ungünstigere Verhältnisse in
- städtischen Gebieten (Bad Urban, ${\rm BU}$):
- $${{\it \Phi}_{\rm V}(\tau)}/{{\it \Phi}_{\rm 0}} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0} \\ 0.5 \cdot {\rm e}^{ (5\,{\rm \mu s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.55cm} {\rm Bereich}\hspace{0.15cm}0 < \tau < 5\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}, \\ \hspace{-0.15cm} {\,\, \,\, \rm Bereich}\hspace{0.15cm}5\,{\rm µ s} < \tau < 10\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}, \end{array}$$
- in ländlichen Gebieten (Hilly Terrain, ${\rm HT}$):
- $${{\it \Phi}_{\rm V}(\tau)}/{{\it \Phi}_{\rm 0}} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0} \\ {0.04 \cdot \rm e}^{ (15\,{\rm \mu s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.55cm} {\rm Bereich}\hspace{0.15cm}0 < \tau < 2\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.286\,{\rm µ s} \hspace{0.05cm}, \\ \hspace{-0.35cm} {\rm Bereich}\hspace{0.15cm}15\,{\rm µ s} < \tau < 20\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \end{array}$$
Für die Modelle ${\rm RA}$, ${\rm TU}$ und ${\rm BU}$ sollen folgende Kenngrößen ermittelt werden:
- Die Mehrwegeverbreiterung $T_{\rm V}$ ist die Standardabweichung der Verzögerungszeit $\tau$.
Hat das Verzögerungs–LDS ${\it \Phi}_{\rm V}(\tau)$ einen exponentiellen Verlauf wie bei den Profilen ${\rm RA}$ und ${\rm TU}$, so gilt $T_{\rm V} = \tau_0$, siehe Aufgabe 2.7.
- Die Kohärenzbandbreite $B_{\rm K}$ ist der $\Delta f$–Wert, bei dem die Frequenz–Korrelationsfunktion $\varphi_{\rm F}(\Delta f)$ betragsmäßig erstmals auf die Hälfte abgefallen ist.
Bei exponentiellem ${\it \Phi}_{\rm V}(\tau)$ wie bei ${\rm RA}$ und ${\rm TU}$ ist das Produkt $T_{\rm V} \cdot B_{\rm K} \approx 0.276$, siehe Aufgabe 2.7.
Hinweise:
- Die Aufgabe gehört zum Kapitel GWSSUS–Kanalmodell.
- Vorgegeben sind die folgenden Integrale:
- $$\frac{1}{\tau_0} \cdot \int_{0}^{\infty}\hspace{-0.15cm} {\rm e}^{ -\tau / \tau_0} \hspace{0.15cm}{\rm d} \tau = 1 \hspace{0.05cm},\hspace{0.6cm} \frac{1}{\tau_0} \cdot \int_{0}^{\infty}\hspace{-0.15cm} {\tau} \cdot{\rm e}^{ -\tau / \tau_0}\hspace{0.15cm}{\rm d} \tau = \tau_0 \hspace{0.05cm},\hspace{0.6cm} \frac{1}{\tau_0} \cdot \int_{0}^{\infty} \hspace{-0.15cm}{\tau^2} \cdot{\rm e}^{ -\tau / \tau_0}\hspace{0.15cm}{\rm d} \tau = 2\tau_0^2\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$10 \cdot {\rm lg}\hspace{0.1cm} (\frac{{\it \Phi}_{\rm V}(\tau_{\rm -30})}{{\it \Phi}_0}) = 10 \cdot {\rm lg}\hspace{0.1cm}\left [{\rm exp}[ -\frac{\tau_{\rm -30}}{ \tau_{\rm 0}}]\right ] \stackrel {!}{=} -30\,{\rm dB}$$
- $$\Rightarrow \hspace{0.3cm} {\rm lg}\hspace{0.1cm}\left [{\rm exp}[ -\frac{\tau_{\rm -30}}{ \tau_{\rm 0}}]\right ] = -3 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm ln}\hspace{0.1cm}\left [{\rm exp}[ -\frac{\tau_{\rm -30}}{ \tau_{\rm 0}}]\right ] = -3 \cdot {\rm ln}\hspace{0.1cm}(10)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \tau_{\rm 0} = \frac{\tau_{\rm -30}}{ 3 \cdot {\rm ln}\hspace{0.1cm}(10)}\approx \frac{\tau_{\rm -30}}{ 6.9} \hspace{0.05cm}.$$
Hierbei bezeichnet $\tau_{-30}$ die Verzögerungszeit, die zum logarithmischen Ordinatenwert $-30 \ \rm dB$ führt. Damit erhält man
- für ländliches Gebiet (Rural Area, RA) mit $\tau_{–30} = 0.75 \ \rm µ s$:
- $$\tau_{\rm 0} = \frac{0.75\,{\rm \mu s}}{ 6.9} \hspace{0.1cm}\underline {\approx 0.109\,{\rm µ s}} \hspace{0.05cm},$$
- für Städte und Vorote (Typical Urban, TU) mit $\tau_{–30} = 6.9 \ \rm µ s$:
- $$\tau_{\rm 0} = \frac{6.9\,{\rm \mu s}}{ 6.9} \hspace{0.1cm}\underline {\approx 1\,{\rm µ s}} \hspace{0.05cm},$$
(2) In der Aufgabe 2.7 wurde gezeigt, dass die Mehrwegeverbreitung $T_{\rm V} =\tau_0$ ist, wenn das Verzögerungs–Leistungsdichtespektrum entsprechend ${\rm e}^{-\tau/\tau_0}$ exponentiell abfällt. Es gilt demnach
- für „Rural Area”: $\hspace{0.4cm} T_{\rm V} \ \underline {= 0.109 \ \rm µ s}$,
- für „Typical Urban”: $\hspace{0.4cm} T_{\rm V} \ \underline {= 1 \ \rm µ s}$.
(3) In der Aufgabe A2.7 wurde auch gezeigt, dass für die Kohärenzbandbreite $B_{\rm K} \approx 0.276/\tau_0$ gilt. Daraus folgt:
- $B_{\rm K} \ \underline {\approx 2500 \ \rm kHz}$ („Rural Area”),
- $B_{\rm K} \ \underline {\approx 276 \ \rm kHz}$ („Typical Union”).
(4) Richtig ist hier der zweite Lösungsvorschlag:
- Frequenzselektivität des Mobilfunkkanals ist immer dann gegeben, wenn die Signalbandbreite $B_{\rm S}$ größer ist als die Kohärenzbandbreite $B_{\rm K}$ (oder zumindest in der gleichen Größenordnung liegt).
- Je kleiner $B_{\rm K}$ ist, um so häufiger ist dies der Fall.
(5) Entsprechend der angegebenen Gleichung ist ${\it \Phi}_{\rm V}(\tau = 5.001 \ \rm µ s)/{\it \Phi}_0 \hspace{0.15cm}\underline{\approx0.5}$.
- Dagegen gilt für geringfügig kleineres $\tau$ (zum Beispiel $\tau = 4.999 \ \rm µ s$) mit guter Näherung:
- $${{\it \Phi}_{\rm V}(\tau = 4.999\,{\rm \mu s})}/{{\it \Phi}_{\rm 0}} = {\rm e}^{ -{4.999\,{\rm µ s}}/{ 1\,{\rm \mu s}}} \approx {\rm e}^{-5} \hspace{0.1cm}\underline {= 0.00674 }\hspace{0.05cm}.$$
(6) Für die Leistung $P_1$ aller Signalanteile mit Verzögerungszeiten zwischen $0$ und $5 \ \rm s$ gilt:
- $$P_1 = {\it \Phi}_{\rm 0} \cdot \int_{0}^{5\,{\rm \mu s}} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} {\it \Phi}_{\rm 0} \cdot \int_{0}^{\infty} {\rm e}^{ -{\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau = {\it \Phi}_{\rm 0} \cdot \tau_0 \hspace{0.05cm}.$$
- Für den zweiten Anteil erhält man:
- $$P_2 = \frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{5\,{\rm µ s}}^{\infty} {\rm exp}[ \frac{5\,{\rm µ s} -\tau}{ \tau_0}] \hspace{0.15cm}{\rm d} \tau \hspace{0.15cm} \approx \hspace{0.15cm} \frac{{\it \Phi}_{\rm 0}}{2} \cdot \int_{0}^{\infty} {\rm exp}[ -{\tau}/{ \tau_0}] \hspace{0.15cm}{\rm d} \tau = \frac{{\it \Phi}_{\rm 0} \cdot \tau_0}{2} \hspace{0.05cm}. $$
- Entsprechend beträgt der prozentuale Anteil des ersten Anteils:
- $$\frac{P_1}{P_1+ P_2} = \frac{2}{3} \hspace{0.15cm}\underline {\approx 66.7\%}\hspace{0.05cm}.$$
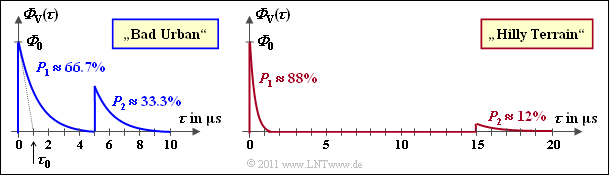
Die Grafik zeigt ${\it \Phi}_{\rm V}(\tau)$ in linearem Maßstab:
- Eingezeichnet sind die Flächen $P_1$ und $P_2$.
- Die linke Abbildung gilt für ${\rm BU}$, die rechte für ${\rm HT}$.
- Bei Letzterem beträgt der Leistungsanteil aller späteren Echos (später als $15 \ \rm µ s$) nur etwa $12\%$.
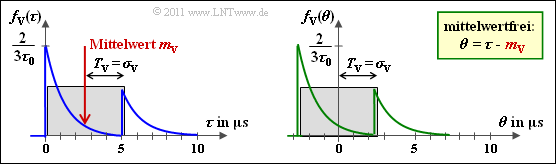
(7) Die Fläche über das gesamte Leistungsdichtespektrum ergibt $P = 1.5 \cdot \phi_0 \cdot \tau_0$.
- Normiert man ${\it \Phi}_{\rm V}(\tau)$ auf diesen Wert, so erhält man die Wahrscheinlichkeitsdichtefunktion $f_{\rm V}(\tau)$, wie in der nächsten Grafik dargestellt (linkes Diagramm).
- Mit $\tau_0 = 1 \ \rm µ s$, $\tau_5 = 5 \ \rm µ s$ ergibt sich für den linearen Mittelwert:
- $$m_{\rm V}= \int_{0}^{\infty} f_{\rm V}(\tau) \hspace{0.15cm}{\rm d} \tau$$
- $$\Rightarrow \hspace{0.3cm}m_{\rm V}= \frac{2}{3\tau_0} \cdot \int_{0}^{\tau_5} \tau \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau \ + $$
- $$ \hspace{1.7cm}+\ \frac{1}{3\tau_0} \cdot \int_{\tau_5}^{\infty} \tau \cdot {\rm e}^{ (\tau_5 -\tau)/\tau_0}\hspace{0.15cm}{\rm d} \tau \hspace{0.05cm}. $$
- Das erste Interal ist nach der angegebenen Gleichung gleich $2\tau_0/3$.
- Mit der Substitution $\tau' = \tau \, -\tau_5$ erhält man schließlich unter Verwendung der vorne angegebenen Integrallösungen:
- $$m_{\rm V} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{2\tau_0}{3} + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau') \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' = \frac{2\tau_0}{3} + \frac{\tau_5}{3\tau_0} \cdot \int_{0}^{\infty} \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} \tau' \cdot \cdot{\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' $$
- $$\Rightarrow \hspace{0.3cm}m_{\rm V}= \frac{2\tau_0}{3} + \frac{\tau_5}{3}+ \frac{\tau_0}{3} = \tau_0 + \frac{\tau_5}{3} \hspace{0.15cm}\underline {\approx 2.667\,{\rm µ s}} \hspace{0.05cm}. $$
- Die Varianz $\sigma_{\rm V}^2$ ist gleich dem quadratischen Mittelwert der mittelwertbefreiten Zufallsgröße $\theta = \tau \, –m_{\rm V}$, deren WDF in der rechten Grafik dargestellt ist.
- Daraus lässt sich $T_{\rm V} = \sigma_{\rm V}$ angeben.
- Eine zweite Möglichkeit besteht darin, zunächst den quadratischen Mittelwert der Zufallsgröße $\tau$ zu berechnen und daraus die Varianz $\sigma_{\rm V}^2$ mit dem Satz von Steiner.
- Mit den bereits oben beschriebenen Substitutionen und Näherungen erhält man so:
- $$m_{\rm V2} \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} \frac{2}{3\tau_0} \cdot \int_{0}^{\infty} \tau^2 \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau + \frac{1}{3\tau_0} \cdot \int_{0}^{\infty} (\tau_5 + \tau')^2 \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' $$
- $$\Rightarrow \hspace{0.3cm}m_{\rm V2} = \frac{2}{3} \cdot \int_{0}^{\infty} \frac{\tau^2}{\tau_0} \cdot {\rm e}^{ - {\tau}/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau + \frac{\tau_5^2}{3} \cdot \int_{0}^{\infty} \frac{1}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' +\frac{2\tau_5}{3} \cdot \int_{0}^{\infty} \frac{\tau '}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' + \frac{1}{3} \cdot \int_{0}^{\infty} \frac{{\tau '}^2}{\tau_0} \cdot {\rm e}^{ - {\tau}'/{ \tau_0}} \hspace{0.15cm}{\rm d} \tau ' \hspace{0.05cm}. $$
- Mit den vorne angegebenen Integralen folgt daraus:
- $$m_{\rm V2} \approx \frac{2}{3} \cdot 2 \tau_0^2 + \frac{\tau_5^2}{3} \cdot 1 + \frac{2\tau_5}{3} \cdot \tau_0 + \frac{1}{3} \cdot 2 \tau_0^2 = 2 \tau_0^2 + \frac{\tau_5^2}{3} + \frac{2 \cdot \tau_0 \cdot \tau_5}{3} $$
- $$\Rightarrow \hspace{0.3cm} \sigma_{\rm V}^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} m_{\rm V2} - m_{\rm V}^2 = 2 \tau_0^2 + \frac{\tau_5^2}{3} + \frac{2 \cdot \tau_0 \cdot \tau_5}{3} - (\tau_0 + \frac{\tau_5}{3})^2 =\tau_0^2 + \frac{2\tau_5^2}{9} = (1\,{\rm µ s})^2 + \frac{2\cdot (5\,{\rm µ s})^2}{9} = 6.55\,({\rm µ s})^2$$
- $$\Rightarrow \hspace{0.3cm} T_{\rm V} = \sigma_{\rm V} \hspace{0.15cm}\underline {\approx 2.56\,{\rm µ s}}\hspace{0.05cm}.$$
In obiger Grafik sind die Kenngrößen $T_{\rm V}$ und $\sigma_{\rm V}$ eingezeichnet.