Aufgaben:Aufgabe 2.7: Kohärenzbandbreite: Unterschied zwischen den Versionen
| Zeile 50: | Zeile 50: | ||
{Welche Gleichung gilt für die Frequenz–Korrelationsfunktion $\varphi_{\rm F}(\Delta f)$? | {Welche Gleichung gilt für die Frequenz–Korrelationsfunktion $\varphi_{\rm F}(\Delta f)$? | ||
| − | |type=" | + | |type="()"} |
+ $\varphi_{\rm F}(\Delta f) = \big[1/\tau_0 + {\rm j} \ 2 \pi \cdot \Delta f \big]^{-1}$, | + $\varphi_{\rm F}(\Delta f) = \big[1/\tau_0 + {\rm j} \ 2 \pi \cdot \Delta f \big]^{-1}$, | ||
- $\varphi_{\rm F}(\Delta f) = {\rm e}^ {-(\tau_0 \hspace{0.05cm}\cdot \hspace{0.05cm}\Delta f)^2}$. | - $\varphi_{\rm F}(\Delta f) = {\rm e}^ {-(\tau_0 \hspace{0.05cm}\cdot \hspace{0.05cm}\Delta f)^2}$. | ||
| Zeile 67: | Zeile 67: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | Damit erhält man für die Wahrscheinlichkeitsdichtefunktion: | + | *Damit erhält man für die Wahrscheinlichkeitsdichtefunktion: |
:$$f_{\rm V}(\tau) = \frac{{\it \Phi}_{\rm V}(\tau) }{{\it \Phi}_{\rm 0} \cdot \tau_0}= \frac{1}{\tau_0} \cdot {\rm e}^{-\tau / \tau_0} | :$$f_{\rm V}(\tau) = \frac{{\it \Phi}_{\rm V}(\tau) }{{\it \Phi}_{\rm 0} \cdot \tau_0}= \frac{1}{\tau_0} \cdot {\rm e}^{-\tau / \tau_0} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Richtig ist somit der <u>Lösungsvorschlag 2</u>. | + | *Richtig ist somit der <u>Lösungsvorschlag 2</u>. |
| − | '''(2)''' Das $k$–te Moment einer [[Stochastische_Signaltheorie/Exponentialverteilte_Zufallsgr%C3%B6%C3%9Fen#Einseitige_Exponentialverteilung| exponentialverteilten Zufallsgröße]] ist nach unserer Nomenklatur gleich $m_k = k! \cdot \tau_0^k$. Mit $k = 1$ ergibt sich daraus der lineare Mittelwert $m_1 = m_{\rm V}$: | + | |
| − | :$$m_{\rm V} = \tau_0 \hspace{0.1cm} \underline {= 1\,{\rm | + | '''(2)''' Das $k$–te Moment einer [[Stochastische_Signaltheorie/Exponentialverteilte_Zufallsgr%C3%B6%C3%9Fen#Einseitige_Exponentialverteilung| exponentialverteilten Zufallsgröße]] ist nach unserer Nomenklatur gleich $m_k = k! \cdot \tau_0^k$. |
| + | *Mit $k = 1$ ergibt sich daraus der lineare Mittelwert $m_1 = m_{\rm V}$: | ||
| + | :$$m_{\rm V} = \tau_0 \hspace{0.1cm} \underline {= 1\,{\rm µ s}} | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | '''(3)''' Nach dem [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Einige_h.C3.A4ufig_benutzte_Zentralmomente| Satz von Steiner]] gilt für die Varianz einer Zufallsgröße allgemein: $\sigma^2 = m_2 \, –m_1^2$. Nach der oben angegebenen Gleichung ist $m_2 = 2 \cdot \tau_0^2$. Daraus folgt: | + | |
| + | '''(3)''' Nach dem [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Einige_h.C3.A4ufig_benutzte_Zentralmomente| Satz von Steiner]] gilt für die Varianz einer Zufallsgröße allgemein: $\sigma^2 = m_2 \, –m_1^2$. | ||
| + | *Nach der oben angegebenen Gleichung ist $m_2 = 2 \cdot \tau_0^2$. Daraus folgt: | ||
:$$\sigma_{\rm V}^2 = m_2 - m_1^2 = 2 \cdot \tau_0^2 - (\tau_0)^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | :$$\sigma_{\rm V}^2 = m_2 - m_1^2 = 2 \cdot \tau_0^2 - (\tau_0)^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| − | \sigma_{\rm V} = \tau_0 \hspace{0.1cm} \underline {= 1\,{\rm | + | \sigma_{\rm V} = \tau_0 \hspace{0.1cm} \underline {= 1\,{\rm µ s}} |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | '''(4)''' ${\it \Phi}_{\rm V}(\tau)$ ist identisch mit dem in der Hilfsgleichung angegebenen $x(t)$, wenn man $t$ durch $\tau$ und $\lambda$ durch $1/\tau_0$ ersetzt. Damit hat $\varphi_{\rm F}(\Delta f)$ den gleichen Verlauf wie $X(f)$ mit der Substitution $f → \Delta f$: | + | |
| + | '''(4)''' ${\it \Phi}_{\rm V}(\tau)$ ist identisch mit dem in der Hilfsgleichung angegebenen $x(t)$, wenn man $t$ durch $\tau$ und $\lambda$ durch $1/\tau_0$ ersetzt. | ||
| + | *Damit hat $\varphi_{\rm F}(\Delta f)$ den gleichen Verlauf wie $X(f)$ mit der Substitution $f → \Delta f$: | ||
:$$\varphi_{\rm F}(\Delta f) = \frac{1}{1/\tau_0 + {\rm j} \cdot 2\pi \Delta f} | :$$\varphi_{\rm F}(\Delta f) = \frac{1}{1/\tau_0 + {\rm j} \cdot 2\pi \Delta f} | ||
= \frac{\tau_0}{1 + {\rm j} \cdot 2\pi \cdot \tau_0 \cdot \Delta f}\hspace{0.05cm}.$$ | = \frac{\tau_0}{1 + {\rm j} \cdot 2\pi \cdot \tau_0 \cdot \Delta f}\hspace{0.05cm}.$$ | ||
| − | Richtig ist die <u>erste Gleichung</u>. | + | *Richtig ist die <u>erste Gleichung</u>. |
| + | |||
| Zeile 99: | Zeile 106: | ||
B_{\rm K}= \frac{\sqrt{3}}{2\pi \cdot \tau_0} \approx \frac{0.276}{ \tau_0}\hspace{0.05cm}. $$ | B_{\rm K}= \frac{\sqrt{3}}{2\pi \cdot \tau_0} \approx \frac{0.276}{ \tau_0}\hspace{0.05cm}. $$ | ||
| − | Mit $\tau_0 = 1 \ \rm | + | *Mit $\tau_0 = 1 \ \rm µ s$ folgt daraus für die Kohärenzbandbreite $B_{\rm K} \ \underline {= 276 \ \rm kHz}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Aufgaben zu Mobile Kommunikation|^2.3 Das GWSSUS–Kanalmodell^]] | [[Category:Aufgaben zu Mobile Kommunikation|^2.3 Das GWSSUS–Kanalmodell^]] | ||
Version vom 13. April 2019, 15:24 Uhr
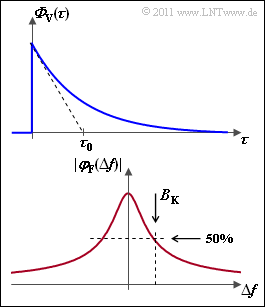
Für das Verzögerungs–Leistungsdichtespektrum wählen wir einen exponentiellen Ansatz. Mit ${\it \Phi}_0 = {\it \Phi}_{\rm V}(\tau = 0)$ gilt:
- $${{\it \Phi}_{\rm V}(\tau)}/{{\it \Phi}_{\rm 0}} = {\rm e}^{ -\tau / \tau_0 } \hspace{0.05cm}.$$
Die Konstante $\tau_0$ lässt sich entsprechend der oberen Grafik aus der Tangente im Punkt $\tau = 0$ ermitteln. Beachten Sie, dass ${\it \Phi}_{\rm V}(\tau)$ die Einheit $[1/\rm s]$ aufweist. Weiter gilt:
- Die Wahrscheinlichkeitsdichte $f_{\rm V}(\tau)$ hat gleiche Form wie ${\it \Phi}_{\rm V}(\tau)$, ist jedoch auf die Fläche $1$ normiert.
- Die mittlere Verzögerungszeit (englisch: Average Excess Delay) $m_{\rm V}$ ist gleich dem linearen Erwartungswert $E\big [\tau \big]$ und lässt sich aus der WDF $f_{\rm V}(\tau)$ bestimmen.
- Die Mehrwegeverbreiterung (englisch: Multipath Spread) $\sigma_{\rm V}$ gibt die Standardabweichung (Streuung) der Zufallsgröße $\tau$ an. Im Theorieteil verwenden wir hierfür auch die Bezeichnung $T_{\rm V}$.
- Die dargestellte Frequenz–Korrelationsfunktion $\varphi_{\rm F}(\Delta f)$ kann als die Fouriertransformierte des Verzögerungs–Leistungsdichtespektrum ${\it \Phi}_{\rm V}(\tau)$ berechnet werden:
- $$\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}.$$
- Die Kohärenzbandbreite $B_{\rm K}$ ist der $\Delta f$–Wert, bei dem die Frequenz–Korrelationsfunktion $\varphi_{\rm F}(\Delta f)$ auf den halben Betrag abgefallen ist.
Hinweise:
- Die Aufgabe gehört zum Themengebiet des Kapitels GWSSUS–Kanalmodell.
- Benötigt werden Kenntnisse zur Momentenberechnung von Zufallsgrößen aus dem Buch „Stochastische Signaltheorie”.
- Außerdem kann folgende Fouriertransformation als gegeben vorausgesetzt werden:
- $$x(t) = \left\{ \begin{array}{c} {\rm e}^{- \lambda \hspace{0.05cm}\cdot \hspace{0.05cm} t}\\ 0 \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.35cm} {\rm f\ddot{u}r} \hspace{0.15cm} t \ge 0 \\ \hspace{-0.35cm} {\rm f\ddot{u}r} \hspace{0.15cm} t < 0 \\ \end{array} \hspace{0.4cm} {\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.4cm} X(f) = \frac{1}{\lambda + {\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$\int_{0}^{+\infty} {\it \Phi}_{\rm V}(\tau) \hspace{0.15cm}{\rm d} \tau = {\it \Phi}_{\rm 0} \cdot \int_{0}^{+\infty} {\rm e}^{-\tau / \tau_0} \hspace{0.15cm}{\rm d} \tau = {\it \Phi}_{\rm 0} \cdot \tau_0 \hspace{0.05cm}. $$
- Damit erhält man für die Wahrscheinlichkeitsdichtefunktion:
- $$f_{\rm V}(\tau) = \frac{{\it \Phi}_{\rm V}(\tau) }{{\it \Phi}_{\rm 0} \cdot \tau_0}= \frac{1}{\tau_0} \cdot {\rm e}^{-\tau / \tau_0} \hspace{0.05cm}.$$
- Richtig ist somit der Lösungsvorschlag 2.
(2) Das $k$–te Moment einer exponentialverteilten Zufallsgröße ist nach unserer Nomenklatur gleich $m_k = k! \cdot \tau_0^k$.
- Mit $k = 1$ ergibt sich daraus der lineare Mittelwert $m_1 = m_{\rm V}$:
- $$m_{\rm V} = \tau_0 \hspace{0.1cm} \underline {= 1\,{\rm µ s}} \hspace{0.05cm}. $$
(3) Nach dem Satz von Steiner gilt für die Varianz einer Zufallsgröße allgemein: $\sigma^2 = m_2 \, –m_1^2$.
- Nach der oben angegebenen Gleichung ist $m_2 = 2 \cdot \tau_0^2$. Daraus folgt:
- $$\sigma_{\rm V}^2 = m_2 - m_1^2 = 2 \cdot \tau_0^2 - (\tau_0)^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma_{\rm V} = \tau_0 \hspace{0.1cm} \underline {= 1\,{\rm µ s}} \hspace{0.05cm}. $$
(4) ${\it \Phi}_{\rm V}(\tau)$ ist identisch mit dem in der Hilfsgleichung angegebenen $x(t)$, wenn man $t$ durch $\tau$ und $\lambda$ durch $1/\tau_0$ ersetzt.
- Damit hat $\varphi_{\rm F}(\Delta f)$ den gleichen Verlauf wie $X(f)$ mit der Substitution $f → \Delta f$:
- $$\varphi_{\rm F}(\Delta f) = \frac{1}{1/\tau_0 + {\rm j} \cdot 2\pi \Delta f} = \frac{\tau_0}{1 + {\rm j} \cdot 2\pi \cdot \tau_0 \cdot \Delta f}\hspace{0.05cm}.$$
- Richtig ist die erste Gleichung.
(5) Die Kohärenzbandbreite ergibt sich implizit aus der folgenden Gleichung:
- $$|\varphi_{\rm F}(\Delta f = B_{\rm K})| \stackrel {!}{=} \frac{1}{2} \cdot |\varphi_{\rm F}(\Delta f = 0)| = \frac{\tau_0}{2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}|\varphi_{\rm F}(\Delta f = B_{\rm K})|^2 = \frac{\tau_0^2}{1 + (2\pi \cdot \tau_0 \cdot B_{\rm K})^2} \stackrel {!}{=} \frac{\tau_0^2}{4}$$
- $$\Rightarrow \hspace{0.3cm}(2\pi \cdot \tau_0 \cdot B_{\rm K})^2 = 3 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} B_{\rm K}= \frac{\sqrt{3}}{2\pi \cdot \tau_0} \approx \frac{0.276}{ \tau_0}\hspace{0.05cm}. $$
- Mit $\tau_0 = 1 \ \rm µ s$ folgt daraus für die Kohärenzbandbreite $B_{\rm K} \ \underline {= 276 \ \rm kHz}$.