Digitalsignalübertragung/Symbolweise Codierung mit Pseudoternärcodes: Unterschied zwischen den Versionen
| Zeile 9: | Zeile 9: | ||
== Allgemeine Beschreibung der Pseudomehrstufencodes == | == Allgemeine Beschreibung der Pseudomehrstufencodes == | ||
<br> | <br> | ||
| − | Bei der symbolweisen Codierung wird mit jedem ankommenden Quellensymbol $q_\nu$ ein Codesymbol $c_\nu$ erzeugt, das außer vom aktuellen Eingangssymbol $q_\nu$ auch von den $N_{\rm C}$ vorangegangenen Symbolen $q_\nu$, ... , $q_{\nu-N_{\rm C}} $ abhängt. $N_{\rm C}$ bezeichnet man als die ''Ordnung'' des Codes.<br><br> | + | Bei der symbolweisen Codierung wird mit jedem ankommenden Quellensymbol $q_\nu$ ein Codesymbol $c_\nu$ erzeugt, das außer vom aktuellen Eingangssymbol $q_\nu$ auch von den $N_{\rm C}$ vorangegangenen Symbolen $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}} $ abhängt. $N_{\rm C}$ bezeichnet man als die ''Ordnung'' des Codes.<br><br> |
Typisch für eine symbolweise Codierung ist, dass | Typisch für eine symbolweise Codierung ist, dass | ||
| − | *die Symboldauer $T$ des Codersignals (und des Sendesignals) mit der Bitdauer $T_{\rm B}$ des binären Quellensignals übereinstimmt, und | + | *die Symboldauer $T$ des Codersignals (und des Sendesignals) mit der Bitdauer $T_{\rm B}$ des binären Quellensignals übereinstimmt, und |
| − | * | + | *Codierung und Decodierung nicht zu größeren Zeitverzögerungen führen, die bei Verwendung von Blockcodes unvermeidbar sind.<br><br> |
| − | Besondere Bedeutung besitzen die ''Pseudomehrstufencodes'' – besser bekannt unter der englischen Bezeichnung ''Partial Response Codes''.<br> | + | Besondere Bedeutung besitzen die ''Pseudomehrstufencodes'' – besser bekannt unter der englischen Bezeichnung ''Partial Response Codes''.<br> |
| − | Im Folgenden werden ausschließlich ''Pseudoternärcodes'' ⇒ Stufenzahl $M = 3$ betrachtet, die durch das Blockschaltbild entsprechend der linken Grafik beschreibbar sind. In der rechten Grafik ist ein Ersatzschaltbild angegeben, das für eine Analyse dieser Codes sehr gut geeignet ist. | + | Im Folgenden werden ausschließlich ''Pseudoternärcodes'' ⇒ Stufenzahl $M = 3$ betrachtet, die durch das Blockschaltbild entsprechend der linken Grafik beschreibbar sind. In der rechten Grafik ist ein Ersatzschaltbild angegeben, das für eine Analyse dieser Codes sehr gut geeignet ist. |
| − | [[Datei:P_ID1343__Dig_T_2_4_S1_v1.png|center|frame|Blockschaltbild und Ersatzschaltbild eines | + | [[Datei:P_ID1343__Dig_T_2_4_S1_v1.png|center|frame|Blockschaltbild und Ersatzschaltbild eines Pseudoternärcoders|class=fit]] |
Man erkennt aus den beiden Darstellungen: | Man erkennt aus den beiden Darstellungen: | ||
| − | *Der Pseudoternärcoder kann in den nichtlinearen Vorcodierer und ein lineares Codiernetzwerk aufgespalten werden, wenn man – wie im rechten Ersatzschaltbild dargestellt – die Verzögerung um $N_{\rm C} \cdot T$ und die Gewichtung mit $K_{\rm C}$ zur Verdeutlichung zweimal zeichnet.<br> | + | *Der Pseudoternärcoder kann in den nichtlinearen Vorcodierer und ein lineares Codiernetzwerk aufgespalten werden, wenn man – wie im rechten Ersatzschaltbild dargestellt – die Verzögerung um $N_{\rm C} \cdot T$ und die Gewichtung mit $K_{\rm C}$ zur Verdeutlichung zweimal zeichnet.<br> |
| − | *Der ''nichtlineare Vorcodierer'' gewinnt durch eine Modulo–2–Addition (''Antivalenz'') zwischen den Symbolen $q_\nu$ und $K_{\rm C} \cdot b_{\nu-N_{\rm C}} $ die vorcodierten Symbole $b_\nu$, die ebenfalls binär sind: | + | *Der ''nichtlineare Vorcodierer'' gewinnt durch eine Modulo–2–Addition (''Antivalenz'' ) zwischen den Symbolen $q_\nu$ und $K_{\rm C} \cdot b_{\nu-N_{\rm C}} $ die vorcodierten Symbole $b_\nu$, die ebenfalls binär sind: |
:$$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, | :$$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, | ||
+1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, | +1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, | ||
+1\}\hspace{0.05cm}.$$ | +1\}\hspace{0.05cm}.$$ | ||
| − | *Die Symbole $b_\nu$ sind wie die Quellensymbole $q_\nu$ statistisch voneinander unabhängig. Der Vorcodierer fügt also keine Redundanz hinzu. Er gestattet aber eine einfachere Realisierung des Decoders und verhindert eine Fehlerfortpflanzung nach einem Übertragungsfehler.<br> | + | *Die Symbole $b_\nu$ sind wie die Quellensymbole $q_\nu$ statistisch voneinander unabhängig. Der Vorcodierer fügt also keine Redundanz hinzu. Er gestattet aber eine einfachere Realisierung des Decoders und verhindert eine Fehlerfortpflanzung nach einem Übertragungsfehler.<br> |
| − | *Die eigentliche Umcodierung von binär $(M_q = 2)$ auf ternär $(M = M_c = 3)$ bewirkt das ''lineare Codiernetzwerk'' durch die herkömmliche Subtraktion | + | *Die eigentliche Umcodierung von binär $(M_q = 2)$ auf ternär $(M = M_c = 3)$ bewirkt das ''lineare Codiernetzwerk'' durch die herkömmliche Subtraktion |
:$$c(t) ={1}/{2} \cdot \big [b(t) - K_{\rm C} \cdot b(t- N_{\rm | :$$c(t) ={1}/{2} \cdot \big [b(t) - K_{\rm C} \cdot b(t- N_{\rm | ||
C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$ | C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$ | ||
| − | :das durch folgende [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Impulsantwort|Impulsantwort]] bzw. [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|Übertragungsfunktion]] bezüglich dem Eingangssignal $b(t)$ und dem Eingangssignal $c(t)$beschrieben werden kann: | + | :das durch folgende [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Impulsantwort|Impulsantwort]] bzw. [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|Übertragungsfunktion]] bezüglich dem Eingangssignal $b(t)$ und dem Eingangssignal $c(t)$ beschrieben werden kann: |
:$$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm | :$$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm | ||
C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$ | C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$ | ||
| − | *Die relative Coderedundanz ist für alle Pseudoternärcodes gleich. Setzt man in die [[Digitalsignalübertragung/Redundanzfreie_Codierung#Blockweise_Codierung_vs._symbolweise_Codierung| | + | *Die relative Coderedundanz ist für alle Pseudoternärcodes gleich. Setzt man in die [[Digitalsignalübertragung/Redundanzfreie_Codierung#Blockweise_Codierung_vs._symbolweise_Codierung|allgemeine Definitionsgleichung]] $M_q=2$, $M_c=3$ und $T_c =T_q$ ein, so erhält man |
:$$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.5cm}\Rightarrow \hspace{0.5cm} r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$ | :$$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.5cm}\Rightarrow \hspace{0.5cm} r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Fazit:}$ | + | $\text{Fazit:}$ Wird für den Sendegrundimpuls $g_s(t)$ das NRZ–Rechteck vorausgesetzt, so lautet das '''Sendesignal aller Pseudoternärcodes''': |
:$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.05cm}.$$ | :$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.05cm}.$$ | ||
Dieses ist sowohl ''ternär'' ⇒ $a_\nu \in \{-1, \ 0, +1\}$ als auch ''redundant'' ⇒ statistische Bindungen zwischen den $a_\nu$.}} | Dieses ist sowohl ''ternär'' ⇒ $a_\nu \in \{-1, \ 0, +1\}$ als auch ''redundant'' ⇒ statistische Bindungen zwischen den $a_\nu$.}} | ||
| Zeile 48: | Zeile 48: | ||
== Eigenschaften des AMI-Codes== | == Eigenschaften des AMI-Codes== | ||
<br> | <br> | ||
| − | Die einzelnen Pseudoternärcodes unterscheiden sich in den Parametern $N_{\rm C}$ und $K_{\rm C}$. | + | Die einzelnen Pseudoternärcodes unterscheiden sich in den Parametern $N_{\rm C}$ und $K_{\rm C}$. |
| − | Der bekannteste Vertreter ist der '''Bipolarcode erster Ordnung''' mit den Codeparametern $N_{\rm C} = 1$ und $K_{\rm C} = 1$, der auch unter der Bezeichnung '''AMI–Code''' (von: ''Alternate Mark Inversion'') bekannt ist. Dieser wird zum Beispiel bei [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_ISDN|ISDN]] (''Integrated Services Digital Networks'') auf der so genannten $S_0$–Schnittstelle eingesetzt. | + | Der bekannteste Vertreter ist der '''Bipolarcode erster Ordnung''' mit den Codeparametern $N_{\rm C} = 1$ und $K_{\rm C} = 1$, der auch unter der Bezeichnung '''AMI–Code''' (von: ''Alternate Mark Inversion'') bekannt ist. Dieser wird zum Beispiel bei [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_ISDN|ISDN]] (''Integrated Services Digital Networks'') auf der so genannten $S_0$–Schnittstelle eingesetzt. |
[[Datei:P_ID1346__Dig_T_2_4_S2a_v1.png|right|frame|Signale bei AMI- und HDB3-Codierung|class=fit]] | [[Datei:P_ID1346__Dig_T_2_4_S2a_v1.png|right|frame|Signale bei AMI- und HDB3-Codierung|class=fit]] | ||
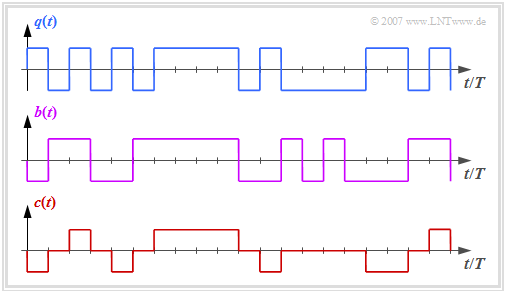
| − | Die Grafik zeigt oben das binäre Quellensignal $q(t)$. Im zweiten und dritten Diagramm sind dargestellt: | + | Die Grafik zeigt oben das binäre Quellensignal $q(t)$. Im zweiten und dritten Diagramm sind dargestellt: |
| − | * das ebenfalls binäre Signal $b(t)$ nach dem Vorcodierer, und | + | * das ebenfalls binäre Signal $b(t)$ nach dem Vorcodierer, und |
| − | * das Codersignal $c(t) = s(t)$ | + | * das Codersignal $c(t) = s(t)$ des AMI–Codes. |
| − | Man erkennt das einfache AMI– | + | Man erkennt das einfache AMI–Codierprinzip: |
| − | *Jeder Binärwert „–1” von $q(t)$ ⇒ Symbol $\rm L$ wird durch den ternären Amplitudenkoeffizienten $a_\nu = 0$ codiert.<br> | + | *Jeder Binärwert „–1” von $q(t)$ ⇒ Symbol $\rm L$ wird durch den ternären Amplitudenkoeffizienten $a_\nu = 0$ codiert.<br> |
| − | *Der Binärwert „+1” von $q(t)$ ⇒ Symbol $\rm H$ wird alternierend mit $a_\nu = +1$ und $a_\nu = -1$ dargestellt.<br><br> | + | *Der Binärwert „+1” von $q(t)$ ⇒ Symbol $\rm H$ wird alternierend mit $a_\nu = +1$ und $a_\nu = -1$ dargestellt.<br><br> |
Damit wird sichergestellt, dass im AMI–codierten Signal keine langen „+1”– bzw. „–1”–Sequenzen enthalten sind, was bei einem gleichsignalfreien Kanal zu Problemen führen würde. | Damit wird sichergestellt, dass im AMI–codierten Signal keine langen „+1”– bzw. „–1”–Sequenzen enthalten sind, was bei einem gleichsignalfreien Kanal zu Problemen führen würde. | ||
| Zeile 66: | Zeile 66: | ||
Dagegen ist das Auftreten langer Nullfolgen durchaus möglich, bei denen über einen längeren Zeitraum keine Taktinformation übertragen wird. | Dagegen ist das Auftreten langer Nullfolgen durchaus möglich, bei denen über einen längeren Zeitraum keine Taktinformation übertragen wird. | ||
<br clear = all> | <br clear = all> | ||
| − | Um dieses zweite Problem zu vermeiden, wurden einige modifizierte AMI–Codes entwickelt, zum Beispiel der ''B6ZS–Code'' und der ''HDB3''–Code: | + | Um dieses zweite Problem zu vermeiden, wurden einige modifizierte AMI–Codes entwickelt, zum Beispiel der ''B6ZS–Code'' und der ''HDB3''–Code: |
| − | *Beim '''HDB3–Code''' (grüne Kurve in obiger Grafik) werden vier aufeinanderfolgende Nullen im AMI–codierten Signal durch eine Teilsequenz ersetzt, die die AMI–Codierregel verletzt.<br> | + | *Beim '''HDB3–Code''' (grüne Kurve in obiger Grafik) werden vier aufeinanderfolgende Nullen im AMI–codierten Signal durch eine Teilsequenz ersetzt, die die AMI–Codierregel verletzt.<br> |
*Im grau hinterlegten Bereich ist dies die Folge „+ 0 0 +”, da das letzte Symbol vor der Ersetzung ein „Minus” war.<br> | *Im grau hinterlegten Bereich ist dies die Folge „+ 0 0 +”, da das letzte Symbol vor der Ersetzung ein „Minus” war.<br> | ||
| − | *Damit ist beim HDB3–Code die Anzahl aufeinanderfolgender Nullen auf $3$ begrenzt | + | *Damit ist beim HDB3–Code die Anzahl aufeinanderfolgender Nullen auf $3$ begrenzt und beim [https://www.itwissen.info/B6ZS-bipolar-with-six-zero-substitution-B6ZS-Codierung.html B6ZS–Code] auf $5$. |
*Der Decoder erkennt diese Codeverletzung und ersetzt „+ 0 0 +” wieder durch „0 0 0 0”.<br> | *Der Decoder erkennt diese Codeverletzung und ersetzt „+ 0 0 +” wieder durch „0 0 0 0”.<br> | ||
| Zeile 86: | Zeile 86: | ||
\big ]\hspace{0.05cm}.$$ | \big ]\hspace{0.05cm}.$$ | ||
| − | Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten ( | + | Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten $(K$ und $\alpha$ sind Abkürzungen entsprechend obiger Gleichung$)$: |
:$$ {\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = \frac{\big [1 - K \cos | :$$ {\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = \frac{\big [1 - K \cos | ||
(\alpha) + {\rm j}\cdot K \sin (\alpha) \big ] \big [1 - K \cos | (\alpha) + {\rm j}\cdot K \sin (\alpha) \big ] \big [1 - K \cos | ||
| Zeile 96: | Zeile 96: | ||
\hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} | \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} | ||
\varphi_a(\lambda \cdot T)\hspace{0.05cm}.$$ | \varphi_a(\lambda \cdot T)\hspace{0.05cm}.$$ | ||
| − | |||
Insbesondere erhält man für das Leistungsdichtespektrum (LDS) des AMI–Codes $(N_{\rm C} = K_{\rm C} = 1)$: | Insbesondere erhält man für das Leistungsdichtespektrum (LDS) des AMI–Codes $(N_{\rm C} = K_{\rm C} = 1)$: | ||
| Zeile 104: | Zeile 103: | ||
Die Grafik zeigt | Die Grafik zeigt | ||
| − | *das LDS ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten (rote Kurve),<br> | + | *das LDS ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten (rote Kurve), und<br> |
| − | *das LDS ${\it \Phi}_s(f)$ des gesamten Sendesignals (blau), gültig für NRZ–Rechteckimpulse.<br> | + | *das LDS ${\it \Phi}_s(f)$ des gesamten Sendesignals (blau), gültig für NRZ–Rechteckimpulse.<br> |
Man erkennt aus dieser Darstellung | Man erkennt aus dieser Darstellung | ||
| − | *die Gleichsignalfreiheit des AMI–Codes, da ${\it \Phi}_a(f = 0) = {\it \Phi}_s(f = 0) = 0$ ist,<br> | + | *die Gleichsignalfreiheit des AMI–Codes, da ${\it \Phi}_a(f = 0) = {\it \Phi}_s(f = 0) = 0$ ist,<br> |
| − | *die Leistung $P_{\rm S} = s_0^2/$ des AMI–codierten Sendesignals (Integral über ${\it \Phi}_s(f)$ von $- \infty$ bis $+\infty$). | + | *die Leistung $P_{\rm S} = s_0^2/2$ des AMI–codierten Sendesignals (Integral über ${\it \Phi}_s(f)$ von $- \infty$ bis $+\infty$). |
''Hinweise:'' | ''Hinweise:'' | ||
*Das LDS von HDB3– und B6ZS–Code weicht von dem des AMI–Codes nur unwesentlich ab.<br> | *Das LDS von HDB3– und B6ZS–Code weicht von dem des AMI–Codes nur unwesentlich ab.<br> | ||
| − | *Die hier behandelte Thematik können Sie sich mit dem | + | *Die hier behandelte Thematik können Sie sich mit dem interaktiven Applet [[Applets:Pseudoternaercodierung|Signale, AKF und LDS der Pseudoternärcodes]] verdeutlichen. |
== Eigenschaften des Duobinärcodes == | == Eigenschaften des Duobinärcodes == | ||
<br> | <br> | ||
| − | |||
[[Datei:P_ID1348__Dig_T_2_4_S3b_v1.png|right|frame|Leistungsdichtespektrum des Duobinärcodes|right|class=fit]] | [[Datei:P_ID1348__Dig_T_2_4_S3b_v1.png|right|frame|Leistungsdichtespektrum des Duobinärcodes|right|class=fit]] | ||
| + | Der '''Duobinärcode''' ist durch die Codeparameter $N_{\rm C} = 1$ und $K_{\rm C} = -1$ festgelegt. Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten bzw. für das LDS des Sendesignals: | ||
| + | |||
:$${\it \Phi}_a(f) ={1}/{2} \cdot \big [1 + \cos | :$${\it \Phi}_a(f) ={1}/{2} \cdot \big [1 + \cos | ||
(2\pi f T)\big ] = \cos^2 | (2\pi f T)\big ] = \cos^2 | ||
| Zeile 131: | Zeile 131: | ||
Die Grafik zeigt das Leistungsdichtespektrum | Die Grafik zeigt das Leistungsdichtespektrum | ||
| − | *der Amplitudenkoeffizienten ⇒ ${\it \Phi}_a(f)$ als rote Kurve,<br> | + | *der Amplitudenkoeffizienten ⇒ ${\it \Phi}_a(f)$ als rote Kurve,<br> |
| − | *des gesamten Sendsignals ⇒ ${\it \Phi}_s(f)$ als blaue Kurve.<br><br> | + | *des gesamten Sendsignals ⇒ ${\it \Phi}_s(f)$ als blaue Kurve.<br><br> |
| − | In der zweiten Grafik sind die Signale $q(t)$, $b(t)$ und $c(t) = s(t)$ skizziert. Wir verweisen hier wieder auf das | + | In der zweiten Grafik sind die Signale $q(t)$, $b(t)$ und $c(t) = s(t)$ skizziert. Wir verweisen hier wieder auf das Applet [[Applets:Pseudoternaercodierung|Signale, AKF und LDS der Pseudoternärcodes]], das auch die Eigenschaften des Duobinärcodes verdeutlicht. |
[[Datei:P_ID1349__Dig_T_2_4_S3a_v2.png|left|frame|Signale bei Duobinärcodierung|class=fit]] | [[Datei:P_ID1349__Dig_T_2_4_S3a_v2.png|left|frame|Signale bei Duobinärcodierung|class=fit]] | ||
| − | + | <br><br>Aus diesen Darstellungen geht hervor: | |
*Beim Duobinärcode können beliebig viele Symbole mit gleicher Polarität („+1” bzw. „–1”) direkt aufeinanderfolgen. | *Beim Duobinärcode können beliebig viele Symbole mit gleicher Polarität („+1” bzw. „–1”) direkt aufeinanderfolgen. | ||
| − | *Deshalb gilt ${\it \Phi}_a(f = 0)$ und ${\it \Phi}_s(f = 0) = 1/2 \cdot s_0^2 \cdot T$.<br> | + | *Deshalb gilt ${\it \Phi}_a(f = 0)=1$ und ${\it \Phi}_s(f = 0) = 1/2 \cdot s_0^2 \cdot T$.<br> |
| − | *Dagegen tritt beim Duobinärcode die alternierende Folge „ ... , +1, –1, +1, –1, +1, ... ” nicht auf, die hinsichtlich Impulsinterferenzen besonders störend ist. Deshalb gilt | + | *Dagegen tritt beim Duobinärcode die alternierende Folge „ ... , +1, –1, +1, –1, +1, ... ” nicht auf, die hinsichtlich Impulsinterferenzen besonders störend ist. |
| − | * | + | *Deshalb gilt beim Duobinärcode: ${\it \Phi}_s(f = 1/(2T) = 0$.<br> |
| + | *Das Leistungsdichtespektrum ${\it \Phi}_s(f)$ des pseudoternären Duobinärcodes ist identisch mit dem LDS bei redundanzfreier Binärcodierung mit halber Rate $($Symboldauer $2T)$.<br> | ||
<br clear= all> | <br clear= all> | ||
Version vom 14. Februar 2019, 11:54 Uhr
Inhaltsverzeichnis
Allgemeine Beschreibung der Pseudomehrstufencodes
Bei der symbolweisen Codierung wird mit jedem ankommenden Quellensymbol $q_\nu$ ein Codesymbol $c_\nu$ erzeugt, das außer vom aktuellen Eingangssymbol $q_\nu$ auch von den $N_{\rm C}$ vorangegangenen Symbolen $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}} $ abhängt. $N_{\rm C}$ bezeichnet man als die Ordnung des Codes.
Typisch für eine symbolweise Codierung ist, dass
- die Symboldauer $T$ des Codersignals (und des Sendesignals) mit der Bitdauer $T_{\rm B}$ des binären Quellensignals übereinstimmt, und
- Codierung und Decodierung nicht zu größeren Zeitverzögerungen führen, die bei Verwendung von Blockcodes unvermeidbar sind.
Besondere Bedeutung besitzen die Pseudomehrstufencodes – besser bekannt unter der englischen Bezeichnung Partial Response Codes.
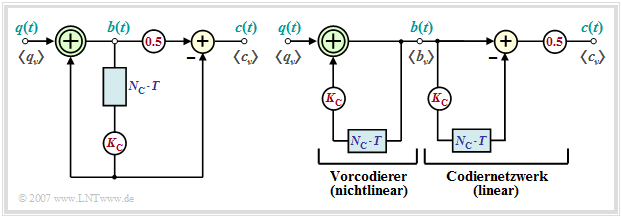
Im Folgenden werden ausschließlich Pseudoternärcodes ⇒ Stufenzahl $M = 3$ betrachtet, die durch das Blockschaltbild entsprechend der linken Grafik beschreibbar sind. In der rechten Grafik ist ein Ersatzschaltbild angegeben, das für eine Analyse dieser Codes sehr gut geeignet ist.
Man erkennt aus den beiden Darstellungen:
- Der Pseudoternärcoder kann in den nichtlinearen Vorcodierer und ein lineares Codiernetzwerk aufgespalten werden, wenn man – wie im rechten Ersatzschaltbild dargestellt – die Verzögerung um $N_{\rm C} \cdot T$ und die Gewichtung mit $K_{\rm C}$ zur Verdeutlichung zweimal zeichnet.
- Der nichtlineare Vorcodierer gewinnt durch eine Modulo–2–Addition (Antivalenz ) zwischen den Symbolen $q_\nu$ und $K_{\rm C} \cdot b_{\nu-N_{\rm C}} $ die vorcodierten Symbole $b_\nu$, die ebenfalls binär sind:
- $$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, +1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, +1\}\hspace{0.05cm}.$$
- Die Symbole $b_\nu$ sind wie die Quellensymbole $q_\nu$ statistisch voneinander unabhängig. Der Vorcodierer fügt also keine Redundanz hinzu. Er gestattet aber eine einfachere Realisierung des Decoders und verhindert eine Fehlerfortpflanzung nach einem Übertragungsfehler.
- Die eigentliche Umcodierung von binär $(M_q = 2)$ auf ternär $(M = M_c = 3)$ bewirkt das lineare Codiernetzwerk durch die herkömmliche Subtraktion
- $$c(t) ={1}/{2} \cdot \big [b(t) - K_{\rm C} \cdot b(t- N_{\rm C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$
- das durch folgende Impulsantwort bzw. Übertragungsfunktion bezüglich dem Eingangssignal $b(t)$ und dem Eingangssignal $c(t)$ beschrieben werden kann:
- $$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$
- Die relative Coderedundanz ist für alle Pseudoternärcodes gleich. Setzt man in die allgemeine Definitionsgleichung $M_q=2$, $M_c=3$ und $T_c =T_q$ ein, so erhält man
- $$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.5cm}\Rightarrow \hspace{0.5cm} r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$
$\text{Fazit:}$ Wird für den Sendegrundimpuls $g_s(t)$ das NRZ–Rechteck vorausgesetzt, so lautet das Sendesignal aller Pseudoternärcodes:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.05cm}.$$
Dieses ist sowohl ternär ⇒ $a_\nu \in \{-1, \ 0, +1\}$ als auch redundant ⇒ statistische Bindungen zwischen den $a_\nu$.
Eigenschaften des AMI-Codes
Die einzelnen Pseudoternärcodes unterscheiden sich in den Parametern $N_{\rm C}$ und $K_{\rm C}$.
Der bekannteste Vertreter ist der Bipolarcode erster Ordnung mit den Codeparametern $N_{\rm C} = 1$ und $K_{\rm C} = 1$, der auch unter der Bezeichnung AMI–Code (von: Alternate Mark Inversion) bekannt ist. Dieser wird zum Beispiel bei ISDN (Integrated Services Digital Networks) auf der so genannten $S_0$–Schnittstelle eingesetzt.
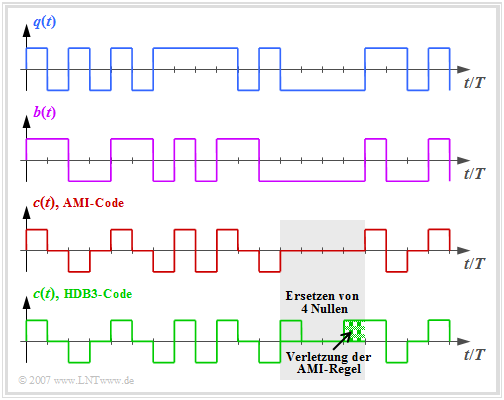
Die Grafik zeigt oben das binäre Quellensignal $q(t)$. Im zweiten und dritten Diagramm sind dargestellt:
- das ebenfalls binäre Signal $b(t)$ nach dem Vorcodierer, und
- das Codersignal $c(t) = s(t)$ des AMI–Codes.
Man erkennt das einfache AMI–Codierprinzip:
- Jeder Binärwert „–1” von $q(t)$ ⇒ Symbol $\rm L$ wird durch den ternären Amplitudenkoeffizienten $a_\nu = 0$ codiert.
- Der Binärwert „+1” von $q(t)$ ⇒ Symbol $\rm H$ wird alternierend mit $a_\nu = +1$ und $a_\nu = -1$ dargestellt.
Damit wird sichergestellt, dass im AMI–codierten Signal keine langen „+1”– bzw. „–1”–Sequenzen enthalten sind, was bei einem gleichsignalfreien Kanal zu Problemen führen würde.
Dagegen ist das Auftreten langer Nullfolgen durchaus möglich, bei denen über einen längeren Zeitraum keine Taktinformation übertragen wird.
Um dieses zweite Problem zu vermeiden, wurden einige modifizierte AMI–Codes entwickelt, zum Beispiel der B6ZS–Code und der HDB3–Code:
- Beim HDB3–Code (grüne Kurve in obiger Grafik) werden vier aufeinanderfolgende Nullen im AMI–codierten Signal durch eine Teilsequenz ersetzt, die die AMI–Codierregel verletzt.
- Im grau hinterlegten Bereich ist dies die Folge „+ 0 0 +”, da das letzte Symbol vor der Ersetzung ein „Minus” war.
- Damit ist beim HDB3–Code die Anzahl aufeinanderfolgender Nullen auf $3$ begrenzt und beim B6ZS–Code auf $5$.
- Der Decoder erkennt diese Codeverletzung und ersetzt „+ 0 0 +” wieder durch „0 0 0 0”.
Leistungsdichtespektrum des AMI-Codes
Der Frequenzgang des linearen Codiernetzwerks eines Pseudoternärcodes lautet allgemein:
- $$H_{\rm C}(f) = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot {\rm e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi\hspace{0.03cm}\cdot \hspace{0.03cm}f \hspace{0.03cm}\cdot \hspace{0.03cm} N_{\rm C}\hspace{0.03cm}\cdot \hspace{0.03cm}T} \big] ={1}/{2} \cdot \big [1 - K \cdot {\rm e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} \alpha} \big ]\hspace{0.05cm}.$$
Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten $(K$ und $\alpha$ sind Abkürzungen entsprechend obiger Gleichung$)$:
- $$ {\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = \frac{\big [1 - K \cos (\alpha) + {\rm j}\cdot K \sin (\alpha) \big ] \big [1 - K \cos (\alpha) - {\rm j}\cdot K \sin (\alpha) \big ] }{4} = \text{...} = {1}/{4} \cdot \big [2 - 2 \cdot K \cdot \cos (\alpha) \big ] $$
- $$ \Rightarrow \hspace{0.3cm}{\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ] \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} \varphi_a(\lambda \cdot T)\hspace{0.05cm}.$$
Insbesondere erhält man für das Leistungsdichtespektrum (LDS) des AMI–Codes $(N_{\rm C} = K_{\rm C} = 1)$:
- $${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 (\pi f T)\hspace{0.05cm}.$$
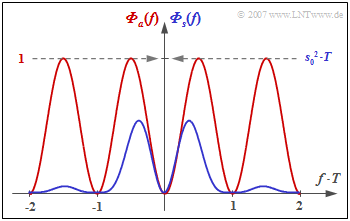
Die Grafik zeigt
- das LDS ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten (rote Kurve), und
- das LDS ${\it \Phi}_s(f)$ des gesamten Sendesignals (blau), gültig für NRZ–Rechteckimpulse.
Man erkennt aus dieser Darstellung
- die Gleichsignalfreiheit des AMI–Codes, da ${\it \Phi}_a(f = 0) = {\it \Phi}_s(f = 0) = 0$ ist,
- die Leistung $P_{\rm S} = s_0^2/2$ des AMI–codierten Sendesignals (Integral über ${\it \Phi}_s(f)$ von $- \infty$ bis $+\infty$).
Hinweise:
- Das LDS von HDB3– und B6ZS–Code weicht von dem des AMI–Codes nur unwesentlich ab.
- Die hier behandelte Thematik können Sie sich mit dem interaktiven Applet Signale, AKF und LDS der Pseudoternärcodes verdeutlichen.
Eigenschaften des Duobinärcodes
Der Duobinärcode ist durch die Codeparameter $N_{\rm C} = 1$ und $K_{\rm C} = -1$ festgelegt. Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten bzw. für das LDS des Sendesignals:
- $${\it \Phi}_a(f) ={1}/{2} \cdot \big [1 + \cos (2\pi f T)\big ] = \cos^2 (\pi f T)\hspace{0.05cm},$$
- $$ {\it \Phi}_s(f) = s_0^2 \cdot T \cdot \cos^2 (\pi f T)\cdot {\rm si}^2 (\pi f T)= s_0^2 \cdot T \cdot {\rm si}^2 (2 \pi f T) \hspace{0.05cm}.$$
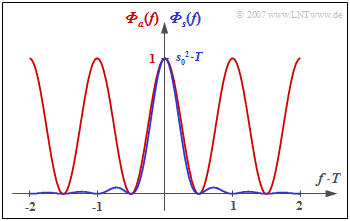
Die Grafik zeigt das Leistungsdichtespektrum
- der Amplitudenkoeffizienten ⇒ ${\it \Phi}_a(f)$ als rote Kurve,
- des gesamten Sendsignals ⇒ ${\it \Phi}_s(f)$ als blaue Kurve.
In der zweiten Grafik sind die Signale $q(t)$, $b(t)$ und $c(t) = s(t)$ skizziert. Wir verweisen hier wieder auf das Applet Signale, AKF und LDS der Pseudoternärcodes, das auch die Eigenschaften des Duobinärcodes verdeutlicht.
Aus diesen Darstellungen geht hervor:
- Beim Duobinärcode können beliebig viele Symbole mit gleicher Polarität („+1” bzw. „–1”) direkt aufeinanderfolgen.
- Deshalb gilt ${\it \Phi}_a(f = 0)=1$ und ${\it \Phi}_s(f = 0) = 1/2 \cdot s_0^2 \cdot T$.
- Dagegen tritt beim Duobinärcode die alternierende Folge „ ... , +1, –1, +1, –1, +1, ... ” nicht auf, die hinsichtlich Impulsinterferenzen besonders störend ist.
- Deshalb gilt beim Duobinärcode: ${\it \Phi}_s(f = 1/(2T) = 0$.
- Das Leistungsdichtespektrum ${\it \Phi}_s(f)$ des pseudoternären Duobinärcodes ist identisch mit dem LDS bei redundanzfreier Binärcodierung mit halber Rate $($Symboldauer $2T)$.
Fehlerwahrscheinlichkeit der Pseudoternärcodes
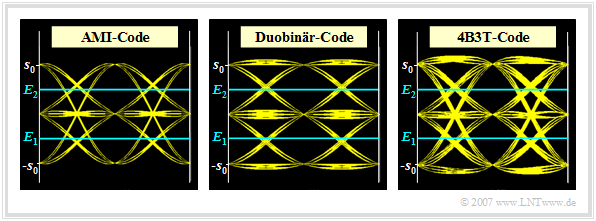
Die Grafik zeigt die Augendiagramme (ohne Rauschen) bei Verwendung
- von AMI–Code (links)
- und Duobinärcode (Mitte)
- im Vergleich zum 4B3T–Code (rechts).
Es gelten die gleichen Voraussetzungen wie auf der Seite Fehlerwahrscheinlichkeit der 4B3T-Codes.
Insbesondere: Cosinus–Rolloff–Charakteristik des Gesamtfrequenzgangs (von Sender und Empfänger) mit dem Rolloff–Faktor $r = 0.8$.
Die Ergebnisse sind wie folgt zu interpretieren:
- Man erkennt in der linken Grafik, dass beim AMI–Code die horizontalen Linien bei $+s_0$ und $-s_0$ fehlen (Gleichsignalfreiheit!), während beim Duobinärcode (mittlere Grafik) keine Übergänge von $+s_0$ auf $-s_0$ (und umgekehrt) möglich sind.
- Beim 4B3T–Code erkennt man im Augendiagramm deutlich mehr Linien als bei den beiden linken Bildern. Der redundanzfreie Ternärcode würde nahezu das gleiche Ergebnis liefern.
- Auf der oben zitierten Seite wurde die Symbolfehlerwahrscheinlichkeit des 4B3T–Codes für die Leistungskenngröße $10 \cdot \lg \hspace{0.05cm}(s_0^2 \cdot T/N_0) = 13 \ \rm dB$ (gültig für Spitzenwertbegrenzung!) wie folgt berechnet:
- $${ \sigma_d}/{s_0} = 0.145 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm S} = {4}/{3} \cdot {\rm Q} \left( \frac{s_0/2}{ \sigma_d} \right) \approx {4}/{3} \cdot {\rm Q} \left( 3.45 \right) = 3.7 \cdot 10^{-4} \hspace{0.05cm}.$$
- Bei Verwendung eines Pseudoternärcodes ergibt sich eine größere Fehlerwahrscheinlichkeit, weil hier der Rauscheffektivwert gegenüber der redundanzfreien Binärcodierung nicht verringert wird:
- $${ \sigma_d}/{s_0} = 0.167 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm S} = {4}/{3} \cdot {\rm Q} \left( \frac{s_0/2}{ \sigma_d} \right) \approx {4}/{3} \cdot {\rm Q} \left( 3 \right) = 1.8 \cdot 10^{-3} \hspace{0.05cm}.$$
- Bei Erfüllung der Nyquistbedingung unterscheiden sich der AMI– und der Duobinärcode trotz völlig unterschiedlicher Augendiagramme nicht hinsichtlich der Fehlerwahrscheinlichkeit.
- Wie aber im Abschnitt Augenöffnung bei den Pseudoternärcodes noch gezeigt werden wird, ist das Fehlerverhalten der beiden Codes immer dann extrem unterschiedlich, wenn Impulsinterferenzen eine Rolle spielen.
Aufgaben zum Kapitel
Aufgabe 2.7Z: Leistungsdichtespektren der Pseudoternärcodes
Aufgabe 2.8: Vergleich von Binärcode, AMI-Code und 4B3T-Code