Aufgaben:Aufgabe 1.1: Sendegrundimpulse

• Zurück zum Buch

Betrachtete Sendegrundimpulse

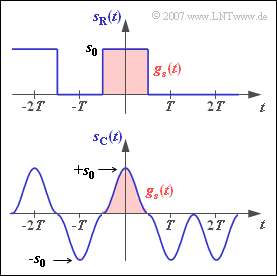
Wir untersuchen in dieser Aufgabe die zwei in der Grafik dargestellten Sendesignale  $s_{\rm R}(t)$  und  $s_{\rm C}(t)$  mit Rechteck– bzw.  $\cos^2$–Sendegrundimpuls. Insbesondere sollen für die jeweiligen Impulse  $g_s(t)$  folgende Kenngrößen berechnet werden:

• die äquivalente Impulsdauer von  $g_s(t)$:

$$\Delta t_{\rm S} = \frac {\int ^{+\infty} _{-\infty} \hspace{0.15cm} g_s(t)\,{\rm d}t}{{\rm Max} \hspace{0.05cm}[g_s(t)]} \hspace{0.05cm},$$

• die Energie des Sendegrundimpulses  $g_s(t)$:

$$E_g = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t \hspace{0.05cm},$$

• die Leistung des Sendesignals  $s(t)$:

$$P_{\rm S} = \lim_{T_{\rm M} \to \infty} \frac{1}{+T_{\rm M}} \cdot \int^{+T_{\rm M}/2} _{-T_{\rm M}/2} s^2(t)\,{\rm d}t \hspace{0.05cm}.$$

Gehen Sie bei Ihren Berechnungen stets davon aus, dass die beiden möglichen Amplitudenkoeffizienten gleichwahrscheinlich sind und dass der Abstand zwischen benachbarten Symbolen  $T = 1 \ \rm µ s$  beträgt. Dies entspricht einer Bitrate von  $R = 1 \ \rm Mbit/s$.

• Der (positive) Maximalwert des Sendesignals ist in beiden Fällen gleich

$$s_0 = \sqrt{0.5\, {\rm W}} \hspace{0.05cm}.$$

• Unter der Annahme, dass der Sender mit einem Widerstand von  $50\ \rm Ω$  abgeschlossen ist, entspricht dies dem folgenden Spannungswert:

$$s_0 = \sqrt{0.5\, {\rm W}} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Systemkomponenten eines Basisbandübertragungssystems.
• Bezug genommen wird insbesondere auf den Abschnitt  Kenngrößen des digitalen Senders.

• Gegeben ist das folgende unbestimmte Integral:

$$\int \cos^4(a x)\,{\rm d}x = \frac{3}{8} \cdot x + \frac{1}{4a} \cdot \sin(2 a x)+ \frac{1}{32a} \cdot \sin(4 a x)\hspace{0.05cm}.$$

Fragebogen

1

Handelt es sich bei $s_{\rm R}(t)$ und $s_{\rm C}(t)$ um unipolare oder bipolare Signale?

	$s_{\rm R}(t)$  ist ein bipolares Signal und  $s_{\rm C}(t)$  ein unipolares.
	$s_{\rm C}(t)$  ist ein bipolares Signall und  $s_{\rm R}(t)$  ein unipolares.

2

Wie groß ist die äquivalente Impulsdauer  $\Delta t_{\rm S}$, normiert auf die Symboldauer  $T$?

$\text{beim Signal}\ \ s_{\rm R}(t) \text{:} \ \ \Delta t_{\rm S}/T \ = \ $

$\text{beim Signal}\ \ s_{\rm C}(t) \text{:} \ \ \Delta t_{\rm S}/T \ = \ $

3

Wie groß ist die Energie des rechteckförmigen Sendegrundimpulses??

$E_g \ = \ $ $\ \cdot 10^{-6}\ \rm Ws$

4

Wie groß ist die Leistung des rechteckförmigen Sendesignals  $s_{\rm R}(t)$?

$P_{\rm S} \ = \ $ $\ \rm W$

5

Wie groß ist die Energie des  $\cos^2$–Sendegrundimpulses?

$E_g \ = \ $ $\ \cdot 10^{-6}\ \rm Ws$

6

Wie groß ist die Leistung des Sendesignals  $s_{\rm C}(t)$?

$P_{\rm S} \ = \ $ $\ \rm W$

Musterlösung

Musterlösung

(1)  Richtig ist der Lösungsvorschlag 2:

• In beiden Fällen kann das Sendesignal in folgender Form dargestellt werden:

$$s(t) = \sum_{(\nu)} a_\nu \cdot g_s ( t - \nu \cdot T)$$

• Beim Signal $s_{\rm R}(t)$ sind die Amplitudenkoeffizienten $a_ν$ entweder $0$ oder $1$. Es liegt also ein unipolares Signal vor.
• Beim bipolaren Signal $s_{\rm R}(t)$ gilt dagegen $a_ν ∈ \{–1, +1\}$.

(2)  Das Signal $s_{\rm R}(t)$ ist NRZ–rechteckförmig.

• Dementsprechend sind sowohl die absolute Impulsdauer $T_{\rm S}$ als auch die äquivalente Impulsdauer $\Delta t_{\rm S}$ gleich der Symboldauer $T$:

$$T_{\rm S} / T = 1\hspace{0.05cm},\hspace{0.3cm}\Delta t_{\rm S} / T \hspace{0.1cm}\underline{ = 1 }\hspace{0.05cm}.$$

• Der Sendegrundimpuls für das Signal $s_{\rm C}(t)$ lautet:

$$g_s(t) = \left\{ \begin{array}{c} s_0 \cdot \cos^2(\pi \cdot \frac{t}{T}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} -T/2 \le t \le +T/2 \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}. \\ \end{array}$$

• Aus der Grafik auf der Angabenseite erkennt man, dass für den $\cos^2$–Impuls folgende Werte gelten:

$$T_{\rm S} / T = 1\hspace{0.05cm},\hspace{0.3cm}\Delta t_{\rm S} / T \hspace{0.1cm}\underline{ = 0.5} \hspace{0.05cm}.$$

(3)  Für die Energie des Rechteckimpulses gilt:

$$E_g = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t = s_0^2 \cdot T = 0.5\, {\rm W} \cdot 1\, {\rm µ s} \hspace{0.1cm}\underline{= 0.5 \cdot 10^{-6}\, {\rm Ws}}\hspace{0.05cm}.$$

(4)  Bei einem bipolaren Rechtecksignal würde gelten:

$$s_{\rm R}^2(t)= s_0^2 = {\rm const.} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_s = s_0^2 \cdot \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int ^{T_{\rm M}/2} _{-T_{\rm M}/2} \,{\rm d}t = s_0^2 \hspace{0.05cm}.$$

• Da das Signal $s_{\rm R}(t)$ hier jedoch unipolar ist, gilt in der Hälfte der Zeit $s_{\rm R}(t)= 0$. Somit ergibt sich:

$$P_{\rm S} = {1}/{2} \cdot s_0^2 \hspace{0.1cm}\underline{= 0.25 \,{\rm W}} \hspace{0.05cm}.$$

(5)  Für die Energie des $\cos^2$–Impulses gilt:

$$E_g = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t = 2 \cdot s_0^2 \cdot \int^{T/2} _{0} \cos^4(\pi \cdot {t}/{T})\,{\rm d}t \hspace{0.05cm}.$$

• Hierbei ist die unter Punkt (3) hergeleitete Formel und die Symmetrie von $g_s(t)$ um den Zeitpunkt $t = 0$ berücksichtigt.
• Das Integral ist bei der Aufgabenbeschreibung angegeben, wobei $a = π/T$ zu setzen ist:

$$E_g = 2 \cdot s_0^2 \cdot \left [ \frac{3}{8} \cdot t + \frac{T}{4\pi} \cdot \sin(2 \pi \frac{t}{T})+ \frac{T}{32\pi} \cdot \sin(4 \pi \frac{t}{T})\right ]_{0}^{T/2}\hspace{0.05cm}.$$

• Die untere Grenze $t = 0$ liefert stets das Ergebnis $0$. Hinsichtlich der oberen Grenze ergibt sich nur für den ersten Term ein von $0$ verschiedenes Ergebnis. Also:

$$E_g = 2 \cdot s_0^2 \cdot \frac{3}{8} \cdot \frac{T}{2} = \frac{3}{8} \cdot 5 \cdot 10^{-7}\, {\rm Ws} \hspace{0.1cm}\underline{ = 0.1875 \cdot 10^{-6}\, {\rm Ws}}\hspace{0.05cm}.$$

(6)  Beim bipolaren Signal $s_{\rm C}(t)$ gilt folgender Zusammenhang:

$$P_{\rm S} = \frac{ E_g}{T} = \frac{ 1.875 \cdot 10^{-7}\, {\rm Ws}}{10^{-6}\, {\rm s}}\hspace{0.1cm}\underline{ = 0.1875 \,{\rm W}} \hspace{0.05cm}.$$