Aufgaben:Aufgabe 4.11: C-Programm „akf1”: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 33: | Zeile 33: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Elemente $i$ und $j$ des Hilfsfeldes $H\big[ \ \big]$ werden beim ersten Durchlauf $(z=0)$ zur Berechnung des AKF–Wertes $\varphi(k=6)$ verwendet? <br>Welche Zufallswerte $x_\nu$ stehen in diesen Speicherzellen? | + | {Welche Elemente $i$ und $j$ des Hilfsfeldes $H\big[ \ \big]$ werden <u>beim ersten Durchlauf</u> $(z=0)$ zur Berechnung des AKF–Wertes $\varphi(k=6)$ verwendet? <br>Welche Zufallswerte $x_\nu$ stehen in diesen Speicherzellen? |
|type="{}"} | |type="{}"} | ||
$i \ = \ $ { 0. } | $i \ = \ $ { 0. } | ||
| Zeile 39: | Zeile 39: | ||
| − | {Welche Speicherzelle ${\rm H}\big[\hspace{0.03cm} i \hspace{0.03cm} \big]$ wird nach dem ersten Schleifendurchgang $(z=0)$ mit einer neuen Zufallsgröße $x_\nu$ belegt? <br>Welcher Index $\nu$ wird dabei eingetragen? | + | {Welche Speicherzelle ${\rm H}\big[\hspace{0.03cm} i \hspace{0.03cm} \big]$ wird <u>nach dem ersten Schleifendurchgang</u> $(z=0)$ mit einer neuen Zufallsgröße $x_\nu$ belegt? <br>Welcher Index $\nu$ wird dabei eingetragen? |
|type="{}"} | |type="{}"} | ||
$i \ = \ $ { 0. } | $i \ = \ $ { 0. } | ||
| Zeile 57: | Zeile 57: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Mit $z= 0$ und $k=6$ ergibt sich gemäß dem Programm: $\underline{i= 0}$ und $\underline{j= 6}$. | + | [[Datei:P_ID417__Sto_A_4_11_b.png|right|frame|Zur numerischen AKF-Berechnung]] |
| − | <br>Die entsprechenden Speicherinhalte sind ${ | + | <br> |
| + | '''(1)''' Mit $z= 0$ und $k=6$ ergibt sich gemäß dem Programm: $\underline{i= 0}$ und $\underline{j= 6}$. | ||
| + | <br>Die entsprechenden Speicherinhalte sind ${H}\big[\hspace{0.03cm} 0 \hspace{0.03cm}\big] = x_1$ und ${H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big] = x_7$. | ||
| − | '''(2)''' In das Feld ${ | + | |
| + | '''(2)''' In das Feld ${H}\big[\hspace{0.03cm} 0 \hspace{0.03cm}\big]$ wird nun die Zufallsgröße $x_{12}$ eingetragen: | ||
:$$\text{Speicherzelle }\underline{i= 0},\hspace{1cm}\text{Folgenindex }\underline{\nu= 12}.$$ | :$$\text{Speicherzelle }\underline{i= 0},\hspace{1cm}\text{Folgenindex }\underline{\nu= 12}.$$ | ||
| − | |||
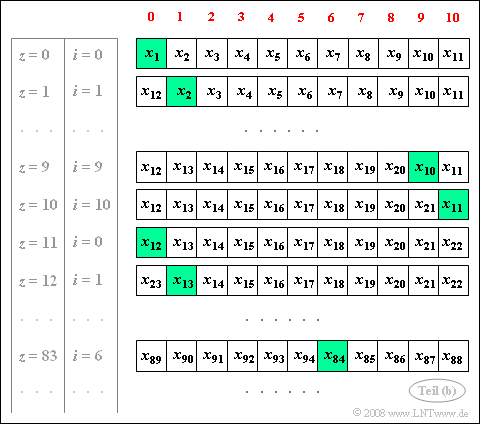
| − | + | '''(3)''' Die Grafik zeigt die Belegung des Hilfsfeldes mit den Zufallswerten $x_\nu$. | |
| − | *Jeweils grün hinterlegt ist die Speicherzelle ${ | + | *Jeweils grün hinterlegt ist die Speicherzelle ${H}\big[\hspace{0.03cm} i \hspace{0.03cm}\big]$. In diesen Speicherplatz wird jeweils am Ende der Schleife (Zeile 18) die neue Zufallsgröße eingetragen. |
| − | *Für $z= 83$ und $K=6$ ergibt sich $\underline{i= 83 \mod \ 11 = 6} | + | *Für $z= 83$ und $K=6$ ergibt sich |
| − | *In | + | :$$\underline{i= 83 \mod \ 11 = 6},\hspace{1cm} \underline{j= (i+k) \mod \ 11 = 1}.$$ |
| − | *Am Ende des Schleifendurchlaufs $z= 83$ wird in ${ | + | *Schleifendurchlaufs $z= 83$: In der Speicherzelle ${H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big]$ steht die Zufallsgröße $x_{84}$ und in der Speicherzelle ${H}\big[\hspace{0.03cm} 1 \hspace{0.03cm}\big]$die Zufallsgröße $x_{90}$. |
| + | *Am Ende des Schleifendurchlaufs $z= 83$ wird in ${H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big]$ der Inhalt $x_{84}$ durch $x_{95}$ ersetzt. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 18. August 2018, 16:02 Uhr
Sie sehen nebenstehend das C–Programm „akf1” zur Berechnung der diskreten AKF-Werte $\varphi_x(k)$ mit dem Index $k = 0$, ... , $l$. Hierzu ist Folgendes zu bemerken:
- Der an das Programm übergebene Long–Wert sei $l = 10$. Die AKF-Werte $\varphi_x(0)$, ... , $\varphi_x(10)$ werden mit dem Float-Feld $\rm AKF\big[ \ \big]$ an das aufrufende Programm zurückgegeben. In den Zeilen 7 und 8 des rechts anggebenen Programms wird dieses Feld mit Nullen vorbelegt.
- Die zu analysierenden Zufallsgrößen $x_\nu$ werden mit der Float-Funktion $x( \ )$ erzeugt (siehe Zeile 4). Diese Funktion wird insgesamt $N + l + 1 = 10011$ mal aufgerufen (Zeile 9 und 18).
- Im Gegensatz zu dem im Theoriteil angegebenen Algorithmus, der im Programm „akf2” von Aufgabe 4.11Z direkt umgesetzt ist, benötigt man hier ein Hilfsfeld $H\big[ \ \big]$ mit nur $l + 1 = 11$ Speicherelementen.
- Vor Beginn des eigentlichen Berechnungsalgorithmus (Zeile 11 bis 21) stehen in den elf Speicherzellen von $H\big[ \ \big]$ die Zufallswerte $x_1$, ... , $x_{11}$.
- Die äußere Schleife mit der Laufvariablen $z$ (rot markiert) wird $N$-mal durchlaufen.
- In der inneren Schleife (weiß markiert) werden mit dem Laufindex $k = 0$, ... , $l$ alle Speicherzellen des Feldes ${\rm AKF}\big[\hspace{0.03cm} k \hspace{0.03cm} \big]$ um den Betrag $x_\nu \cdot x_{\nu+k}$ erhöht.
- In den Zeilen 22 und 23 werden schließlich alle AKF–Werte durch die Anzahl $N$ dividiert.
Hinweise:
- Die Aufgabe gehört zum Kapitel Autokorrelationsfunktion.
- Bezug genommen wird insbesondere auf die Seite Numerische AKF-Ermittlung.
Fragebogen
Musterlösung
(1) Mit $z= 0$ und $k=6$ ergibt sich gemäß dem Programm: $\underline{i= 0}$ und $\underline{j= 6}$.
Die entsprechenden Speicherinhalte sind ${H}\big[\hspace{0.03cm} 0 \hspace{0.03cm}\big] = x_1$ und ${H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big] = x_7$.
(2) In das Feld ${H}\big[\hspace{0.03cm} 0 \hspace{0.03cm}\big]$ wird nun die Zufallsgröße $x_{12}$ eingetragen:
- $$\text{Speicherzelle }\underline{i= 0},\hspace{1cm}\text{Folgenindex }\underline{\nu= 12}.$$
(3) Die Grafik zeigt die Belegung des Hilfsfeldes mit den Zufallswerten $x_\nu$.
- Jeweils grün hinterlegt ist die Speicherzelle ${H}\big[\hspace{0.03cm} i \hspace{0.03cm}\big]$. In diesen Speicherplatz wird jeweils am Ende der Schleife (Zeile 18) die neue Zufallsgröße eingetragen.
- Für $z= 83$ und $K=6$ ergibt sich
- $$\underline{i= 83 \mod \ 11 = 6},\hspace{1cm} \underline{j= (i+k) \mod \ 11 = 1}.$$
- Schleifendurchlaufs $z= 83$: In der Speicherzelle ${H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big]$ steht die Zufallsgröße $x_{84}$ und in der Speicherzelle ${H}\big[\hspace{0.03cm} 1 \hspace{0.03cm}\big]$die Zufallsgröße $x_{90}$.
- Am Ende des Schleifendurchlaufs $z= 83$ wird in ${H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big]$ der Inhalt $x_{84}$ durch $x_{95}$ ersetzt.