Aufgaben:Aufgabe 1.7Z: BARBARA-Generator

• Zurück zum Buch

BARBARA-Generator

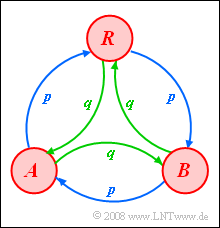
Betrachtet wird hier ein ternärer Zufallsgenerator mit den Symbolen $A$, $B$ und $R$, der durch eine homogene und stationäre Markovkette erster Ordnung beschrieben werden kann.

Die Übergangswahrscheinlichkeiten können dem skizzierten Markovdiagramm entnommen werden. Für die ersten drei Teilaufgaben soll stets $p = 1/4$ gelten.

Hinweis:

• Die Aufgabe gehört zum Kapitel Markovketten.

Fragebogen

1

Welche der nachfolgenden Aussagen sind zutreffend?

	Die Werte von $p > 0$ und $q < 1$ sind weitgehend frei wählbar.
	Für die Übergangswahrscheinlichkeiten muss gelten:   $p + q = 1$.
	Alle Symbole haben gleiche ergodische Wahrscheinlichkeiten.
	Es gilt hier: ${\rm Pr}(A) = 1/2, \; {\rm Pr}(B) = 1/3, \; {\rm Pr}(R) = 1/6$.

2

Wie groß sind die bedingten Wahrscheinlichkeiten $p_{\rm A}$, $p_{\rm B}$ und $p_{\rm C}$, dass im Zeitbereich zwischen $ν+1$ und $ν+7$ die Sequenz $\rm BARBARA$ ausgegeben wird, wenn man sich zum Zeitpunkt $ν$ im Zustand $A$, $B$ bzw. $R$ befindet? Es gelte $p = 1/4$.

$p_{\rm A} \ = \ $ $\ \cdot 10^{-3}$

$p_{\rm B} \ = \ $ $\ \cdot 10^{-3}$

$p_{\rm C} \ = \ $ $\ \cdot 10^{-3}$

3

Wie groß ist die Wahrscheinlichkeit insgesamt, dass der Generator zu sieben aufeinanderfolgenden Zeitpunkten die Sequenz $BARBARA$ ausgibt. Es gelte weiter $(p = 1/4)$?

$p = 1/4\hspace{-0.1cm}: \hspace{0.3cm}{\rm Pr}(BARBARA)\ = \ $ $\ \cdot 10^{-3}$

4

Wie ist der Parameter $p_{\rm opt}$ zu wählen, damit $Pr(BARBARA)$ möglichst groß wird? Welche Wahrscheinlichkeit ergibt sich damit für BARBARA?

$p_{\rm opt} \ = \ $

$p = p_{\rm opt}\hspace{-0.1cm}: \hspace{0.3cm}{\rm Pr}(BARBARA)\ = \ $ $\ \cdot 10^{-3}$

Musterlösung

Musterlösung

(1)  Richtig sind der zweite und der dritte Lösungsvorschlag:

• Die Summe aller abgehenden Pfeile muss immer $1$ sein. Deshalb gilt $q = 1 - p$.
• Aufgrund der Symmetrie des Markovdiagramms sind die ergodischen Wahrscheinlichkeiten alle gleich:

$${\rm Pr}(A) ={\rm Pr}(B) ={\rm Pr}(R) = 1/3.$$

(2)  Wenn man zum Zeitpunkt $\nu$ im Zustand $B$ ist, ist für den Zeitpunkt $\nu+1$ wegen ${\rm Pr}(B\hspace{0.05cm}|\hspace{0.05cm}B) = 0$ der Zustand $B$ nicht möglich. Man scheitert hier bereits beim Anfangsbuchstaben $B$:

$$p_{\rm B} \; \underline{ =0}.$$

Für die Berechnung von $p_{\rm A}$ ist zu beachten: Ausgehend von $A$ geht man im Markovdiagramm zunächst zu $B$ (mit der Wahrscheinlichkeit $q$), dann fünfmal im Uhrzeigersinn (jeweils mit der Wahrscheinlichkeit $p$) und schließlich noch von $R$ nach $A$ (mit der Wahrscheinlichkeit $q$). Das bedeutet:

$$p_{\rm A} = q^2 \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 = 3^2 / 4^7 \hspace{0.15cm}\underline {\approx 0.549 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$

In ähnlicher Weise erhält man:

$$p_{\rm R} = q \hspace{0.05cm}\cdot \hspace{0.05cm} p^6 = 3 / 4^7 \hspace{0.15cm}\underline {\approx 0.183 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$

(3)  Durch Mittelung über die bedingten Wahrscheinlichkeiten erhält man:

$${\rm Pr}(BARBARA) = p_{\rm A} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm}p_{\rm B} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm Pr}(B) \hspace{0.1cm} + \hspace{0.1cm}p_{\rm R} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm Pr}(R).$$

Dies führt zum Ergebnis:

$${\rm Pr}(BARBARA) = {1}/{3} \cdot \left( q^2 \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 \hspace{0.1cm} +\hspace{0.1cm}0 \hspace{0.1cm} +\hspace{0.1cm}q \hspace{0.05cm}\cdot \hspace{0.05cm} p^6 \right) = \frac{q \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 }{3} \cdot (p+q) = \hspace{-0.15cm} \frac{q \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 }{3} \hspace{0.15cm}\underline { \approx 0.244 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$

(4)  Die im Punkt (3) berechnete Wahrscheinlichkeit lautet $p^5 \cdot (1-p)/3$, wobei $q= 1-p$ berücksichtigt ist. Durch Nullsetzen des Differentials erhält man die Bestimmungsgleichung:

$$5 \cdot p^4 - 6 \cdot p^5 = 0 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm opt} = 5/6 \hspace{0.15cm}\underline { \approx \rm 0.833}.$$

Damit ergibt sich ein gegenüberder Teilaufgabe (3) etwa um den Faktor 90 größerer Wert:

$${\rm Pr}(BARBARA) \hspace{0.15cm}\underline { \approx 22 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$