Aufgaben:Aufgabe 3.7: Hochpass-Impulsantwort: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 3.7 Hochpass-Impulsantwort nach Aufgabe 3.7: Hochpass-Impulsantwort) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1787__LZI_A_3_7.png|right|Hochpass zweiter Ordnung]] | + | [[Datei:P_ID1787__LZI_A_3_7.png|right|frame|Hochpass zweiter Ordnung]] |
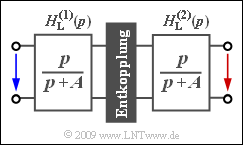
Wir gehen von der nebenstehend skizzierten Anordnung aus. Die Übertragungsfunktionen der beiden identischen Hochpässe lauten: | Wir gehen von der nebenstehend skizzierten Anordnung aus. Die Übertragungsfunktionen der beiden identischen Hochpässe lauten: | ||
| − | $$H_{\rm L}^{(1)}(p) = H_{\rm L}^{(2)}(p) =\frac{p}{p+A} | + | :$$H_{\rm L}^{(1)}(p) = H_{\rm L}^{(2)}(p) =\frac{p}{p+A} |
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
Da die Vierpole durch einen Trennverstärker widerstandsmäßig entkoppelt sind, lässt sich für die Gesamtübertragungsfunktion schreiben: | Da die Vierpole durch einen Trennverstärker widerstandsmäßig entkoppelt sind, lässt sich für die Gesamtübertragungsfunktion schreiben: | ||
| − | $$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) | + | :$$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) |
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
Gleichzeitig ist bekannt, dass folgende Gleichung gültig ist: | Gleichzeitig ist bekannt, dass folgende Gleichung gültig ist: | ||
| − | $$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4} | + | :$$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4} |
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
Stellt man diese Funktion in Pol–Nullstellen–Form dar, so wird sich herausstellen, dass hier die Anzahl der Nullstellen ($Z$) gleich der Anzahl der Pole ($N$) ist. Eine direkte Anwendung des Residuensatzes ist hier deshalb nicht möglich. | Stellt man diese Funktion in Pol–Nullstellen–Form dar, so wird sich herausstellen, dass hier die Anzahl der Nullstellen ($Z$) gleich der Anzahl der Pole ($N$) ist. Eine direkte Anwendung des Residuensatzes ist hier deshalb nicht möglich. | ||
| Zeile 19: | Zeile 19: | ||
\hspace{0.05cm}$ | \hspace{0.05cm}$ | ||
vorgenommen werden. Damit gilt für die Impulsantwort: | vorgenommen werden. Damit gilt für die Impulsantwort: | ||
| − | $$h(t) = \delta(t)- h\hspace{0.03cm}'(t) | + | :$$h(t) = \delta(t)- h\hspace{0.03cm}'(t) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Bezüglich $H_{\rm L}'(p)$ gilt $Z' < N'$. Somit kann der kontinuierliche Anteil $h'(t)$ der Impulsantwort wieder mit dem Residuensatz ermittelt werden. | Bezüglich $H_{\rm L}'(p)$ gilt $Z' < N'$. Somit kann der kontinuierliche Anteil $h'(t)$ der Impulsantwort wieder mit dem Residuensatz ermittelt werden. | ||
| + | |||
| + | |||
| + | |||
| Zeile 29: | Zeile 32: | ||
*Das Residium eines $l$–fachen Pols $p_{\rm x}$ innerhalb der Funktion $H_{\rm L}(p)$ lautet: | *Das Residium eines $l$–fachen Pols $p_{\rm x}$ innerhalb der Funktion $H_{\rm L}(p)$ lautet: | ||
:$${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} | :$${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} | ||
| − | \hspace{0. | + | \hspace{0.03cm}\{H_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= |
\frac{1}{(l-1)!}\cdot \frac{{\rm d}^{\hspace{0.05cm}l-1}}{{\rm d}p^{\hspace{0.05cm}l-1}}\hspace{0.15cm} | \frac{1}{(l-1)!}\cdot \frac{{\rm d}^{\hspace{0.05cm}l-1}}{{\rm d}p^{\hspace{0.05cm}l-1}}\hspace{0.15cm} | ||
\left \{H_{\rm L}(p)\cdot (p - p_{\rm x})^{\hspace{0.05cm}l} \cdot {\rm e}^{\hspace{0.05cm}p | \left \{H_{\rm L}(p)\cdot (p - p_{\rm x})^{\hspace{0.05cm}l} \cdot {\rm e}^{\hspace{0.05cm}p | ||
| Zeile 47: | Zeile 50: | ||
{Stellen Sie $H_{\rm L}(p)$ in Pol–Nullstellen–Form dar. Wieviele Nullstellen ($Z$) und Pole ($N$) gibt es? Wie groß ist der konstante Faktor $K$? | {Stellen Sie $H_{\rm L}(p)$ in Pol–Nullstellen–Form dar. Wieviele Nullstellen ($Z$) und Pole ($N$) gibt es? Wie groß ist der konstante Faktor $K$? | ||
|type="{}"} | |type="{}"} | ||
| − | $Z \ =$ { 2 | + | $Z \hspace{0.28cm} = \ $ { 2 } |
| − | $N \ =$ { 2 | + | $N \hspace{0.2cm} = \ $ { 2 } |
| − | $K \ =$ { 1 | + | $K \hspace{0.2cm} = \ $ { 1 } |
{Wie groß ist der Parameter $A$ der beiden Teilvierpolen? | {Wie groß ist der Parameter $A$ der beiden Teilvierpolen? | ||
|type="{}"} | |type="{}"} | ||
| − | $A \ = $ { 0.5 3% } | + | $A \ = \ $ { 0.5 3% } |
| Zeile 66: | Zeile 69: | ||
{Berechnen Sie die Zeitfunktion $h'(t)$. Welche Zahlenwerte ergeben sich für die angegebenen Zeitpunkte? | {Berechnen Sie die Zeitfunktion $h'(t)$. Welche Zahlenwerte ergeben sich für die angegebenen Zeitpunkte? | ||
|type="{}"} | |type="{}"} | ||
| − | $h'(t = 0) \ =$ { 1 3% } | + | $h'(t = 0) \ = \ $ { 1 3% } |
| − | $h'(t = 1) \ =$ { 0.455 3% } | + | $h'(t = 1) \ = \ $ { 0.455 3% } |
| − | $h'(t → ∞)\ = $ { 0. } | + | $h'(t → ∞)\ = \ $ { 0. } |
Version vom 17. März 2018, 15:47 Uhr
Wir gehen von der nebenstehend skizzierten Anordnung aus. Die Übertragungsfunktionen der beiden identischen Hochpässe lauten:
- $$H_{\rm L}^{(1)}(p) = H_{\rm L}^{(2)}(p) =\frac{p}{p+A} \hspace{0.05cm} .$$
Da die Vierpole durch einen Trennverstärker widerstandsmäßig entkoppelt sind, lässt sich für die Gesamtübertragungsfunktion schreiben:
- $$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) \hspace{0.05cm} .$$
Gleichzeitig ist bekannt, dass folgende Gleichung gültig ist:
- $$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4} \hspace{0.05cm} .$$
Stellt man diese Funktion in Pol–Nullstellen–Form dar, so wird sich herausstellen, dass hier die Anzahl der Nullstellen ($Z$) gleich der Anzahl der Pole ($N$) ist. Eine direkte Anwendung des Residuensatzes ist hier deshalb nicht möglich.
Um die Zeitfunktion $h(t)$ berechnen zu können, muss vielmehr eine Partialbruchzerlegung entsprechend $H_{\rm L}(p) =1- H_{\rm L}\hspace{-0.05cm}'(p) \hspace{0.05cm}$ vorgenommen werden. Damit gilt für die Impulsantwort:
- $$h(t) = \delta(t)- h\hspace{0.03cm}'(t) \hspace{0.05cm}.$$
Bezüglich $H_{\rm L}'(p)$ gilt $Z' < N'$. Somit kann der kontinuierliche Anteil $h'(t)$ der Impulsantwort wieder mit dem Residuensatz ermittelt werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Laplace–Rücktransformation.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Das Residium eines $l$–fachen Pols $p_{\rm x}$ innerhalb der Funktion $H_{\rm L}(p)$ lautet:
- $${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.03cm}\{H_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= \frac{1}{(l-1)!}\cdot \frac{{\rm d}^{\hspace{0.05cm}l-1}}{{\rm d}p^{\hspace{0.05cm}l-1}}\hspace{0.15cm} \left \{H_{\rm L}(p)\cdot (p - p_{\rm x})^{\hspace{0.05cm}l} \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.05cm} .$$
- Die Ableitung des Produkts $y(x) = f(x) \cdot g(x)$ ist wie folgt gegeben:
- $$\frac{{\rm d}{\hspace{0.05cm}y(x)}}{{\rm d}\hspace{0.05cm}x}= \frac{{\rm d}{\hspace{0.05cm}f(x)}}{{\rm d}\hspace{0.05cm}x}\cdot g(x) + \frac{{\rm d}{\hspace{0.05cm}g(x)}}{{\rm d}\hspace{0.05cm}x}\cdot f(x) \hspace{0.05cm} .$$
Fragebogen
Musterlösung
(2) Die Gesamtübertragungsfunktion lautet entsprechend der Angabe:
$$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) =\frac{p^2}{(p+A)^2}
\hspace{0.05cm} .$$
Ein Vergleich mit dem Ergebnis der Teilaufgabe (1) zeigt, dass $\underline{A = 0.5}$ sein muss.
(3) Ausgehend von der in der Teilaufgabe (1) berechneten Gleichung erhält man
$$H_{\rm L}(p) =\frac{p^2}{p^2 + p +0.25}= \frac{p^2 + p +0.25}{p^2 + p
+0.25}- \frac{p +0.25}{p^2 + p
+0.25}$$
$$ \Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{-0.05cm}'(p) = \frac{p +0.25}{p^2 + p
+0.25}= \frac{p +0.25}{(p
+0.5)^2}
\hspace{0.05cm} .$$
Richtig ist dementsprechend der letzte Lösungsvorschlag.
(4) Bezüglich der Funktion $H_{\rm L}'(p)$ gilt $Z' = 1$, $N' = 2$ und $K' = 1$. Die beiden Pole bei $p_{\rm x} = -0.5$ fallen zusammen, so dass nur ein Residium ermittelt werden muss:
$$h\hspace{0.03cm}'(t) \hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}}
\hspace{0.7cm}\{H_{\rm L}\hspace{-0.05cm}'(p)\cdot {\rm e}^{p t}\}=
\frac{\rm d}{{\rm d}p}\hspace{0.15cm}
\left \{ \frac{p +0.25}{(p
+0.5)^2} \cdot (p
+0.5)^2 \cdot {\rm e}^{p
\hspace{0.05cm}t}\right\}
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5}
= \hspace{0.2cm}\frac{\rm d}{{\rm d}p}\hspace{0.15cm}
\left \{ (p
+0.25) \cdot {\rm e}^{p
\hspace{0.05cm}t}\right\}
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5}
\hspace{0.05cm} .$$
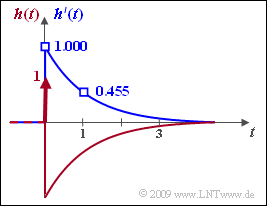
Mit der Produktregel der Differentialrechnung erhält man: $$h\hspace{0.03cm}'(t) \hspace{0.15cm} = \hspace{0.15cm} {\rm e}^{p \hspace{0.05cm}t} + ( p + 0.25) \cdot t \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} = \hspace{0.15cm} (1- {t}/{4}) \cdot{\rm e}^{-t/2} \hspace{0.05cm} $$ $$\Rightarrow \hspace{0.3cm}h\hspace{0.03cm}'(t = 0) \hspace{0.15cm} = \underline{1}\hspace{0.05cm} ,\hspace{0.3cm} h\hspace{0.03cm}'(t = 1) \hspace{0.15cm} = \underline {0.455}\hspace{0.05cm} \hspace{0.05cm} ,\hspace{0.3cm} h\hspace{0.03cm}'(t \rightarrow \infty) \hspace{0.15cm} = \underline {= 0}\hspace{0.05cm} .$$ Die Grafik zeigt als blaue Kurve $h'(t)$ und als rote Kurve die gesamte Impulsantwort $$h(t) = \delta (t) - (1- {t}/{4}) \cdot{\rm e}^{-t/2} \hspace{0.05cm}.$$