Aufgaben:Aufgabe 3.8: Rate Compatible Punctured Convolutional Codes: Unterschied zwischen den Versionen
| Zeile 16: | Zeile 16: | ||
Unter Letzterem versteht man, dass nach der herkömmlichen Faltungscodierung aus dem Codewort $\underline{x}^{(0)}$ entsprechend der Punktierungsmatrix $\mathbf{P}_l \ \rm Bits$ weggelassen werden und das verkürzte Codewort $\underline{x}^{(l)}$ übertragen wird. Kann das punktierte Codewort im Empfänger nicht korrekt decodiert werden, fordert der Empfänger vom Sender weitere Redundanz in Form der zuvor auspunktierten Bits an. Somit wird die Übertragung von nicht benötigter Redundanz verhindert und der Durchsatz an die Kanalgegebenheiten angepasst. | Unter Letzterem versteht man, dass nach der herkömmlichen Faltungscodierung aus dem Codewort $\underline{x}^{(0)}$ entsprechend der Punktierungsmatrix $\mathbf{P}_l \ \rm Bits$ weggelassen werden und das verkürzte Codewort $\underline{x}^{(l)}$ übertragen wird. Kann das punktierte Codewort im Empfänger nicht korrekt decodiert werden, fordert der Empfänger vom Sender weitere Redundanz in Form der zuvor auspunktierten Bits an. Somit wird die Übertragung von nicht benötigter Redundanz verhindert und der Durchsatz an die Kanalgegebenheiten angepasst. | ||
| + | |||
Version vom 16. Dezember 2017, 15:28 Uhr
Eine wichtige Anwendung für punktierte Faltungscodes sind die Rate Compatible Punctured Convolutional Codes (oder kurz RCPC–Codes), die 1988 von Joachim Hagenauer vorgeschlagen wurden Hag88. Ausgehend von einem Muttercode $C_0$ mit der Rate $R_0 = 1/n$ werden durch verschiedene Punktierungsmatrizen $\mathbf{P}_l$ andere Codes $C_l$ mit höherer Coderate $R_l > R_0$ festgelegt.
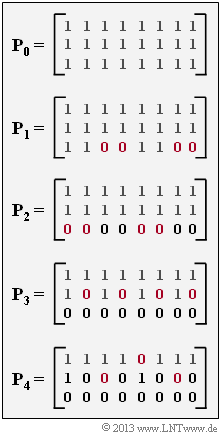
Rechts sind die zu analysierenden Punktierungsmatrizen $\mathbf{P}_0, \ ... \ , \ \mathbf{P}_4$ dargestellt. Ist bei der Matrix $\mathbf{P}_l$ das Matrixelement $P_{ij} = 1$, so wird das entsprechende Codebit übertragen, während $P_{ij} = 0$ auf eine Punktierung hinweist. Im Fragebogen verwenden wir für das Element $P_{ij}$ der Matrix $\mathbf{P}_l$ auch die kürzere Schreibweise $P_{ij}^{(l)}$.
In der obigen Darstellung sind alle die Nullen in der Matrix $\mathbf{P}_l$ rot markiert, die in der Matrix $\mathbf{P}_{l–1}$ noch Einsen waren. Durch diese Maßnahme wird die Coderate $R_{l–1}$ gegenüber $R_l$ vergrößert.
Die RCPC–Codes eignen sich gut zur Realisierung von
- ungleichem Fehlerschutz für hybride ARQ–Verfahren,
- Systemen mit inkrementeller Redundanz-
Unter Letzterem versteht man, dass nach der herkömmlichen Faltungscodierung aus dem Codewort $\underline{x}^{(0)}$ entsprechend der Punktierungsmatrix $\mathbf{P}_l \ \rm Bits$ weggelassen werden und das verkürzte Codewort $\underline{x}^{(l)}$ übertragen wird. Kann das punktierte Codewort im Empfänger nicht korrekt decodiert werden, fordert der Empfänger vom Sender weitere Redundanz in Form der zuvor auspunktierten Bits an. Somit wird die Übertragung von nicht benötigter Redundanz verhindert und der Durchsatz an die Kanalgegebenheiten angepasst.
Hinweise:
- Die Aufgabe bezieht sich auf die letzte Seite des Codebeschreibung mit Zustands– und Trellisdiagramm.
- Die RCPC–Codes wurden 1988 von Joachim Hagenauer erfunden, von 1993 bis 2006 Leiter des Lehrstuhls für Nachrichtentechnik (LNT) der Technischen Universität München. Die Verantwortlichen des von Ihnen gerade genutzten Lerntutorials – Günter Söder und Klaus Eichin – danken ihrem langjährigen Chef für die Unterstützung und Förderung unseres LNTwww–Projekts während der ersten Jahre.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(2) Für die Rate des Codes $C_l = p/N_l$, wobei $N_l$ die Anzahl aller Einsen in der Punktierungsmatrix $\mathbf{P}_l$ und $p$ die Punktierungsperiode bezeichnet:
- $R_0 = 8/24 = 1/3 = \underline{0.333}$,
- $R_1 = 8/20 = 2/5 = \underline{0.400}$,
- $R_2 = 8/16 = 1/2 = \underline{0.500}$,
- $R_3 = 8/12 = 2/3 = \underline{0.667}$,
- $R_4 = 8/9 = \underline{0.889}$.
(3) Alle Einsen in der Matrix $\mathbf{P}_4$ sind auch in den darüber liegenden Matrizen $\mathbf{P}_3, \ ... \ , \ \mathbf{P}_0$ enthalten. In der Matrix $\mathbf{P}_3$ kommen gegenüber $\mathbf{P}_4$ drei Einsen hinzu, in der Matrix $\mathbf{P}_2$ gegenüber $\mathbf{P}_3$ nochmals vier, usw. ⇒ Richtig sind die Lösungsvorschläge 1 und 4.