Aufgaben:Aufgabe 1.4: Maximum–Likelihood–Entscheidung: Unterschied zwischen den Versionen
Aus LNTwww
Wael (Diskussion | Beiträge) |
Wael (Diskussion | Beiträge) |
||
| Zeile 20: | Zeile 20: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Es sei $\underline{y} = (1, 0, 0, 0, 1)$. Welche Entscheidungen erfüllen das ML–Kriterium? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $\underline{z} = \underline{x}_{0} = (0, 0, 0, 0, 0)$, |
| − | + | + | - $\underline{z} = \underline{x}_{1} = (0, 1, 0, 1, 0)$, |
| + | + $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$, | ||
| + | - $\underline{z} = \underline{x}_{3} = (1, 1, 1, 1, 1)$. | ||
| − | { | + | {Es sei $\underline{y} = (0, 0, 0, 1, 0)$. Welche Entscheidungen erfüllen das ML–Kriterium? |
| + | |type="[]"} | ||
| + | + $\underline{z} = \underline{x}_{0} = (0, 0, 0, 0, 0)$, | ||
| + | + $\underline{z} = \underline{x}_{1} = (0, 1, 0, 1, 0)$, | ||
| + | - $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$, | ||
| + | - $\underline{z} = \underline{x}_{3} = (1, 1, 1, 1, 1)$. | ||
| + | |||
| + | {Welche Entscheidung trifft der ML–Decoder für $\underline{y} = (1, 0, 1, 1, 1)$, wenn ihm mitgeteilt wird, dass die beiden letzten Symbole eher unsicher sind? | ||
| + | |type="[]"} | ||
| + | - $\underline{z} = \underline{x}_{0} = (0, 0, 0, 0, 0)$, | ||
| + | - $\underline{z} = \underline{x}_{1} = (0, 1, 0, 1, 0)$, | ||
| + | + $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$, | ||
| + | - $\underline{z} = \underline{x}_{3} = (1, 1, 1, 1, 1)$. | ||
| + | |||
| + | |||
| + | |||
| + | {Zu welchem Informationswort $\upsilon = (\upsilon_{1}, \upsilon_{2})$ führt diese Entscheidung? | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\upsilon_{1}$ = { 1 3% } |
| + | $\upsilon_{2}$ = { 0 3% } | ||
Version vom 28. November 2017, 17:47 Uhr
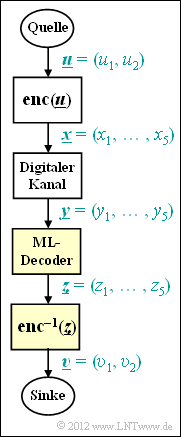
Wir betrachten das digitale Übertragungssystem entsprechend der Grafik. Berücksichtigt sind dabei:
- ein systematischer (5, 2)–Blockcode C mit den Codeworten
- $$\underline{x}_{0} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 0, 0, 0, 0) \hspace{0.05cm},$$ $$\underline{x}_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 1, 0, 1, 0) \hspace{0.05cm},$$ $$\underline{x}_{2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 0, 1, 0, 1) \hspace{0.05cm},$$ $$\underline{x}_{3} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 1, 1, 1, 1) \hspace{0.05cm},$$
- ein digitales (binäres) Kanalmodell, das den Vektor x ∈ GF($2^{5}$) in den Vektor $\underline{y} \in {\rm GF} (2^{5}$) verfälscht,
- ein Maximum–Likelihood–Decoder mit der Entscheidungsregel
- $$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i}).$$
In der Gleichung bezeichnet $d_{\rm H} (\underline{y},\underline{x_{i}})$ die Hamming–Distanz zwischen Empfangswort $\underline{y}$ und dem (möglicherweise) gesendeten Codewort $\underline{x_{i}}$.
Hinweis:
Die Aufgabe gehört zum Kanalmodelle und Entscheiderstrukturen
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.