Aufgaben:Aufgabe 2.5: Ternäre Signalübertragung

• Zurück zum Buch

WDF eines verrauschten Ternärsignals

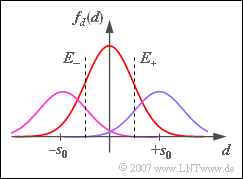
Betrachtet wird ein ternäres Übertragungssystem ($M = 3$) mit den möglichen Amplitudenwerten $–s_0$, $0$ und $+s_0$. Bei der Übertragung addiert sich dem Signal ein additives Gaußsches Rauschen mit dem Effektivwert $\sigma_d$. Die Rückgewinnung des dreistufigen Digitalsignals beim Empfängers geschieht mit Hilfe von zwei Entscheiderschwellen bei $E_{–}$ bzw. $E_{+}$.

Zunächst werden die Auftrittswahrscheinlichkeiten von den drei Eingangssymbolen als gleichwahrscheinlich angenommen

$$p_{\rm -} = {\rm Pr}(-s_0) = {1}/{ 3}, \hspace{0.15cm} p_{\rm 0} = {\rm Pr}(0) = {1}/{ 3}, \hspace{0.15cm} p_{\rm +} = {\rm Pr}(+s_0) ={1}/{ 3}\hspace{0.05cm}.$$

Die Entscheiderschwellen liegen vorerst mittig bei $E_{–} = \, –s_0/2$ und $E_{+} = +s_0/2$.

Ab der Teilaufgabe (3) gelten für die Symbolwahrscheinlichkeiten $p_{–} = p_+ = 1/4$ und $p_0 = 1/2$, wie in der Grafik dargestellt. Für diese Konstellation soll durch Variation der Entscheiderschwellen $E_{–}$ und $E_+$ die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ minimiert werden.

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel Redundanzfreie Codierung.
• Für die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ eines $M$–stufigen Nachrichtenübertragungssystems mit gleichwahrscheinlichen Eingangssymbolen und Schwellenwerten genau in der Mitte zwischen zwei benachbarten Amplitudenstufen gilt:

$$p_{\rm S} = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( {\frac{s_0}{(M-1) \cdot \sigma_d}}\right) \hspace{0.05cm}.$$

• Die Fehlerwahrscheinlichkeitswerte gemäß der ${\rm Q}$– bzw. der ${\rm erfc}$–Funktion können Sie mit folgendem Interaktionsmodul numerisch ermitteln: Komplementäre Gaußsche Fehlerfunktionen
• Verwenden Sie zur Überprüfung der Ergebnisse das Berechnungsmodul Symbolfehlerwahrscheinlichkeit von Digitalsystemen
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche Symbolfehlerwahrscheinlichkeit ergibt sich mit dem (normierten) Rauscheffektivwert $\sigma_d/s_0 = 0.25$ bei gleichwahrscheinlichen Symbolen?

$p_0 = 1/3, \sigma_d = 0.25 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ $\ \%$

2

Wie ändert sich die Symbolfehlerwahrscheinlichkeit mit $\sigma_d/s_0 = 0.5$?

$p_0 = 1/3, \sigma_d = 0.5 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ $\ \%$

3

Welcher Wert ergibt sich mit $p_{–} = p_+ = 0.25$ und $p_0 = 0.5$?

$p_0 = 1/2, \sigma_d = 0.5 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ $\ \%$

4

Bestimmen Sie die optimalen Schwellen $E_+$ und $E_{–} = \, –E_+$ für $p_0 = 1/2$.

$p_0 = 1/2, \sigma_d = 0.5 \text{:} \hspace{0.4cm} E_{\rm +, \ opt} \ = \ $

5

Welche Fehlerwahrscheinlichkeit ergibt sich bei optimalen Schwellen?

${\rm optimale \ Schwellen} \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ $\ \%$

6

Wie lauten die optimalen Schwellenwerte für $p_0 = 0.2$ und $p_{–} = p_+ = 0.4$?

$p_0 = 0.2, \sigma_d = 0.5 \text{:} \hspace{0.4cm} E_{\rm +, \ opt} \ = \ $

7

Welche Symbolfehlerwahrscheinlichkeit ergibt sich nun? Interpretation.

${\rm optimale \ Schwellen} \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ $\ \%$

Musterlösung

Musterlösung

(1)  Entsprechend der angegebenen Gleichung gilt mit $M = 3$ und $\sigma_d/s_0 = 0.25$:

$$p_{\rm S} = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( {\frac{s_0}{(M-1) \cdot \sigma_d}}\right)= {4}/{ 3}\cdot {\rm Q}(2) ={4}/{ 3}\cdot 0.0228\hspace{0.15cm}\underline {\approx 3 \,\%} \hspace{0.05cm}.$$

(2)  Bei doppeltem Rauscheffektivwert nimmt auch die Fehlerwahrscheinlichkeit signifikant zu:

$$p_{\rm S} = {4}/{ 3}\cdot {\rm Q}(1)= {4}/{ 3}\cdot 0.1587 \hspace{0.15cm}\underline {\approx 21.2 \,\%} \hspace{0.05cm}.$$

(3)  Die beiden äußeren Symbole werden jeweils mit der Wahrscheinlichkeit $p = {\rm Q}(s_0/(2 \cdot \sigma_d)) = 0.1587$ verfälscht. Die Verfälschungswahrscheinlichkeit des Symbols „$0$” ist doppelt so groß (es wird durch zwei Schwellen begrenzt). Unter Berücksichtigung der einzelnen Symbolwahrscheinlichkeiten erhält man:

$$p_{\rm S} = {1}/{ 4}\cdot p + {1}/{ 2}\cdot 2p +{1}/{ 4}\cdot p = 1.5 \cdot p = 1.5 \cdot 0.1587 \hspace{0.15cm}\underline {\approx 23.8 \,\%} \hspace{0.05cm}.$$

(4)  Da das Symbol „$0$” häufiger auftritt und zudem in beiden Richtungen verfälscht werden kann, sollten die Schwellen nach außen verschoben werden. Die optimale Entscheiderschwelle $E_{\rm +, \ opt}$ ergibt sich aus dem Schnittpunkt der beiden in der Grafik gezeigten Gaußfunktionen. Es muss gelten:

$$:$$\frac{ 1/2}{ \sqrt{2\pi} \cdot \sigma_d} \cdot {\rm exp} \left[ - \frac{ E_{\rm +}^2}{2 \cdot \sigma_d^2}\right]

  = \frac{ 1/4}{ \sqrt{2\pi} \cdot \sigma_d} \cdot  {\rm exp} \left[ - \frac{ (s_0 -E_{\rm +})^2}{2 \cdot \sigma_d^2}\right]$$

[[Datei:P_ID1328__Dig_A_2_5e.png|right|frame|Optimale Schwellen bei einem Ternärsystem]]

:$$\Rightarrow \hspace{0.3cm}   {\rm exp} \left[  \frac{ (s_0 -E_{\rm +})^2 - E_{\rm +}^2}{2 \cdot
 \sigma_d^2}\right]= {1}/{ 2}$$
:$$\Rightarrow \hspace{0.3cm}   {\rm exp} \left[  \frac{ 1 -2 \cdot E_{\rm +}/s_0}{2 \cdot
 \sigma_d^2/s_0^2}\right]= {1}/{ 2}$$
:$$\Rightarrow \hspace{0.3cm}\frac{ E_{\rm +}}{s_0}= \frac{1}

{ 2}+ \frac{\sigma_d^2} {s_0^2} \cdot {\rm ln}(2)\hspace{0.15cm}\underline {=0.673}\hspace{0.15cm}\approx {2}/ {3} \hspace{0.05cm}.$$ '''(5)'''  Mit dem näherungsweisen Ergebnis aus (4) erhält man: :$$p_{\rm S} \ = \

{ 1}/{4} \cdot {\rm Q} \left( {\frac{s_0/3}{
\sigma_d}}\right)+ 2 \cdot { 1}/{2} \cdot {\rm Q} \left( {\frac{2s_0/3}{
\sigma_d}}\right) +{ 1}/{4} \cdot {\rm Q} \left( {\frac{s_0/3}{
\sigma_d}}\right) = $$
:$$\ = \ { 1}/{2}  \cdot {\rm Q} \left( 2/3 \right)+ {\rm Q} \left( 4/3
\right)=
{ 1}/{2} \cdot 0.251 + 0.092 \hspace{0.15cm}\underline {\approx 21.7 \,\%}
\hspace{0.05cm}.$$


'''(6)'''  [[Datei:P_ID1329__Dig_A_2_5g.png|right|frame|Optimale Schwellen bei einem Ternärsystem]] Nach ähnlicher Rechnung wie unter Punkt (4) erhält man $E_+ = 1 \, –0.0673 \ \underline{= 0.327} \approx 1/3$. Es gilt weiterhin $E_{–} = \, –E_+$.


'''(7)'''  Ähnlich wie in der Musterlösung zur Teilaufgabe (5) erhält man nun:
:$$p_{\rm S} \ = \ 0.4 \cdot {\rm Q} \left( 4/3 \right)+ 2 \cdot 0.2 \cdot{\rm Q} \left( 2/3
\right)+0.4 \cdot {\rm Q} \left( 4/3 \right) =$$
:$$\ = \

0.4 \cdot (0.092 + 0.251 + 0.092)

 \hspace{0.15cm}\underline {\approx 17.4 \,\%}
\hspace{0.05cm}.$$

Es ergibt sich demnach eine kleinere Symbolfehlerwahrscheinlichkeit ($17.4 \ \%$ gegenüber $21.2 \ \%$) als bei gleichwahrscheinlichen Amplitudenkoeffizienten. Allerdings liegt nun keine redundanzfreie Codierung mehr vor, auch wenn die Amplitudenkoefiizienten statistisch voneinander unabhängig sind. Während bei gleichwahrscheinlichen Ternärsymbolen die Entropie $H = {\rm log}_2(3) = 1.585 {\rm bit/Ternärsymbol}$ beträgt, woraus die äquivalente Bitrate (der Informationsfluss) $R_{\rm B} = H/T$ berechnet werden kann, gilt mit den Wahrscheinlichkeiten $p_0 = 0.2$ und $p_{–} = p_+ = 0.4$:
:$$H  \ = \ 0.2 \cdot {\rm log_2} (5) + 2 \cdot 0.4 \cdot {\rm log_2} (2.5)= $$
:$$\ = \ 0.2 \cdot 2.322 + 0.8 \cdot 1.322 \hspace{0.15cm}\underline {\approx 1.522\,\, {\rm

bit/Tern\ddot{a}rsymbol}}

\hspace{0.05cm}.$$

Die äquivalente Bitrate ist also um $4 \ \%$ kleiner, als sie für $M = 3$ maximal möglich wäre.