Aufgaben:Aufgabe 2.6Z: 4B3T-Code nach Jessop und Waters: Unterschied zwischen den Versionen
| Zeile 11: | Zeile 11: | ||
*In der Tabelle stehen „+” und „–” für die Amplitudenkoeffizienten $a_{\nu} = +1$ bzw. $a_{\nu} = –1$. | *In der Tabelle stehen „+” und „–” für die Amplitudenkoeffizienten $a_{\nu} = +1$ bzw. $a_{\nu} = –1$. | ||
*Die Laufvariable $l$ kennzeichnet die einzelnen Blöcke. | *Die Laufvariable $l$ kennzeichnet die einzelnen Blöcke. | ||
| − | *In der Aufgabe wird von den folgenden sechs Eingangsblöcken ausgegangen: $\rm LLHL\hspace{0.1cm} HLLH \hspace{0.1cm}LHHH \hspace{0.1cm}HLLH \hspace{0.1cm}HLHH \hspace{0.1cm}HHLH$ | + | *In der Aufgabe wird von den folgenden sechs Eingangsblöcken ausgegangen: |
| + | :$$\rm LLHL\hspace{0.1cm} HLLH \hspace{0.1cm}LHHH \hspace{0.1cm}HLLH \hspace{0.1cm}HLHH \hspace{0.1cm}HHLH.$$ | ||
*Die laufende digitale Summe ist mit $\Sigma_{0} = 0$ (Teilaufgaben bis einschließlich (2) bzw. $\Sigma_{0} = 5$ (Teilaufgabe (5) initialisiert. | *Die laufende digitale Summe ist mit $\Sigma_{0} = 0$ (Teilaufgaben bis einschließlich (2) bzw. $\Sigma_{0} = 5$ (Teilaufgabe (5) initialisiert. | ||
| Zeile 22: | Zeile 23: | ||
*Damit eine solche Verwirrung vermieden wird und die „0” nicht in beiden Alphabeten (binär und ternär) – dazu noch mit unterschiedlicher Bedeutung – auftritt, haben wir die zugegebenerweise etwas gewöhnungsbedürftige Nomenklatur verwendet. Wir sind uns durchaus bewusst, dass auch unsere Nomenklatur manche Leser verwirren wird. | *Damit eine solche Verwirrung vermieden wird und die „0” nicht in beiden Alphabeten (binär und ternär) – dazu noch mit unterschiedlicher Bedeutung – auftritt, haben wir die zugegebenerweise etwas gewöhnungsbedürftige Nomenklatur verwendet. Wir sind uns durchaus bewusst, dass auch unsere Nomenklatur manche Leser verwirren wird. | ||
*Sie können die Ergebnisse mit dem Interaktionsmodul [[Prinzip der 4B3T–Codierung]] überprüfen. | *Sie können die Ergebnisse mit dem Interaktionsmodul [[Prinzip der 4B3T–Codierung]] überprüfen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Zeile 39: | Zeile 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Codieren Sie die Eingangsfolge | + | {Codieren Sie die Eingangsfolge $\rm LLHL\hspace{0.1cm} HLLH \hspace{0.1cm}LHHH \hspace{0.1cm}HLLH \hspace{0.1cm}HLHH \hspace{0.1cm}HHLH$ ausgehend vom Initialwert ${\it \Sigma}_{0} = 0$. <br>Wie lautet die ternäre Ausgangsfolge? |
|type="[]"} | |type="[]"} | ||
| − | - $ 0 – + | + | - $ \text{0 – +} \hspace{0.4cm} \text{– + +} \hspace{0.4cm} \text {– – –} \hspace{0.5cm} \text{– ++} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 +}, $ |
| − | + $ 0 – + \ \ | + | + $ \text{0 – +} \hspace{0.4cm} \text{– + +} \hspace{0.4cm} \text{+ + +} \hspace{0.4cm} \text{+ – –} \hspace{0.4cm} \text{– 0 0} \hspace{0.4cm} \text{0 0 +}, $ |
| − | - | + | - $ \text{0 – +} \hspace{0.4cm} \text{+ – –} \hspace{0.4cm} \text{– – –} \hspace{0.5cm} \text{– + +} \hspace{0.4cm} \text{+ 0 0} \hspace{0.4cm} \text{0 0 –}. $ |
| − | {Welchen Wert hat die laufende digitale Summe nach Codierung der | + | {Welchen Wert hat die laufende digitale Summe nach Codierung der sechs Blöcke? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | ${\it \Sigma}_{6} \ = \ $ { 3 3% } |
{Wieviele Ternärwerte „$+1$” können maximal aufeinanderfolgen? | {Wieviele Ternärwerte „$+1$” können maximal aufeinanderfolgen? | ||
| Zeile 57: | Zeile 49: | ||
$k_{0} \ = \ $ { 4 3% } | $k_{0} \ = \ $ { 4 3% } | ||
| − | {Welchen Wert hat die laufende digitale Summe nach Codierung der | + | {Welchen Wert hat die laufende digitale Summe nach Codierung der sechs Blöcke, wenn von ${\it \Sigma}_{0} = 5$ ausgegangen wird? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | ${\it \Sigma}_{6} \ = \ $ { 2 3% } |
Version vom 17. November 2017, 14:14 Uhr
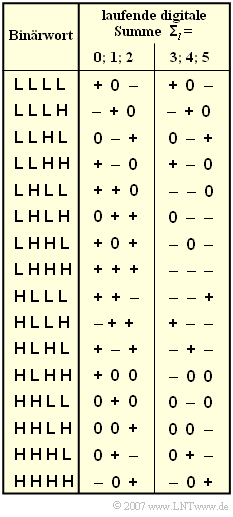
Die Grafik zeigt die zwei Codetabellen für den 4B3T–Code nach Jessop und Waters. Je nach dem aktuellen Wert der laufenden digitalen Summe
- $${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.05cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu \hspace{0.05cm}$$
gibt es für jedes binäre Eingangstupel $\rm LLLL$ ... $\rm \ HHHH$ zwei unterschiedliche ternäre Codefolgen.
- In der Tabelle stehen „+” und „–” für die Amplitudenkoeffizienten $a_{\nu} = +1$ bzw. $a_{\nu} = –1$.
- Die Laufvariable $l$ kennzeichnet die einzelnen Blöcke.
- In der Aufgabe wird von den folgenden sechs Eingangsblöcken ausgegangen:
- $$\rm LLHL\hspace{0.1cm} HLLH \hspace{0.1cm}LHHH \hspace{0.1cm}HLLH \hspace{0.1cm}HLHH \hspace{0.1cm}HHLH.$$
- Die laufende digitale Summe ist mit $\Sigma_{0} = 0$ (Teilaufgaben bis einschließlich (2) bzw. $\Sigma_{0} = 5$ (Teilaufgabe (5) initialisiert.
Hinweise:
- Die Aufgabe gehört zum Kapitel Blockweise Codierung mit 4B3T-Codes.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Die Binärsymbole werden in diesem Lerntutorial mit L („Low”) und H („High”) bezeichnet. Häufig findet man in der Literatur auch die Binärsymbole L und 0 (statt H). Manchmal entspricht aber auch L unserem H und 0 dem L.
- Damit eine solche Verwirrung vermieden wird und die „0” nicht in beiden Alphabeten (binär und ternär) – dazu noch mit unterschiedlicher Bedeutung – auftritt, haben wir die zugegebenerweise etwas gewöhnungsbedürftige Nomenklatur verwendet. Wir sind uns durchaus bewusst, dass auch unsere Nomenklatur manche Leser verwirren wird.
- Sie können die Ergebnisse mit dem Interaktionsmodul Prinzip der 4B3T–Codierung überprüfen.
Fragebogen
Musterlösung
2 Ausgehend von $\Sigma_{0} = 0$ ergeben sich für die laufende digitale Summe folgende Werte:
- $\Sigma_{1} = 0,$
- $\Sigma_{2} = 1,$
- $\Sigma_{3} = 4,$
- $\Sigma_{4} = 3,$
- $\Sigma_{5} = 2,$
- $\Sigma_{6} \ \underline{= 3}.$
3 Es gilt $K_{+1}\underline{ = 6}$. Auch in der codierten Folge dieser Aufgabe erkennt man sechs aufeinanderfolgende Pluszeichen, die von insgesamt drei Blöcken stammen: Zwei am Ende des zweiten Blockes, dann drei „$+1$” im Block $3$ und schließlich eine „$+1$” am Beginn des vierten Blocks. In gleicher Weise gilt $K_{-1} = 6$ (siehe Lösungsvorschlag 3 in der ersten Teilaufgabe).
4 Ist $\Sigma_{l} = 2$, so führt die Binärfolge „HLHH HHLH” zur Ternärfolge „$+ 0 0 0 0 –$”. Mehr als $K_{0}\underline{ = 4}$ aufeinanderfolgende Nullen sind nicht möglich.
5 Die Ternärfolge lautet hier: $0 – + \ \ \ + – – \ \ \ – – – \ \ \ – + + \ \ \ + 0 0 \ \ \ 0 0 –$. Die laufende digitale Summe baut sich wie folgt auf:
- $\Sigma_{1} = 5,$
- $\Sigma_{2} = 4,$
- $\Sigma_{3} = 1,$
- $\Sigma_{4} = 2,$
- $\Sigma_{5} = 3,$
- $\Sigma_{6} \ \underline{= 2}.$