Aufgaben:Aufgabe 1.4Z: Komplexes Nyquistspektrum: Unterschied zwischen den Versionen
| Zeile 40: | Zeile 40: | ||
<quiz display=simple> | <quiz display=simple> | ||
| + | |||
| + | {Für die ersten Teilfragen gelte $B = 0$. Wie groß ist die Nyquistfrequenz? | ||
| + | |type="{}"} | ||
| + | $f_{\rm Nyq} \ = \ $ { 5 3% } $\ \rm kHz$ | ||
| + | |||
| + | {Welcher Rolloff–Faktor liegt hier vor? | ||
| + | |type="{}"} | ||
| + | $r \ = \ $ { 0.4 3% } | ||
| + | |||
| + | {Berechnen Sie den Maximalwert $g_{0}$ des Nyquistimpulses $g(t)$. | ||
| + | |type="{}"} | ||
| + | $g_{0} \ = \ ${ 1 3% } $\ \rm V$ | ||
| + | |||
| + | {Berechnen Sie $g(t)$ für die Zeitpunkte $t = 100\ \mu \rm s$ und $t = 200\ \mu \rm s$. | ||
| + | |type="{}"} | ||
| + | $B = 0: g(t = 100\ \mu \rm s) \ = \ $ { 0 3% } $\ \rm V$ | ||
| + | $B = 0: g(t = 200\ \mu \rm s) \ = \ $ { 0 3% } $\ \rm V$ | ||
| + | |||
| + | {Berechnen Sie den Impulswert zur Zeit $t = 250\ \mu \rm s$. | ||
| + | |type="{}"} | ||
| + | $B = 0: g(t = 250\ \mu \rm s) \ = \ $ { 0 3% } $\ \rm V$ | ||
| + | |||
{Multiple-Choice Frage | {Multiple-Choice Frage | ||
|type="[]"} | |type="[]"} | ||
| Zeile 48: | Zeile 70: | ||
{Input-Box Frage | {Input-Box Frage | ||
|type="{}"} | |type="{}"} | ||
| − | $\alpha$ | + | $\alpha \ = \ $ { 0.3 } |
Version vom 5. November 2017, 11:45 Uhr
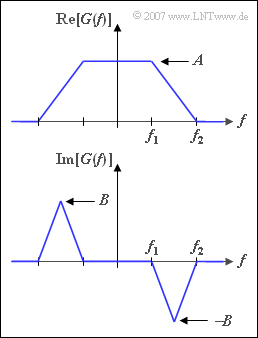
Betrachtet wird ein Impuls $g(t)$ mit dem Spektrum gemäß der Skizze. Man erkennt aus dieser Darstellung:
- Der Realteil von $G(f)$ verläuft trapezförmig mit den beiden Eckfrequenzen $f_{1} = 3 \ \rm kHz$ und $f_{2} = 7 \ \rm kHz$.
Im Bereich $|f| < f_{1}$ gilt $Re[G(f)]$ = $A = 10^{-4} \ \rm V/Hz$.
- Der Imaginärteil von $G(f)$ wird für die Teilaufgaben (1) bis (5) stets zu $0$ angenommen. In diesem Fall ist $g(t)$ sicher ein Nyquistimpuls.
- Ab der Teilaufgabe (6) hat der Imaginärteil $Im[G(f)]$ im Bereich $f_{1} \leq | f | \leq f_{2}$ einen Dreiecksverlauf mit den Werten $\pm B$ bei den Dreieckspitzen.
Zu überprüfen ist, ob der Impuls $g(t)$ auch mit komplexem Spektrum der ersten Nyquistbedingung genügt:
- $$g(\nu T) = \left\{ \begin{array}{c} g_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} \nu = 0 \hspace{0.05cm}, \\ \nu \ne 0 \hspace{0.1cm}. \\ \end{array}$$
Im Verlauf dieser Aufgabe wird auf folgende Beschreibungsgrößen Bezug genommen:
- Die Nyquistfrequenz gibt den Symmetriepunkt des Flankenabfalls an:
- $$f_{\rm Nyq}= \frac{1}{2T}= \frac{f_1 +f_2 } {2 }\hspace{0.05cm}.$$
- Der Rolloff–Faktor ist ein Maß für die Flankensteilheit:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.05cm}.$$
Hinweis:
Die Aufgabe bezieht sich auf das Eigenschaften von Nyquistsystemen Als bekannt vorausgesetzt werden kann die Fourierrücktransformierte $g(t)$ eines trapezförmigen Nyquistspektrums mit Rolloff–Faktor $r$:
Ein dreieckförmiges Tiefpass–Spektrum $G(f)$, das auf $| f | < f_{0}$ begrenzt ist und für das $G(f = 0) = B$ gilt, führt nach der Fourierrücktransformation zu folgender Zeitfunktion:
- $$g ( t )= B \cdot f_0 \cdot {\rm si}^2 \left ( {\pi f_0 t}\right)\hspace{0.05cm}.$$
Fragebogen
Musterlösung