Signaldarstellung/Fouriertransformation und -rücktransformation: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
David (Diskussion | Beiträge) |
||
| Zeile 100: | Zeile 100: | ||
*Anstatt die Fourierkoeffizienten $D_v'$ zu berechnen, wird nun stattdessen eine spektrale Dichte $X(f)$ ermittelt. Bei der Frequenz $f=v \cdot f_0'$ gilt dann: | *Anstatt die Fourierkoeffizienten $D_v'$ zu berechnen, wird nun stattdessen eine spektrale Dichte $X(f)$ ermittelt. Bei der Frequenz $f=v \cdot f_0'$ gilt dann: | ||
| − | $X(f = {\rm \nu} {f_{\rm 0}}') = \lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm} 0} ({{D_{\rm \nu}}'}/{{f_{\rm 0}}'}) = \lim_{{T_{\rm 0}}' \to \infty} ({D_{\rm \nu}}' \cdot {T_{\rm 0}}')$ . | + | $$X(f = {\rm \nu} {f_{\rm 0}}') = \lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm} 0} ({{D_{\rm \nu}}'}/{{f_{\rm 0}}'}) = \lim_{{T_{\rm 0}}' \to \infty} ({D_{\rm \nu}}' \cdot {T_{\rm 0}}')$$ . |
*Die Spektralfunktion (Dichte) $X(f)$ des aperiodischen Signals $x(t)$ ist im Spektrum $X_P(f)$ des vergleichbaren periodischen Signals $x_P(t)$ als Einhüllende erkennbar (siehe Grafiken). | *Die Spektralfunktion (Dichte) $X(f)$ des aperiodischen Signals $x(t)$ ist im Spektrum $X_P(f)$ des vergleichbaren periodischen Signals $x_P(t)$ als Einhüllende erkennbar (siehe Grafiken). | ||
*In der unteren Grafik entspricht $D_v'$ der rot hinterlegten Fläche des Frequenzintervalls um $v \cdot f_0'$ mit der Breite $f_0'$. | *In der unteren Grafik entspricht $D_v'$ der rot hinterlegten Fläche des Frequenzintervalls um $v \cdot f_0'$ mit der Breite $f_0'$. | ||
| + | [[Datei:P_ID397__Sig_T_3_1_S3_b_rah.png|250px|right|Vom periodischen zum aperiodischen Signal]] | ||
Verwendet man die auf der letzten Seite angegebenen Gleichungen, so erhält man: | Verwendet man die auf der letzten Seite angegebenen Gleichungen, so erhält man: | ||
| − | $X(f = {\rm \nu} \cdot {f_{\rm 0}}') = \lim_{{T_{\rm 0}'} \to \infty} \int ^{{T_{\rm 0}}'/2} _{-{T_{\rm 0}}'/2} x_{\rm P}(t) \, \cdot \, { \rm e}^{-\rm j 2\pi\nu \it {f_{\rm 0}}' t} \,{\rm d}t.$ | + | $$X(f = {\rm \nu} \cdot {f_{\rm 0}}') = \lim_{{T_{\rm 0}'} \to \infty} \int ^{{T_{\rm 0}}'/2} _{-{T_{\rm 0}}'/2} x_{\rm P}(t) \, \cdot \, { \rm e}^{-\rm j 2\pi\nu \it {f_{\rm 0}}' t} \,{\rm d}t.$$ |
Durch den gemeinsamen Grenzübergang ($T_0' \to \infty, f_0' \to 0$) wird nun | Durch den gemeinsamen Grenzübergang ($T_0' \to \infty, f_0' \to 0$) wird nun | ||
*aus dem periodischen Signal $x_P(t)$ das aperiodische Signal $x(t)$, und | *aus dem periodischen Signal $x_P(t)$ das aperiodische Signal $x(t)$, und | ||
| − | *aus der diskreten Frequenz $v \cdot | + | *aus der diskreten Frequenz $v \cdot f_0'$ die kontinuierliche Frequenzvariable $f$. |
| + | |||
Damit erhält man eine fundamentale Definition, welche die Berechnung der Spektralfunktion einer aperiodischen Zeitfunktion ermöglicht. Der Name dieser Spektraltransformation geht auf den französischen Physiker Jean-Baptiste-Joseph Fourier zurück. | Damit erhält man eine fundamentale Definition, welche die Berechnung der Spektralfunktion einer aperiodischen Zeitfunktion ermöglicht. Der Name dieser Spektraltransformation geht auf den französischen Physiker Jean-Baptiste-Joseph Fourier zurück. | ||
| Zeile 119: | Zeile 121: | ||
Die Spektralfunktion (oder kurz: das Spektrum) eines aperiodischen und gleichzeitig energiebegrenzten Signals $x(t)$ ist wie folgt zu berechnen: | Die Spektralfunktion (oder kurz: das Spektrum) eines aperiodischen und gleichzeitig energiebegrenzten Signals $x(t)$ ist wie folgt zu berechnen: | ||
| − | $X(f)= \hspace{0.05cm}\int \limits_{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t$ | + | $$X(f)= \hspace{0.05cm}\int \limits_{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t$$ |
| + | |||
| + | ⇒ Erstes Fourierintegral. | ||
| − | |||
{{end}} | {{end}} | ||
| Zeile 133: | Zeile 136: | ||
{{Beispiel}} | {{Beispiel}} | ||
Gegeben ist der skizzierte Zeitverlauf $x(t)$. Gesucht ist das zugehörige Spektrum $X(f)$. | Gegeben ist der skizzierte Zeitverlauf $x(t)$. Gesucht ist das zugehörige Spektrum $X(f)$. | ||
| + | |||
| + | [[Datei:P_ID330__Sig_T_3_1_S5_neu.png|250px|right|Rechteckimpuls]] | ||
Wir wenden dazu das erste Fourierintegral an. Aus obiger Darstellung ist zu erkennen, dass das Signal $x(t)$ für $|t| > T/2$ gleich 0 ist. Das bedeutet, dass das Integrationsintervall auf den Bereich $\pm T/2$ begrenzt werden kann. Damit erhält man den Ansatz: | Wir wenden dazu das erste Fourierintegral an. Aus obiger Darstellung ist zu erkennen, dass das Signal $x(t)$ für $|t| > T/2$ gleich 0 ist. Das bedeutet, dass das Integrationsintervall auf den Bereich $\pm T/2$ begrenzt werden kann. Damit erhält man den Ansatz: | ||
| − | $X(f) & = | + | $$ \begin{align} X(f) & = A \int_{-T/2}^{+T/2} {\rm e}^{-{\rm j2\pi} ft}\,{\rm d}t = \frac{ A}{-\rm j2\pi f}\left[ {\rm e}^{-{\rm j}2\pi ft}\right]_{-T/2}^{+T/2} \\ & = \frac{\it A}{-\rm j 2\pi f}\left[\cos({\rm \pi} f T)-{\rm j} \cdot \sin({\rm \pi} fT)-\cos({\rm \pi} fT)-{\rm j} \cdot \sin({\rm \pi} fT)\right]. \end{align} $$ |
| − | $\Rightarrow X(f)=A\cdot \frac{\sin({\rm \pi} fT)}{{\rm \pi} f}.$ | + | $$\Rightarrow X(f)=A\cdot \frac{\sin({\rm \pi} fT)}{{\rm \pi} f}.$$ |
Erweitert man Zähler und Nenner mit $T$, so erhält man: | Erweitert man Zähler und Nenner mit $T$, so erhält man: | ||
| − | $X(f)=A\cdot T \cdot\frac{\sin(\pi fT)}{\pi fT} = A\cdot T \cdot{\rm si }(\pi fT) .$ | + | $$X(f)=A\cdot T \cdot\frac{\sin(\pi fT)}{\pi fT} = A\cdot T \cdot{\rm si }(\pi fT) .$$ |
Die Funktion si($x$) = sin($x$)/$x$ wird auf der Seite Rechteckimpuls im Kapitel 3.2 noch eingehend analysiert. Man nennt sie ''si–Funktion'' oder auch ''Spaltfunktion''. | Die Funktion si($x$) = sin($x$)/$x$ wird auf der Seite Rechteckimpuls im Kapitel 3.2 noch eingehend analysiert. Man nennt sie ''si–Funktion'' oder auch ''Spaltfunktion''. | ||
| Zeile 160: | Zeile 165: | ||
Das Spektrum $X(f)$ eines Signals $x(t)$ lautet gemäß dem „Ersten Fourierintegral”: | Das Spektrum $X(f)$ eines Signals $x(t)$ lautet gemäß dem „Ersten Fourierintegral”: | ||
| − | $X(f)= \hspace{0.05cm}\int _{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$ | + | $$X(f)= \hspace{0.05cm}\int _{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$ |
Wie auf der letzten Seite an einem einfachen Beispiel gezeigt wurde, ist dieses Integral bei einem energiebegrenzten Signal $x(t)$ problemlos lösbar. | Wie auf der letzten Seite an einem einfachen Beispiel gezeigt wurde, ist dieses Integral bei einem energiebegrenzten Signal $x(t)$ problemlos lösbar. | ||
| Zeile 170: | Zeile 175: | ||
divergiert aber das Fourierintegral. Unter Einbeziehung einer beidseitig abfallenden Hilfsfunkion $\epsilon (t)$ kann allerdings die Konvergenz erzwungen werden: | divergiert aber das Fourierintegral. Unter Einbeziehung einer beidseitig abfallenden Hilfsfunkion $\epsilon (t)$ kann allerdings die Konvergenz erzwungen werden: | ||
| − | $X(f) = \lim_{\varepsilon \to 0} \int _{-\infty} ^{{+}\infty} x(t) \cdot {\rm e}^{\it -\varepsilon | \hspace{0.01cm} t \hspace{0.01cm} |} \cdot {\rm e}^{{-\rm j 2 \pi}\it ft} \,{\rm d}t.$ | + | $$X(f) = \lim_{\varepsilon \to 0} \int _{-\infty} ^{{+}\infty} x(t) \cdot {\rm e}^{\it -\varepsilon | \hspace{0.01cm} t \hspace{0.01cm} |} \cdot {\rm e}^{{-\rm j 2 \pi}\it ft} \,{\rm d}t.$$ |
Solche nicht energiebegrenzten Signale führen im Spektrum zu Diracfunktionen, manchmal auch „Distributionen” genannt. Man bezeichnet diesen allgemeinen Funktionalzusammenhang $X(f) = F[x(t)]$ als '''Fouriertransformation''' und verwendet hierfür die Kurzschreibweise: | Solche nicht energiebegrenzten Signale führen im Spektrum zu Diracfunktionen, manchmal auch „Distributionen” genannt. Man bezeichnet diesen allgemeinen Funktionalzusammenhang $X(f) = F[x(t)]$ als '''Fouriertransformation''' und verwendet hierfür die Kurzschreibweise: | ||
| − | $X(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,x(t).$ | + | $$X(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,x(t).$$ |
Bei einem anklingenden Signal wird die Konvergenz allerdings nur dann erreicht, solange die Zeitfunktion weniger als exponentiell ansteigt. | Bei einem anklingenden Signal wird die Konvergenz allerdings nur dann erreicht, solange die Zeitfunktion weniger als exponentiell ansteigt. | ||
| Zeile 182: | Zeile 187: | ||
Wir betrachten eine akausale Sprungfunktion $x(t)$ = sign($t$) mit $x(t)$ = –1 für negative sowie $x(t)$ = +1 für positive Zeiten. Dieses Signal ist in nachfolgender Skizze links in blauer Farbe dargestellt. | Wir betrachten eine akausale Sprungfunktion $x(t)$ = sign($t$) mit $x(t)$ = –1 für negative sowie $x(t)$ = +1 für positive Zeiten. Dieses Signal ist in nachfolgender Skizze links in blauer Farbe dargestellt. | ||
| + | [[Datei:P_ID655__Sig_T_3_1_S6.png|250px|right| Sprungfunktion und Spektrum]] | ||
Da das Signal $x(t)$ nach beiden Seiten bis ins Unendliche reicht, muss zur Berechnung der Fouriertransformierten für beide Abschnitte zunächst ein geeigneter Konvergenzfaktor $\text{e}^{-\epsilon |t|}$ hinzugefügt werden (es gelte $\epsilon > 0$). Die resultierende Zeitfunktion lautet dann: | Da das Signal $x(t)$ nach beiden Seiten bis ins Unendliche reicht, muss zur Berechnung der Fouriertransformierten für beide Abschnitte zunächst ein geeigneter Konvergenzfaktor $\text{e}^{-\epsilon |t|}$ hinzugefügt werden (es gelte $\epsilon > 0$). Die resultierende Zeitfunktion lautet dann: | ||
| − | $x_\varepsilon (t) = \left\{ {\begin{array}{*{20}c} {{\rm{e}}^{ - \varepsilon t} } & {{\rm{f\ddot{u}r}}\quad t > 0,} \\ {{\rm{ - e}}^{\varepsilon t} } & {{\rm{f\ddot{u}r}}\quad t < 0.} \\\end{array}} \right.$ | + | $$x_\varepsilon (t) = \left\{ {\begin{array}{*{20}c} {{\rm{e}}^{ - \varepsilon t} } & {{\rm{f\ddot{u}r}}\quad t > 0,} \\ {{\rm{ - e}}^{\varepsilon t} } & {{\rm{f\ddot{u}r}}\quad t < 0.} \\\end{array}} \right.$$ |
Ähnlich wie auf der Seite Diracfunktion ergibt sich für die zugehörige Spektralfunktion | Ähnlich wie auf der Seite Diracfunktion ergibt sich für die zugehörige Spektralfunktion | ||
| − | $X_\varepsilon (f) = \frac{1}{{\varepsilon + {\rm{j}}2{\rm{\pi }}f}} - \frac{1}{{\varepsilon - {\rm{j}}2{\rm{\pi }}f}} = \frac{{ - {\rm{j4\pi }}f}}{{\varepsilon ^2 + \left( {2{\rm{\pi }}f} \right)^2 }}.$ | + | $$X_\varepsilon (f) = \frac{1}{{\varepsilon + {\rm{j}}2{\rm{\pi }}f}} - \frac{1}{{\varepsilon - {\rm{j}}2{\rm{\pi }}f}} = \frac{{ - {\rm{j4\pi }}f}}{{\varepsilon ^2 + \left( {2{\rm{\pi }}f} \right)^2 }}.$$ |
Eigentlich interessieren wir uns aber für das Spektrum der Sprungfunktion. Für diese gilt: | Eigentlich interessieren wir uns aber für das Spektrum der Sprungfunktion. Für diese gilt: | ||
| − | $x(t) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm}\to \hspace{0.05cm}0 } x_\varepsilon (t).$ | + | $$x(t) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm}\to \hspace{0.05cm}0 } x_\varepsilon (t).$$ |
Deshalb ist auch die Spektralfunktion $X(f)$ =F[$x(t)$] als Grenzwert von $X_\epsilon (f)$ für$\epsilon \to 0$ zu bestimmen: | Deshalb ist auch die Spektralfunktion $X(f)$ =F[$x(t)$] als Grenzwert von $X_\epsilon (f)$ für$\epsilon \to 0$ zu bestimmen: | ||
| − | $X(f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 } X_\varepsilon (f) = \frac{{ - {\rm{j}}}}{{{\rm{\pi }}f}} = \frac{1}{{{\rm{j\pi }}f}}.$ | + | $$X(f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 } X_\varepsilon (f) = \frac{{ - {\rm{j}}}}{{{\rm{\pi }}f}} = \frac{1}{{{\rm{j\pi }}f}}.$$ |
In der rechten Grafik ist die rein imaginäre Spektralfunktion $X(f)$ als blaue Kurve dargestellt. Man erkennt, dass mit zunehmender Frequenz $|X(f)|$ kontinuierlich abnimmt. | In der rechten Grafik ist die rein imaginäre Spektralfunktion $X(f)$ als blaue Kurve dargestellt. Man erkennt, dass mit zunehmender Frequenz $|X(f)|$ kontinuierlich abnimmt. | ||
Der grüne Kurvenzug in der linken Grafik zeigt das Signal $y(t)$, das sich von $x(t)$ nur bei den negativen Zeiten unterscheidet. In diesem Bereich gilt $y(t)$ = 0. Die zugehörige Spektralfunktion $Y(f)$ ist im gesamten Bereich nur halb so groß wie $X(f)$. Dies zeigt die nachfolgende Rechnung: | Der grüne Kurvenzug in der linken Grafik zeigt das Signal $y(t)$, das sich von $x(t)$ nur bei den negativen Zeiten unterscheidet. In diesem Bereich gilt $y(t)$ = 0. Die zugehörige Spektralfunktion $Y(f)$ ist im gesamten Bereich nur halb so groß wie $X(f)$. Dies zeigt die nachfolgende Rechnung: | ||
| − | $Y(f) = \mathop {\lim }\limits_{\varepsilon \to 0 } Y_\varepsilon (f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 }\frac{1}{{\varepsilon + {\rm{j}}2{\rm{\pi }}f}} = \frac{1}{{{\rm{j2\pi }}f}}.$ | + | $$Y(f) = \mathop {\lim }\limits_{\varepsilon \to 0 } Y_\varepsilon (f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 }\frac{1}{{\varepsilon + {\rm{j}}2{\rm{\pi }}f}} = \frac{1}{{{\rm{j2\pi }}f}}.$$ |
Zudem ergibt sich auf Grund des Gleichanteils nun noch eine Diracfunktion bei $f$ = 0 mit dem Gewicht 1/2. Hierauf wird im Beispiel zum Abschnitt Zuordnungssatz (Kapitel 3.3) noch im Detail eingegangen. | Zudem ergibt sich auf Grund des Gleichanteils nun noch eine Diracfunktion bei $f$ = 0 mit dem Gewicht 1/2. Hierauf wird im Beispiel zum Abschnitt Zuordnungssatz (Kapitel 3.3) noch im Detail eingegangen. | ||
| Zeile 210: | Zeile 216: | ||
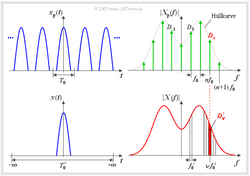
Bisher haben wir lediglich gezeigt, wie man für ein aperiodisches, impulsförmiges Signal $x(t)$ die zugehörige Spektralfunktion $X(f)$ berechnet. Nun wenden wir uns der umgekehrten Aufgabe zu, aus der Spektralfunktion $X(f)$ die Zeitfunktion $x(t)$ zu ermitteln. | Bisher haben wir lediglich gezeigt, wie man für ein aperiodisches, impulsförmiges Signal $x(t)$ die zugehörige Spektralfunktion $X(f)$ berechnet. Nun wenden wir uns der umgekehrten Aufgabe zu, aus der Spektralfunktion $X(f)$ die Zeitfunktion $x(t)$ zu ermitteln. | ||
| + | |||
| + | [[Datei:P_ID399__Sig_T_3_1_S7_rah.png|250px|right|Zum zweiten Fourierintegral]] | ||
Mit den gleichen Bezeichnungen wie auf den ersten Seiten dieses Kapitels kann man das Signal $x(t)$ als Fourierreihe schreiben, wobei nun der Grenzübergang $f_0' \to 0$ zu berücksichtigen ist: | Mit den gleichen Bezeichnungen wie auf den ersten Seiten dieses Kapitels kann man das Signal $x(t)$ als Fourierreihe schreiben, wobei nun der Grenzübergang $f_0' \to 0$ zu berücksichtigen ist: | ||
| − | $x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty}{D_{\it \nu}}' \cdot \rm e^{j 2 \pi \it\nu {f_{\rm 0}}' t}.$ | + | $$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty}{D_{\it \nu}}' \cdot \rm e^{j 2 \pi \it\nu {f_{\rm 0}}' t}.$$ |
Erweitert man nun sowohl den Zähler als auch den Nenner um $f_0'$, so erhält man: | Erweitert man nun sowohl den Zähler als auch den Nenner um $f_0'$, so erhält man: | ||
| − | $x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty} ({{D_{\it \nu}}'}/{{f_{\rm 0}}'}) \cdot \rm e^{j 2 \pi \it \nu {f_{\rm 0}}' t} \cdot {\it f_{\rm 0}}'.$ | + | $$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty} ({{D_{\it \nu}}'}/{{f_{\rm 0}}'}) \cdot \rm e^{j 2 \pi \it \nu {f_{\rm 0}}' t} \cdot {\it f_{\rm 0}}'.$$ |
Der Grenzübergang $f_0' \to 0$ hat nun folgende Auswirkungen: | Der Grenzübergang $f_0' \to 0$ hat nun folgende Auswirkungen: | ||
| Zeile 229: | Zeile 237: | ||
Ist die Spektralfunktion $X(f)$ eines aperiodischen und energiebegrenzten Signals gegeben, so lautet die dazugehörige '''Zeitfunktion''': | Ist die Spektralfunktion $X(f)$ eines aperiodischen und energiebegrenzten Signals gegeben, so lautet die dazugehörige '''Zeitfunktion''': | ||
| − | $x(t) = \hspace{0.01cm}\int_{-\infty} ^{{+}\infty} X(f) \, \cdot \, { \rm e}^{\rm j 2\pi \it ft} \,{\rm d}f$ | + | $$x(t) = \hspace{0.01cm}\int_{-\infty} ^{{+}\infty} X(f) \, \cdot \, { \rm e}^{\rm j 2\pi \it ft} \,{\rm d}f$$ |
| − | + | ⇒ '''Zweites Fourierintegral'''. | |
{{end}} | {{end}} | ||
| + | |||
| + | |||
==Aufgaben zu Kapitel 3.1== | ==Aufgaben zu Kapitel 3.1== | ||
Version vom 25. März 2016, 23:01 Uhr
Inhaltsverzeichnis
Eigenschaften aperiodischer Signale
Im letzten Kapitel haben wir periodische Signale betrachtet. Das wesentliche Charakteristikum dieser Signale ist, dass für sie eine Periodendauer $T_0$ angegeben werden kann. Ist eine solche Periodendauer nicht angebbar oder – was in der Praxis das gleiche ist – hat $T_0$ einen unendlich großen Wert, so spricht man von einem aperiodischen Signal. Für das gesamte Kapitel 3 sollen folgende Voraussetzungen gelten:
- Die betrachteten Signale $x(t)$ sind aperiodisch und energiebegrenzt, das heißt, sie besitzen nur eine endliche Energie $E_x$ und eine vernachlässigbar kleine (mittlere) Leistung $P_x$.
- Im Allgemeinen konzentriert sich die Energie dieser Signale auf einen relativ kurzen Zeitbereich, so dass man auch von impulsförmigen Signalen spricht.
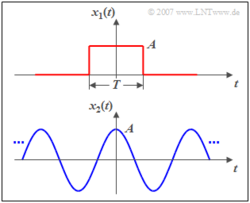
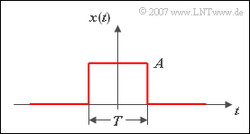
Das folgende Bild zeigt einen Rechteckimpuls $x_1(t)$ mit Amplitude $A$ und Dauer $T$ als Beispiel eines aperiodischen und zeitlich begrenzten Signals. Dieser besitzt eine endliche Signalenergie ($E_1=A^2 \cdot T$) und die Leistung $P_1$ = 0.
Ein leistungsbegrenztes Signal, z. B. das unten dargestellte Cosinussignal $x_1(t)$, besitzt dagegen
- stets eine endliche Leistung ($P_2=A^2/2$), und
- eine unendlich große Signalenergie ($E_2 \to \infty$).
Genauere Betrachtung der Fourierkoeffizienten
Wir gehen von einem periodischen Signal $x_P(t)$ mit der Periodendauer $T_0$ aus, das entprechend den Ausführungen im Kapitel 2.4 als (komplexe) Fourierreihe dargestellt werden kann:
$$x_{\rm P}(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j 2 \pi \hspace{-0.05cm}{\it n} \it t / T_{\rm 0}}.$$
Die Fourierkoeffizienten sind im Allgemeinen komplex, und es gilt $D_{-n}=D_n^\ast$:
$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} \it t / T_{\rm 0}}\, {\rm d}t.$$
Wie bereits im Kapitel 2.4 gezeigt wurde, ist die dazugehörige Spektralfunktion $X_p(f)$ ein so genanntes Linienspektrum mit Spektrallinien im Abstand $f_0=1/T_0$:
$$X_{\rm P}(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$
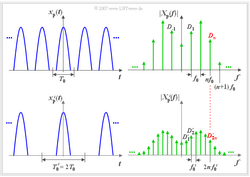
Das Bild zeigt links das periodische Zeitsignal und rechts das zugehörige Betragsspektrum.
Anzumerken ist, dass es sich hierbei lediglich um eine schematische Skizze handelt. Ist $x_P(t)$ eine reelle und gerade Funktion, so ist $X_P(f)$ ebenfalls reell und gerade. Die Gleichung $X_P(f) = |X_P(f)|$ gilt allerdings nur dann, wenn alle Spektrallinien zudem auch positiv sind.
Im unteren Bild ist ein weiteres periodisches Signal $x_P'(t)$ mit doppelter Periodendauer $T_0' = 2 \cdot T_0$ dargestellt. Bezüglich dieses Signals gilt:
$${x_{\rm P}}'(t)=\sum^{+\infty}_{n=-\infty}{\it D_n}'\cdot {\rm e}^{{\rm j} 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}'} \hspace{0.3cm}{\rm mit}\hspace{0.3cm}{\it D_n}'=\frac{1}{{T_0}'}\cdot \int^{{+T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}'}\, {\rm d}\it t.$$
Im Bereich von $-T_0/2$ bis $+t_0/2$ sind die beiden Signale identisch.
Betrachten wir auch hier die Spektralfunktion $X_P'(f)$: Aufgrund der doppelten Periodendauer ($T_0' = 2 \cdot T_0$) liegen nun die Spektrallinien enger beisammen ($f_0' = f_0/2$). Die beiden Koeffizienten $D_n$ und $D_{2n}'$ – im Bild rot hervorgehoben – gehören zur gleichen physikalischen Frequenz $f = n \cdot f_0 = 2n \cdot f_0'$.
Durch Analyse der Koeffizienten
$${D_{2n}}'=\frac{1}{{T_0}'}\cdot \int^{+{T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} \it t / {T_{\rm 0}}'}\, {\rm d}t$$
erkennen wir:
- Zwischen $T_0/2$ und $T_0'/2$ ist $x_P'(t)$ identisch 0, ebenso im dazu symmetrischen Intervall bei negativen Zeiten. Deshalb können die Integrationsgrenzen auf $\pm T_0/2$ eingeschränkt werden.
- Innerhalb der neuen Integrationsgrenzen kann $x_P'(t)$ durch $x_P(t)$ ersetzt werden.
Setzen wir nun in obiger Gleichung noch $T_0' = 2T_0$, so erhalten wir:
$${D_{2n}}'=\frac{1}{2T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} t / T_{\rm 0}}\, {\rm d}t = \frac{D_n}{2} .$$
Fassen wir dieses Ergebnis kurz zusammen:
- Die Spektrallinie des Signals $x_P'(t)$ bei der Frequenz $f = n \cdot f_0'$ wird mit $D_{2n}'$ bezeichnet (untere Grafik). Diese Linie ist genau halb so groß wie die Spektrallinie $D_n$ des Signals $x_P(t)$ bei der gleichen physikalischen Frequenz $f$ (obere Grafik).
- Die Spektralfunktion $X_P'(f)$ weist gegenüber $X_P(f)$ zusätzliche Spektrallinien bei $(n + 1/2) \cdot f_0$ auf. Diese führen dazu, dass im Zeitbereich jeder zweite Impuls von $x_P(t)$ um $n \cdot T_0$ gelegen ($n$ ungeradzahlig) ausgelöscht wird.
Vom periodischen zum aperiodischen Signal
Greifen wir nun die Überlegungen der vorherigen Seite auf und wählen die Periodendauer $T_0'$ von $x_P'(t)$ allgemein um einen ganzzahligen Faktor $k$ größer als die Periodendauer $T_0$ von $x_P(t)$. Dann können die bisherigen Aussagen verallgemeinert werden:
- Der Linienabstand ist bei $X_P'(f)$ um den Faktor $k$ geringer als beim Spektrum $X_P(f)$.
- Um diesen Sachverhalt hervorzuheben, bezeichnen wir die Frequenz-Laufvariable der Funktion $X_P'(f)$ mit $v$ anstelle von $n$. Es gilt: $v=k \cdot n$.
- Für die Spektrallinie des Signals $X_P'(f)$ bei der Frequenz $f=n \cdot f_0 = v \cdot f_0'$ gilt:
$${D_\nu}' = \frac{1}{k} \cdot D_n, \hspace{0.5cm} {\rm wobei} \hspace{0.5cm} \nu = k \cdot n .$$
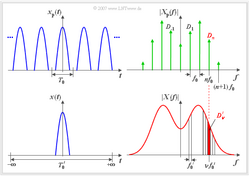
Wählt man nun – wie im Bild schematisch dargestellt – den Faktor $k$ und damit die Periodendauer $T_0'$ immer größer und lässt sie schließlich nach unendlich gehen, so
- geht das periodische Signal $x_P(t)$ in das aperiodische Signal $x(t)$ über,
- kann man das Linienspektrum $X_P(f)$ durch das kontinuierliche Spektrum $X(f)$ ersetzen.
Das erste Fourierintegral
Bezüglich den Spektralfunktion $X_P(f)$ und $X(f)$ lassen sich somit folgende Aussagen machen:
- Die einzelnen Spektrallinien liegen nun beliebig eng beieinander ($f_0'=1/T_0' \to 0$).
- In der Spektralfunktion $X(f)$ treten nun innerhalb bestimmter Intervalle alle möglichen (nicht nur diskrete) Frequenzen auf; $X(f)$ stellt also kein Linienspektrum mehr dar.
- Der Beitrag einer jeden einzelnen Frequenz $f$ zum Signal ist nur verschwindend gering ($k \to \infty, D_v' \to 0$). Aufgrund der unendlich vielen Frequenzen ergibt sich jedoch insgesamt ein endliches Resultat.
- Anstatt die Fourierkoeffizienten $D_v'$ zu berechnen, wird nun stattdessen eine spektrale Dichte $X(f)$ ermittelt. Bei der Frequenz $f=v \cdot f_0'$ gilt dann:
$$X(f = {\rm \nu} {f_{\rm 0}}') = \lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm} 0} ({{D_{\rm \nu}}'}/{{f_{\rm 0}}'}) = \lim_{{T_{\rm 0}}' \to \infty} ({D_{\rm \nu}}' \cdot {T_{\rm 0}}')$$ .
- Die Spektralfunktion (Dichte) $X(f)$ des aperiodischen Signals $x(t)$ ist im Spektrum $X_P(f)$ des vergleichbaren periodischen Signals $x_P(t)$ als Einhüllende erkennbar (siehe Grafiken).
- In der unteren Grafik entspricht $D_v'$ der rot hinterlegten Fläche des Frequenzintervalls um $v \cdot f_0'$ mit der Breite $f_0'$.
Verwendet man die auf der letzten Seite angegebenen Gleichungen, so erhält man:
$$X(f = {\rm \nu} \cdot {f_{\rm 0}}') = \lim_{{T_{\rm 0}'} \to \infty} \int ^{{T_{\rm 0}}'/2} _{-{T_{\rm 0}}'/2} x_{\rm P}(t) \, \cdot \, { \rm e}^{-\rm j 2\pi\nu \it {f_{\rm 0}}' t} \,{\rm d}t.$$
Durch den gemeinsamen Grenzübergang ($T_0' \to \infty, f_0' \to 0$) wird nun
- aus dem periodischen Signal $x_P(t)$ das aperiodische Signal $x(t)$, und
- aus der diskreten Frequenz $v \cdot f_0'$ die kontinuierliche Frequenzvariable $f$.
Damit erhält man eine fundamentale Definition, welche die Berechnung der Spektralfunktion einer aperiodischen Zeitfunktion ermöglicht. Der Name dieser Spektraltransformation geht auf den französischen Physiker Jean-Baptiste-Joseph Fourier zurück.
Die Spektralfunktion (oder kurz: das Spektrum) eines aperiodischen und gleichzeitig energiebegrenzten Signals $x(t)$ ist wie folgt zu berechnen:
$$X(f)= \hspace{0.05cm}\int \limits_{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t$$
⇒ Erstes Fourierintegral.
Das nachfolgende Lernvideo soll Ihnen die Aussagen der letzten Seiten nochmals verdeutlichen:
Unterschiede und Gemeinsamkeiten von kontinuierlichen und diskreten Spektren
(Dauer Teil 1: 6:20 – Teil 2: 5:15)
Beispiel zum ersten Fourierintegral
Gegeben ist der skizzierte Zeitverlauf $x(t)$. Gesucht ist das zugehörige Spektrum $X(f)$.
Wir wenden dazu das erste Fourierintegral an. Aus obiger Darstellung ist zu erkennen, dass das Signal $x(t)$ für $|t| > T/2$ gleich 0 ist. Das bedeutet, dass das Integrationsintervall auf den Bereich $\pm T/2$ begrenzt werden kann. Damit erhält man den Ansatz:
$$ \begin{align} X(f) & = A \int_{-T/2}^{+T/2} {\rm e}^{-{\rm j2\pi} ft}\,{\rm d}t = \frac{ A}{-\rm j2\pi f}\left[ {\rm e}^{-{\rm j}2\pi ft}\right]_{-T/2}^{+T/2} \\ & = \frac{\it A}{-\rm j 2\pi f}\left[\cos({\rm \pi} f T)-{\rm j} \cdot \sin({\rm \pi} fT)-\cos({\rm \pi} fT)-{\rm j} \cdot \sin({\rm \pi} fT)\right]. \end{align} $$
$$\Rightarrow X(f)=A\cdot \frac{\sin({\rm \pi} fT)}{{\rm \pi} f}.$$
Erweitert man Zähler und Nenner mit $T$, so erhält man:
$$X(f)=A\cdot T \cdot\frac{\sin(\pi fT)}{\pi fT} = A\cdot T \cdot{\rm si }(\pi fT) .$$
Die Funktion si($x$) = sin($x$)/$x$ wird auf der Seite Rechteckimpuls im Kapitel 3.2 noch eingehend analysiert. Man nennt sie ''si–Funktion'' oder auch ''Spaltfunktion''. <div style="clear:both;"> </div> </div> Betrachten wir noch die Einheiten der beiden Funktionen im Zeit- und Frequenzbereich: *Ist $x(t)$ beispielsweise eine Spannung, so hat die Impulsamplitude $A$ die Einheit „Volt”. *Die Dimension der Größe $T$ ist häufig die Zeit, z. B. mit der Einheit „Sekunde”. *Der Kehrwert der Zeit entspricht der Frequenz mit der Einheit „Hertz”. *Das Argument $f \cdot T$ ist dimensionslos. *Die Spektralfunktion hat somit beispielsweise die Einheit „V/Hz”. ==Fouriertransformation== Das Spektrum $X(f)$ eines Signals $x(t)$ lautet gemäß dem „Ersten Fourierintegral”: '"`UNIQ-MathJax14-QINU`"' Wie auf der letzten Seite an einem einfachen Beispiel gezeigt wurde, ist dieses Integral bei einem energiebegrenzten Signal $x(t)$ problemlos lösbar. Bei nicht energiebegrenzten Signalen, zum Beispiel *einem Gleichsignal (vgl. Kapitel 2.2), *einer harmonischen Schwingung (vgl. Kapitel 2.3), *einem anklingenden Signal, divergiert aber das Fourierintegral. Unter Einbeziehung einer beidseitig abfallenden Hilfsfunkion $\epsilon (t)$ kann allerdings die Konvergenz erzwungen werden: '"`UNIQ-MathJax15-QINU`"' Solche nicht energiebegrenzten Signale führen im Spektrum zu Diracfunktionen, manchmal auch „Distributionen” genannt. Man bezeichnet diesen allgemeinen Funktionalzusammenhang $X(f) = F[x(t)]$ als '''Fouriertransformation''' und verwendet hierfür die Kurzschreibweise: '"`UNIQ-MathJax16-QINU`"' Bei einem anklingenden Signal wird die Konvergenz allerdings nur dann erreicht, solange die Zeitfunktion weniger als exponentiell ansteigt. <div class="example"> Wir betrachten eine akausale Sprungfunktion $x(t)$ = sign($t$) mit $x(t)$ = –1 für negative sowie $x(t)$ = +1 für positive Zeiten. Dieses Signal ist in nachfolgender Skizze links in blauer Farbe dargestellt. [[Datei:P_ID655__Sig_T_3_1_S6.png|250px|right| Sprungfunktion und Spektrum]] Da das Signal $x(t)$ nach beiden Seiten bis ins Unendliche reicht, muss zur Berechnung der Fouriertransformierten für beide Abschnitte zunächst ein geeigneter Konvergenzfaktor $\text{e}^{-\epsilon |t|}$ hinzugefügt werden (es gelte $\epsilon > 0$). Die resultierende Zeitfunktion lautet dann: '"`UNIQ-MathJax17-QINU`"' Ähnlich wie auf der Seite Diracfunktion ergibt sich für die zugehörige Spektralfunktion '"`UNIQ-MathJax18-QINU`"' Eigentlich interessieren wir uns aber für das Spektrum der Sprungfunktion. Für diese gilt: '"`UNIQ-MathJax19-QINU`"' Deshalb ist auch die Spektralfunktion $X(f)$ =F[$x(t)$] als Grenzwert von $X_\epsilon (f)$ für$\epsilon \to 0$ zu bestimmen: '"`UNIQ-MathJax20-QINU`"' In der rechten Grafik ist die rein imaginäre Spektralfunktion $X(f)$ als blaue Kurve dargestellt. Man erkennt, dass mit zunehmender Frequenz $|X(f)|$ kontinuierlich abnimmt. Der grüne Kurvenzug in der linken Grafik zeigt das Signal $y(t)$, das sich von $x(t)$ nur bei den negativen Zeiten unterscheidet. In diesem Bereich gilt $y(t)$ = 0. Die zugehörige Spektralfunktion $Y(f)$ ist im gesamten Bereich nur halb so groß wie $X(f)$. Dies zeigt die nachfolgende Rechnung: '"`UNIQ-MathJax21-QINU`"' Zudem ergibt sich auf Grund des Gleichanteils nun noch eine Diracfunktion bei $f$ = 0 mit dem Gewicht 1/2. Hierauf wird im Beispiel zum Abschnitt Zuordnungssatz (Kapitel 3.3) noch im Detail eingegangen. <div style="clear:both;"> </div> </div> =='"`UNIQ--h-5--QINU`"'Das zweiter Fourierintegral== Bisher haben wir lediglich gezeigt, wie man für ein aperiodisches, impulsförmiges Signal $x(t)$ die zugehörige Spektralfunktion $X(f)$ berechnet. Nun wenden wir uns der umgekehrten Aufgabe zu, aus der Spektralfunktion $X(f)$ die Zeitfunktion $x(t)$ zu ermitteln. [[Datei:P_ID399__Sig_T_3_1_S7_rah.png|250px|right|Zum zweiten Fourierintegral]] Mit den gleichen Bezeichnungen wie auf den ersten Seiten dieses Kapitels kann man das Signal $x(t)$ als Fourierreihe schreiben, wobei nun der Grenzübergang $f_0' \to 0$ zu berücksichtigen ist: '"`UNIQ-MathJax22-QINU`"' Erweitert man nun sowohl den Zähler als auch den Nenner um $f_0'$, so erhält man: '"`UNIQ-MathJax23-QINU`"' Der Grenzübergang $f_0' \to 0$ hat nun folgende Auswirkungen: *Die (unendliche) Summe wird zu einem Integral, wobei $f_0'$ formal durch die differenzielle Größe d$f$ (Integrationsvariable) zu ersetzen ist. *Die Größe $v \cdot f_0'$ im Exponenten beschreibt die physikalische Frequenz $f$. *Der Quotient $D_v'/f_0'$ ergibt die Spektralfunktion $X(f)$ bei der Frequenz $f$. Unter Berücksichtigung dieser Eigenschaften kommt man zum ''zweiten Fourierintegral''. <div class="definition"> Ist die Spektralfunktion $X(f)$ eines aperiodischen und energiebegrenzten Signals gegeben, so lautet die dazugehörige Zeitfunktion:
$$x(t) = \hspace{0.01cm}\int_{-\infty} ^{{+}\infty} X(f) \, \cdot \, { \rm e}^{\rm j 2\pi \it ft} \,{\rm d}f$$
⇒ Zweites Fourierintegral.