Aufgaben:Aufgabe 5.3Z: Zero-Padding: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 68: | Zeile 68: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' Bereits mit $N = 128$ ist $ | + | '''1.''' Bereits mit $N = 128$ ist $T_{\rm P} = 1.28 \cdot T$, also größer als die Breite des Rechtecks. Somit spielt hier der Abbruchfehler überhaupt keine Rolle. Der MQF–Wert wird allein durch den Aliasingfehler bestimmt. Die Zahlenwerte bestätigen eindeutig, dass MQF (nahezu) unabhängig von $N$ ist. Richtig sind somit die <u>Lösungsvorschläge 1 und 3</u>. |
| − | '''2.''' Aus $ | + | '''2.''' Aus $T_{\rm A}/T = 0.01$ folgt $f_{\rm P} \cdot T = 100$. Die Stützwerte von $X(f)$ liegen im Bereich $–50 ≤ f \cdot T < 50$. Für den Abstand zweier Abtastwerte im Frequenzbereich gilt $f_{\rm A} = f_{\rm P}/N$. Daraus ergeben sich folgende Ergebnisse: |
| + | *$N = 128$: $f_{\rm A} \cdot T \; \underline{\approx 0.781}$, | ||
| + | *$N = 512$: $f_{\rm A} \cdot T \; \underline{\approx 0.196}$. | ||
| − | |||
| − | ''' | + | '''3.''' Für $N = 128$ ergibt sich für das Produkt $\text{MQF} \cdot f_{\rm A} \approx 4.7 \cdot 10^{–6}/T$. Für $N = 512$ ist das Produkt etwa um den Faktor 4 kleiner. Das heißt: |
| + | *Durch „Zero–Padding” wird keine größere DFT-Genauigkeit erzielt, dafür aber eine feinere „Auflösung” des Frequenzbereichs. | ||
| + | *Das Produkt $\text{MQF} \cdot f_{\rm A}$ berücksichtigt diese Tatsache; es sollte stets möglichst klein sein. Richtig ist die <u>erste Aussage</u>. | ||
| − | '''5.''' <u>Alle Aussagen treffen zu</u> | + | |
| + | '''4.''' Wegen $T_{\rm A} \cdot f_{\rm A} \cdot N = 1$ ergibt sich bei konstantem $N$ immer dann ein kleinerer $f_{\rm A}$–Wert, wenn man $T_{\rm A}$ vergrößert. | ||
| + | *Aus der Tabelle auf der Angabenseite erkennt man, dass damit der mittlere quadratische Fehler MQF signifikant (um den Faktor $400$) vergrößert wird. | ||
| + | *Dieser Effekt ist auf die Zunahme des Aliasingfehlers zurückzuführen, da durch den Übergang von $T_{\rm A}/T = 0.01$ auf $T_{\rm A}/T = 0.05$ die Frequenzperiode um den Faktor $5$ kleiner wird. | ||
| + | *Der Abbruchfehler spielt dagegen beim Rechteckimpuls weiterhin keine Rolle, solange $T_{\rm P} = N \cdot T_{\rm A}$ größer ist als die Impulsdauer $T$. | ||
| + | Richtig sind somit die <u>Lösungsvorschläge 1 und 4</u>. | ||
| + | |||
| + | '''5.''' <u>Alle Aussagen treffen zu</u>: | ||
| + | * Mit den Parameterwerten $N = 64$ und $T_{\rm A}/T = 0.01$ tritt ein extrem großer Abbruchfehler auf. | ||
| + | *Alle Zeitkoeffizienten sind hier $1$, so dass die DFT fälschlicherweise ein Gleichsignal anstelle der Rechteckfunktion interpretiert. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 24. Januar 2017, 14:11 Uhr
Wir betrachten die DFT eines Rechteckimpulses $x(t)$ der Höhe $1$ und der Dauer $T$. Damit hat die Spektralfunktion $X(f)$ einen $\sin(f)/f$–förmigen Verlauf.
Für diesen Sonderfall soll der Einfluss des DFT–Parameters $N$ analysiert werden, wobei der Stützstellenabstand im Zeitbereich stets $T_{\rm A} = 0.01T$ bzw. $T_{\rm A} = 0.05T$ betragen soll.
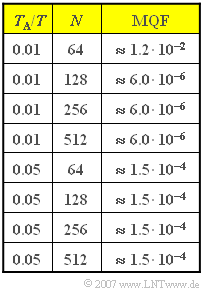
Nebenstehend sind für unterschiedliche Werte von $N$ die sich ergebenden Werte für den mittleren quadratischen Fehler (MQF) der Stützwerte im Frequenzbereich angegeben:
- $${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$
Für $T_A/T = 0.01$ sind somit stets $101$ der DFT–Koeffizienten $d(ν)$ von 0 verschieden.
- Davon besitzen $99$ den Wert $1$ und die beiden Randkoeffizienten sind jeweils gleich $0.5$.
- Vergrößert man $N$, so wird das DFT–Koeffizientenfeld mit Nullen aufgefüllt. Man spricht von „Zero–Padding”.
Hinweise:
- Die Aufgabe gehört zum Kapitel Fehlermöglichkeiten bei Anwendung der DFT.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Die Theorie zu diesem Kapitel ist auch im folgenden Lernvideo zusammengefasst:
Fragebogen
Musterlösung
1. Bereits mit $N = 128$ ist $T_{\rm P} = 1.28 \cdot T$, also größer als die Breite des Rechtecks. Somit spielt hier der Abbruchfehler überhaupt keine Rolle. Der MQF–Wert wird allein durch den Aliasingfehler bestimmt. Die Zahlenwerte bestätigen eindeutig, dass MQF (nahezu) unabhängig von $N$ ist. Richtig sind somit die Lösungsvorschläge 1 und 3.
2. Aus $T_{\rm A}/T = 0.01$ folgt $f_{\rm P} \cdot T = 100$. Die Stützwerte von $X(f)$ liegen im Bereich $–50 ≤ f \cdot T < 50$. Für den Abstand zweier Abtastwerte im Frequenzbereich gilt $f_{\rm A} = f_{\rm P}/N$. Daraus ergeben sich folgende Ergebnisse:
- $N = 128$: $f_{\rm A} \cdot T \; \underline{\approx 0.781}$,
- $N = 512$: $f_{\rm A} \cdot T \; \underline{\approx 0.196}$.
3. Für $N = 128$ ergibt sich für das Produkt $\text{MQF} \cdot f_{\rm A} \approx 4.7 \cdot 10^{–6}/T$. Für $N = 512$ ist das Produkt etwa um den Faktor 4 kleiner. Das heißt:
- Durch „Zero–Padding” wird keine größere DFT-Genauigkeit erzielt, dafür aber eine feinere „Auflösung” des Frequenzbereichs.
- Das Produkt $\text{MQF} \cdot f_{\rm A}$ berücksichtigt diese Tatsache; es sollte stets möglichst klein sein. Richtig ist die erste Aussage.
4. Wegen $T_{\rm A} \cdot f_{\rm A} \cdot N = 1$ ergibt sich bei konstantem $N$ immer dann ein kleinerer $f_{\rm A}$–Wert, wenn man $T_{\rm A}$ vergrößert.
- Aus der Tabelle auf der Angabenseite erkennt man, dass damit der mittlere quadratische Fehler MQF signifikant (um den Faktor $400$) vergrößert wird.
- Dieser Effekt ist auf die Zunahme des Aliasingfehlers zurückzuführen, da durch den Übergang von $T_{\rm A}/T = 0.01$ auf $T_{\rm A}/T = 0.05$ die Frequenzperiode um den Faktor $5$ kleiner wird.
- Der Abbruchfehler spielt dagegen beim Rechteckimpuls weiterhin keine Rolle, solange $T_{\rm P} = N \cdot T_{\rm A}$ größer ist als die Impulsdauer $T$.
Richtig sind somit die Lösungsvorschläge 1 und 4.
5. Alle Aussagen treffen zu:
- Mit den Parameterwerten $N = 64$ und $T_{\rm A}/T = 0.01$ tritt ein extrem großer Abbruchfehler auf.
- Alle Zeitkoeffizienten sind hier $1$, so dass die DFT fälschlicherweise ein Gleichsignal anstelle der Rechteckfunktion interpretiert.
