Aufgabe 4.6: OVSF-Codes

• Zurück zum Buch

Baumstruktur zur Konstruktion
eines OVSF–Codes

Die Spreizcodes für UMTS sollen

• alle zueinander orthogonal sein, um gegenseitige Beeinflussung der Teilnehmer zu vermeiden,
• möglichst flexibel sein, um unterschiedliche Spreizfaktoren  $J$  zu realisieren.

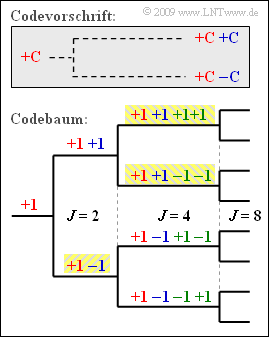
Ein Beispiel hierfür sind die so genannten  Codes mit variablem Spreizfaktor  (englisch:  Orthogonal Variable Spreading Factor,  OVSF), die Spreizcodes der Längen von  $J = 4$  bis  $J = 512$  bereitstellen. Diese können, wie in der Grafik zu sehen ist, mit Hilfe eines Codebaums erstellt werden. Dabei entstehen bei jeder Verzweigung aus einem Code  $\mathcal{C}$  zwei neue Codes

• $(+\mathcal{C} \ +\hspace{-0.05cm}\mathcal{C})$,
• $(+\mathcal{C}\ -\hspace{-0.05cm}\mathcal{C})$.

Die Grafik verdeutlicht das hier angegebene Prinzip am Beispiel  $J = 4$.

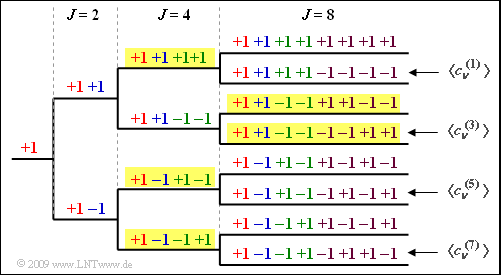
Nummeriert man die Spreizfolgen von  $0$  bis  $J –1$  durch, so ergeben sich hier die Spreizfolgen

$$\langle c_\nu^{(0)}\rangle \ = \ {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle c_\nu^{(2)}\rangle \ = \ {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(3)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$

Nach dieser Nomenklatur gibt es für den Spreizfaktor  $J = 8$  die Spreizfolgen  $\langle c_{\nu}^{(0)} \rangle, \ \text{...} \ ,\langle c_{\nu}^{(7)} \rangle$.

Anzumerken ist, dass kein Vorgänger und Nachfolger eines Codes von anderen Teilnehmern benutzt werden darf.

• Im Beispiel könnten also vier Spreizcodes mit dem Spreizfaktor  $J = 4$  verwendet werden, oder
• die drei gelb hinterlegten Codes – einmal mit  $J = 2$  und zweimal mit  $J = 4$.

Hinweise:

• Die Aufgabegehört zum Kapitel  Nachrichtentechnische Aspekte von UMTS.
• Bezug genommen wird insbesondere auf die Seite  Spreizcodes und Verwürfelung bei UMTS.

Fragebogen

1

Konstruieren Sie das Baumdiagramm für  $J = 8$. Welche OVSF–Codes ergeben sich daraus?

	$\langle c_{\nu}^{(1)} \rangle = +1 +1 +1 +1 –1 –1 –1 –1$,
	$\langle c_{\nu}^{(3)} \rangle = +1 +1 –1 –1 +1 +1 –1 –1$,
	$\langle c_{\nu}^{(5)} \rangle = +1 –1 +1 –1 –1 +1 –1 +1$,
	$\langle c_{\nu}^{(7)} \rangle = +1 –1 –1 +1 –1 +1 +1 –1$.

2

Wieviele UMTS–Teilnehmer können mit  $J = 8$  maximal bedient werden?

$K_{\rm max} \ = \ $

3

Wieviele Teilnehmer können versorgt werden, wenn drei von ihnen einen Spreizcode mit  $J = 4$  verwenden sollen?

$K \ = \ $

4

Gehen Sie von einer Baumstruktur für  $J = 32$  aus. Ist die folgende Zuweisung machbar:
Zweimal  $J = 4$, einmal  $J = 8$, zweimal  $J = 16$,  achtmal $J = 32$ ?

	Ja.
	Nein.

Musterlösung

Musterlösung

OVSF–Baumstruktur für  $J = 8$

(1)  Die Grafik zeigt die OVSF–Baumstruktur für  $J = 8$  Nutzer.

• Daraus ist ersichtlich, dass die Lösungsvorschläge 1, 3 und 4 zutreffen, nicht jedoch der zweite.

(2)  Wird jedem Nutzer ein Spreizcode mit  $J = 8$  zugewiesen, so können  $\underline{K_{\rm max} = 8}$  Teilnehmer versorgt werden.

(3)  Wenn drei Teilnehmer mit  $J = 4$  versorgt werden, können nur mehr zwei Teilnehmer durch eine Spreizfolge mit  $J = 8$  bedient werden (siehe beispielhafte gelbe Hinterlegung in obiger Grafik)   ⇒   $\underline{K = 5}$.

(4)  Wir bezeichnen mit

• $K_{4} = 2$  die Anzahl der Spreizfolgen mit  $J = 4$,
• $K_{8} = 1$  die Anzahl der Spreizfolgen mit  $J = 8$,
• $K_{16} = 2$  die Anzahl der Spreizfolgen mit  $J = 16$,
• $K_{32} = 8$  die Anzahl der Spreizfolgen mit  $J = 32$.

Dann muss folgende Bedingung erfüllt sein:

$$K_4 \cdot \frac{32}{4} + K_8 \cdot \frac{32}{8} +K_{16} \cdot \frac{32}{16} +K_{32} \cdot \frac{32}{32} \le 32 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K_4 \cdot8 + K_8 \cdot 4 +K_{16} \cdot 2 +K_{32} \cdot1 \le 32 \hspace{0.05cm}.$$

• Wegen  $2 \cdot 8 + 1 \cdot 4 + 2 \cdot 2 + 8 = 32$  ist die gewünschte Belegung gerade noch erlaubt   ⇒   Antwort JA.
• Die zweimalige Bereitstellung des Spreizgrads  $J = 4$  blockiert zum Beispiel die obere Hälfte des Baums, nach der Versorgung der einen Spreizung mit  $J = 8$, bleiben auf der  $J = 8$–Ebene noch drei der acht Äste zu belegen, usw. und so fort.