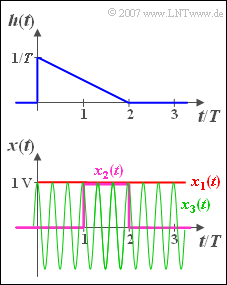
Die Impulsantwort eines LZI-Systems hat im Zeitbereich zwischen $0$ und $2T$ den folgenden Verlauf:
- $$h( t ) = \frac{1}{T}\cdot \left( {1 - \frac{t}{ {2T}}} \right).$$
Außerhalb dieses Intervalls ist $h(t) = 0$. Die zugehörige Spektralfunktion lautet:
- $$H( f ) = \frac{1}{ {8\left( {{\rm{\pi }}fT} \right)^2 }} \cdot \left( {1 - {\rm{j \cdot 4\pi }}fT - {\rm{e}}^{ - {\rm{j \hspace{0.05cm}\cdot \hspace{0.05cm} 4\pi }}\hspace{0.05cm}f\hspace{0.05cm}T} } \right).$$
Zur Berechnung des so genannten „Gleichsignalübertragungsfaktors” ⇒ $H(f = 0)$ ist diese Gleichung nicht geeignet, da sowohl der Klammerausdruck als auch der Nenner Null werden. Es gilt aber auch:
- $$H( {f = 0} ) = \int_0^{2T} {h( t )\hspace{0.1cm}{\rm d}t = 1.}$$
An den Eingang dieses Filters werden drei verschiedene Zeitsignale angelegt (siehe Skizze):
- $x_1(t)$ ist ein Gleichsignal mit der Höhe $x_0 = 1 \hspace{0.05cm}{\rm V}$.
- $x_2(t)$ ist ein Rechteckimpuls mit der Dauer $T$ und der Höhe $x_0 = 1\hspace{0.05cm} {\rm V}$, beginnend bei $t = T$.
- $x_3(t)$ ist ein Cosinussignal mit der Frequenz $f_0 = 3/T$ und der Amplitude $x_0 = 1 \hspace{0.05cm}{\rm V}$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Faltungssatz und Faltungsoperation.
- Die Thematik dieses Abschnitts wird auch im interaktiven Applet Zur Verdeutlichung der grafischen Faltung veranschaulicht.
Fragebogen
Musterlösung
- $x_1(t)$ und $x_3(t)$ beinhalten jeweils nur eine Frequenz, nämlich $f = 0$ bzw. $f = f_0$. Hier ist jeweils der Umweg über das Spektrum vorzuziehen.
- Beim Rechtecksignal $x_2(t)$ ist die Berechnung über die Faltung günstiger, da die Fourierrücktransformation von $Y_2(f)$ kompliziert ist.
(2) Beim Eingangssignal $x_1(t)$ ist das Ausgangssignal ebenfalls ein Gleichsignal, da folgende Gleichungen gelten:
- $$Y_1 (f) = X_1 (f) \cdot H(f)\quad {\rm{mit}}\quad X_1 (f) = 1\;{\rm{V}} \cdot \delta (f)$$
- $$ \Rightarrow Y_1 (f) = 1\;{\rm{V}} \cdot \delta (f) \cdot H( {f = 0} ) = 1\;{\rm{V}} \cdot \delta (f) \; \Rightarrow \; y_1 (t) = 1\;{\rm{V}} \cdot H( {f = 0} ) \hspace{0.15 cm}\underline{= 1\;{\rm{V}}}.$$
- Die Berechnung über die Faltung führt zum gleichen Ergebnis, wenn man berücksichtigt, dass das Integral über die Impulsantwort im vorliegenden Fall gleich $1$ ist.
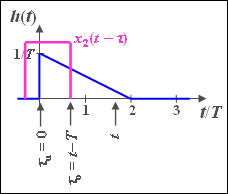
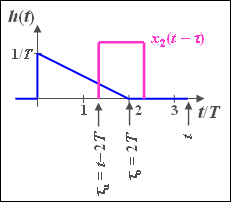
(3) Das gespiegelte Signal $x_2(-t)$ hat Signalanteile zwischen $-2T$ und $-T$.
- Erst eine Verschiebung um $T \hspace{-0.1cm}+ \hspace{-0.1cm}\varepsilon$ führt zu einer Überlappung mit $h(t)$. Hierbei bezeichnet $\varepsilon$ eine beliebig kleine, aber positive Zeit.
- Ist die Verschiebung allerdings größer als $4T\hspace{-0.1cm} - \hspace{-0.1cm}\varepsilon$, so liefert die Integration über das Produkt ebenfalls den Wert Null. Daraus folgt:
- $$t_{\text{min}} \;\underline{= T}, \ \ \ t_{\text{max}} \;\underline{= 4T}.$$
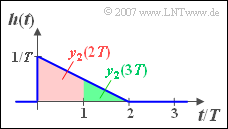
(4) Das Ergebnis der grafischen Faltung für die Zeiten $t = 2T$ und $t = 3T$ kann man nebenstehender Skizze entnehmen.
- Der Wert bei $t = 2T$ entspricht der rötlich unterlegten Fläche:
- $$y_2( {t = 2T} ) = \frac{1}{2}\cdot ( {\frac{1}{T} + \frac{1}{ {2T}}} ) \cdot T \cdot x_0 \hspace{0.15 cm}\underline{= 0.75 {\rm V}} .$$
- Die grün unterlegte Fläche kennzeichnet den Wert bei $t = 3T$:
- $$y_2( {t = 3T} ) = \frac{1}{2}\cdot ( {\frac{1}{2T} + 0} ) \cdot T \cdot x_0 \hspace{0.15 cm}\underline{= 0.25 {\rm V}} .$$
Um den gesamten Signalverlauf zwischen $t = T$ und $t = 4T$ zu berechnen, müssen drei Bereiche getrennt betrachtet werden. Zur Vereinfachung der Darstellung wird im Folgenden $x_0 = 1$ gesetzt ⇒ Amplitudennormierung.
(4a) Für $T \leq t \leq 2T$ liegt die untere Grenze bei $τ_u = 0$, die obere Grenze bei $τ_0 = t - T$:
- $$y_2 (t) = \int_{\tau _u }^{\tau _0 } {h(\tau )\,{\rm{d}}\tau = \int_0^{t - T} {\frac{1}{T}} }\cdot \left( {1 - \frac{\tau }{ {2T}}} \right)\,{\rm{d}}\tau .$$
- Mit dem unbestimmten Integral $I(\tau ) = {\tau }/{T} - 0.25 \cdot \left( {{\tau }/{T}} \right)^2$ ergibt sich
- $$y_2 (t) = I(t - T) - I(0) = \frac{ {t - T}}{T} - 0.25 \cdot \left( {\frac{ {t - T}}{T}} \right)^2 $$
- $$\Rightarrow \hspace{0.3cm}y_2 (t) = 1.5 \cdot {t}/{T} - 0.25\cdot \left( {{t}/{T}} \right)^2 - 1.25.$$
- Zur Verifizierung betrachten wir die beiden Grenzen. Man erhält die Werte $y_2(T) = 0$ und $y_2(2T) = 0.75$.
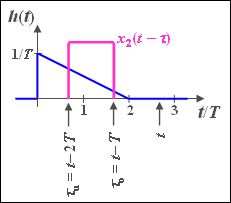
(4b) Im Intervall $2T \leq t \leq 3T$ gilt weiterhin $τ_0 = t - T$, während nun $τ_u = t - 2T$ ist:
- $$y_2 (t) = I(t - T) - I(t - 2T) = 1.75 - 0.5 \cdot {t}/{T}.$$
- Dies entspricht einem linearen Abfall mit den beiden Grenzwerten
- $$y_2(2T) = 0.75,$$
- $$y_2(3T) = 0.25.$$
(4c) Für das Intervall $3T \leq t \leq 4T$ gilt $τ_0 = 2T$ und $τ_u = t - 2T$:
- $$y_2 (t) = I(2T) - I(t - 2T) = - 2 \cdot {t}/{T} + 0.25\left( {c{t}/{T}} \right)^2 + 4.$$
- Auch hier ergeben sich die richtigen Grenzwerte:
- $$y_2 (3T) = 0.25,$$
- $$y_2 (4T) = 0.$$
(5) Diese Teilaufgabe könnte prinzipiell auch direkt mit der Faltung gelöst werden.
- Da $x_3(t)$ aber eine gerade Funktion ist, kann hier nun auf die Spiegelung verzichtet werden und man erhält:
- $$y_3 (t) = \int_{ - \infty }^{ + \infty } {h(\tau ) \cdot x_3 (t + \tau )\hspace{0.1cm}{\rm{d}}\tau = x_0 }\cdot \int_0^{2T} {h(\tau ) \cdot \cos (2{\rm{\pi }}f_0 (t + \tau )\hspace{0.1cm}{\rm{d}}\tau .}$$
- Einfacher ist hier der Weg über die Spektren. $X(f)$ besteht aus zwei Diraclinien bei $\pm 3f_0$. Somit muss nur für diese Frequenz der Frequenzgang berechnen:
- $$H( {f = 3f_0 } ) = \frac{1}{ {72{\rm{\pi }}^{\rm{2}} }}\big[ {1 - {\rm{j}}\cdot 12{\rm{\pi }} - {\rm{cos}}( {{\rm{12\pi }}} ) + {\rm{j}}\cdot \sin ( {{\rm{12\pi }}})} \big] = \frac{1}{ {72{\rm{\pi }}^{\rm{2}} }}\big[ 1 - {\rm j}\cdot 12{\rm \pi } - 1 + {\rm j}\cdot 0 \big]= { - {\rm{j}}} \cdot \frac{1}{ {6{\rm{\pi }}}}.$$
- Das Spektrum des Ausgangssignals lautet:
- $$Y(f) = - {\rm{j}} \cdot \frac{ {x_0 }}{{{\rm{12\pi }}}}\cdot \delta \left( {f - 3f_0 } \right) + {\rm{j}} \cdot \frac{ {x_0 }}{{{\rm{12\pi }}}}\cdot \delta \left( {f + 3f_0 } \right).$$
- Das Signal $y_3(t)$ ist somit sinusförmig mit der Amplitude $x_0/(6\pi )$.
- Bei $t = 0$ ergibt sich der Signalwert $y_3(t = 0)\; \underline{= 0}$.