Aufgabe 3.8: Decision Feedback Equalization mit Laufzeitfilter

• Zurück zum Buch

Entscheidungsrückkopplung mit Laufzeitfilter

Wir betrachten ein bipolares Binärsystem mit Entscheidungsrückkopplung  $($englisch:  "Decision Feedback Equalization",  $\rm DFE)$.

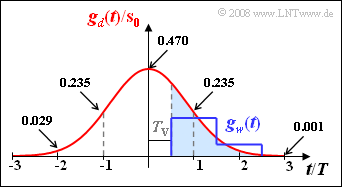
Der vorentzerrte Grundimpuls  $g_d(t)$  kann als Rechteckantwort eines Gaußtiefpasses mit der Grenzfrequenz  $f_{\rm G} \cdot T = 0.25$  berechnet werden und ist in der Grafik rot eingezeichnet. Bei der  Aufgabe 3.8Z  sind die Abtastwerte von  $g_d(t)$  tabellarisch im Abstand  $T/10$  angegeben.

Bei idealer Entscheidungsrückkopplung – dimensioniert für den Detektionszeitpunkt  $T_{\rm D} = 0$  – gilt:

• Es wird ein Kompensationsimpuls  $g_w(t)$  gebildet,  der für  $t ≥ T_{\rm V} = T/2$  gleich  $g_d(t)$  und für  $t < T_{\rm V}$  identisch Null ist  (blau gefüllte Fläche).

• Der korrigierte Grundimpuls  $g_k(t) = g_d(t) - g_w(t)$  ist somit für  $t > T/2$  stets Null.

Durch eine Simulation wurde für dieses System mit idealer DFE das ungünstigste S/N–Verhältnis am Entscheider und daraus die worst–case–Fehlerwahrscheinlichkeit bestimmt,  wobei die Detektion zum Zeitpunkt  $T_{\rm D} = 0$  erfolgte.  Es ergab sich folgendes Ergebnis:

$$\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2\big]^2}{ \sigma_d^2} = 25 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 14\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q}(\sqrt{\rho_{\rm U}}) \approx 2.9 \cdot 10^{-7} \hspace{0.05cm}.$$

Eine aufwandsgünstige analoge Realisierung der DFE ist mit einem Laufzeitfilter möglich.  In der Grafik ist der Kompensationsimpuls  $g_w(t)$  für ein solches Laufzeitfilter mit der Ordnung  $N = 2$  und den Koeffizienten  $k_1 = 0.2$  und  $k_2 = 0.05$  eingezeichnet  (blaue Kurve).

Hinweis:  Die Aufgabe gehört zum Kapitel  "Entscheidungsrückkopplung".

Fragebogen

1

Wie groß ist die (normierte) halbe Augenöffnung bei idealer DFE?  Auch für die weiteren Aufgaben gelte  $T_{\rm D} = 0$.

$\ddot{o}(T_{\rm D})/(2s_0) \ = \ $

2

Berechnen Sie aus dem angegebenen SNR den (normierten) Störeffektivwert.

$\sigma_d/s_0\ = \ $

3

Berechnen Sie die halbe normierte Augenöffnung und den Störabstand,  wenn die DFE durch ein Laufzeitfilter mit  $N = 2$,  $k_1 = 0.2$  und  $k_2 = 0.05$  realisiert wird.

$\ddot{o}(T_{\rm D})/(2s_0) \ = \ $

$10 \cdot {\rm lg} \, \rho_{\rm U} \ = \ $ $\ \rm dB$

4

Berechnen Sie die halbe normierte Augenöffnung und den Störabstand mit  $N = 2$,  wenn die Koeffizientn  $k_1$  und  $k_2$  bestmöglichst gewählt werden?

$\ddot{o}(T_{\rm D})/(2s_0) \ = \ $

$10 \cdot {\rm lg} \, \rho_{\rm U} \ = \ $ $\ \rm dB$

5

Welche der folgenden Aussagen sind im vorliegenden Fall zutreffend?

	Bei einem Empfänger ohne DFE ist das Auge geschlossen.
	Ein Nachteil der DFE ist die Fehlerfortpflanzung
	Durch die DFE wird jede einzelne Symbolentscheidung verbessert.

Musterlösung

Musterlösung

(1)  Bei idealer DFE werden alle Nachläufer kompensiert.  Somit erhält man für die halbe Augenöffnung unter der Voraussetzung  $T_{\rm D} = 0$:

$$\frac{\ddot{o}(T_{\rm D})}{ 2} = g_d(0) - g_d(-T)- g_d(-2T)- g_d(-3T)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = 0.470 - 0.235 - 0.029 -0.001\hspace{0.15cm}\underline { = 0.205} \hspace{0.05cm}.$$

(2)  Aus dem angegebenen ungünstigsten S/N–Verhältnis  $\rho_{\rm U} = 25$  folgt:

$$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2} = 25 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} (\sigma_d/s_0)^2 = \frac{[\ddot{o}(T_{\rm D})/(2s_0)]^2}{ 25}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma_d/s_0 = \frac{\ddot{o}(T_{\rm D})/(2s_0)}{ 5} \hspace{0.15cm}\underline {= 0.041} \hspace{0.05cm}.$$

(3)  Durch dieses Filter werden die beiden ersten Nachläufer nur teilweise und der dritte Nachläufer gar nicht kompensiert.

• Daraus folgt mit dem Ergebnis der Teilaufgabe  (1):

$$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} \ = \ 0.205 - | 0.235 - 0.2 | - |0.029 -0.05 | -0.001 = 0.205 - 0.035 - 0.021 -0.001 \hspace{0.15cm}\underline {= 0.148}$$

$$\Rightarrow \hspace{0.3cm} \rho_{\rm U} =\frac{0.148^2}{ 0.041^2} \approx 13 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U}\hspace{0.15cm}\underline { \approx 11.1\,{\rm dB}} \hspace{0.05cm}.$$

(4)  Es ergeben sich nahezu die gleichen Ergebnisse wie bei idealer DFE  (lediglich der dritte Nachläufer wird nicht kompensiert):

$$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0}\hspace{0.15cm}\underline { = 0.204} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 13.94 \,{\rm dB}}\hspace{0.3cm}{\rm (Ideale \hspace{0.15cm}DFE\hspace{-0.15cm}:}\hspace{0.15cm}{13.98 \,{\rm dB)}} \hspace{0.05cm}.$$

(5)  Die  beiden ersten Aussagen  sind richtig:

• Ohne DFE beträgt die halbe Augenöffnung:

$$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = 0.470 - 2 \cdot 0.235 - 2 \cdot 0.029 - 2 \cdot 0.001 < 0 \hspace{0.05cm}.$$

• Wird irgendwann einmal aufgrund eines zu großen Rauschwertes eine Fehlentscheidung getroffen,  so wird die Verfälschungswahrscheinlichkeit der nachfolgenden Symbole signifikant erhöht.  Allerdings gibt es in jeder Folge immer wieder Symbolkombinationen,  die diese  "Fehlerfortpflanzung"  unterbrechen.

• Der letzte Lösungsvorschlag ist falsch.  Es gilt vielmehr:  Kleine Abstände von der Entscheiderschwelle werden vergrößert,  große Abstände dagegen verkleinert und deren Verfälschungswahrscheinlichkeiten demzufolge vergrößert.  Im Mittel führt dies aber zu einer kleineren Fehlerwahrscheinlichkeit.