Aufgabe 3.6Z: Optimaler Nyquistentzerrer für Exponentialimpuls
Aus LNTwww
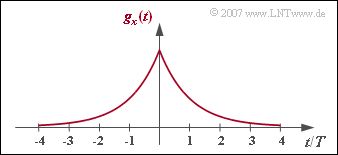
Wie in der Aufgabe 3.6 betrachten wir wieder den optimalen Nyquistentzerrer, wobei nun als Eingangsimpuls $g_x(t)$ eine beidseitig abfallende Exponentialfunktion anliegt:
- $$g_x(t) = {\rm e }^{ - |t|/T}\hspace{0.05cm}.$$
- Durch ein Transversalfilter $N$–ter Ordnung mit der Impulsantwort
- $$h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T)$$
- ist es immer möglich, dass der Ausgangsimpuls $g_y(t)$ Nulldurchgänge bei $t/T = ±1, \ \text{...} \ , \ t/T = ±N$ aufweist und $g_y(t = 0) = 1$ ist.
- Im allgemeinen Fall führen dann allerdings die Vorläufer und Nachläufer mit $| \nu | > N$ zu Impulsinterferenzen.
Hinweis: Die Aufgabe gehört zum Kapitel "Linare Nyquistentzerrung".
Fragebogen
Musterlösung
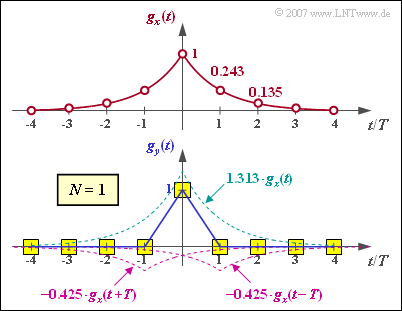
(1) Die fünf ersten Abtastwerte des Eingangsimpulses im Abstand $T$ lauten:
- $$g_x(0)\hspace{0.25cm}\underline{ = 1},\hspace{0.2cm}g_x(1) \hspace{0.25cm}\underline{= 0.368},\hspace{0.25cm}g_x(2) \hspace{0.25cm}\underline{= 0.135},\hspace{0.2cm}g_x(3) = 0.050,\hspace{0.2cm}g_x(4) {= 0.018} \hspace{0.05cm}.$$
(2) Entsprechend der Aufgabe 3.6 kommt man auf folgendes Gleichungssystem:
- $$2t = T \hspace{-0.1cm}:\hspace{0.2cm}g_1 \hspace{-0.2cm} \ = \ \hspace{-0.2cm} k_0 \cdot g_x(1) +k_1 \cdot [g_x(0)+g_x(2)]= 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{k_1}{k_0} = - \frac{g_x(1)}{g_x(0)+g_x(2)} \hspace{0.05cm},$$
- $$t = 0 \hspace{-0.1cm}:\hspace{0.2cm}g_0 \hspace{-0.2cm} \ = \ \hspace{-0.2cm} k_0 \cdot g_x(0) + k_1 \cdot 2 \cdot g_x(1) = 1\hspace{0.3cm}\Rightarrow \hspace{0.3cm} k_1 = \frac{1-k_0}{0.736} \hspace{0.05cm}.$$
- Dies führt zum Ergebnis:
- $$k_0 - 0.324 \cdot 0.736 \cdot k_0 = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} k_0 \hspace{0.15cm}\underline {= 1.313}, \hspace{0.2cm}k_1\hspace{0.15cm}\underline { = -0.425} \hspace{0.05cm}.$$
(3) Für den Zeitpunkt $t = 2T$ gilt:
- $$g_2 \ = \ k_0 \cdot g_x(2) +k_1 \cdot [g_x(1)+g_x(3)]$$
- $$\Rightarrow\hspace{0.3cm} g_2 \ = \ 1.313 \cdot 0.050 -0.425 \cdot [0.135+0.018]\hspace{0.15cm}\underline {\approx 0} \hspace{0.05cm}.$$
- Ebenso ist auch der Ausgangsimpuls zum Zeitpunkt $t = 3T$ gleich Null:
- $$g_3 \ = \ k_0 \cdot g_x(3) +k_1 \cdot [g_x(2)+g_x(4)$$
- $$\Rightarrow\hspace{0.3cm}g_3 \ = \ 1.313 \cdot 0.135 -0.425 \cdot [0.368+0.050]\hspace{0.15cm}\underline {\approx 0} \hspace{0.05cm}.$$
- Die Abbildung zeigt, dass bei diesem exponentiell abfallenden Impuls das Transversalfilter erster Ordnung eine vollständige Entzerrung bewirkt.
- Außerhalb des Intervalls $-T < t < T$ ist $g_y(t)$ identisch Null, innerhalb ergibt sich eine Dreieckform.
(4) Richtig ist nur der erste Lösungsvorschlag:
- Nachdem bereits mit einem Laufzeitfilter erster Ordnung alle Vor– und Nachläufer kompensiert werden, ergeben sich auch mit einem Filter zweiter Ordnung und auch für $N → ∞$ keine weiteren Verbesserungen.
- Dieses Ergebnis gilt jedoch ausschließlich für den (beidseitig) exponentiell abfallenden Eingansgimpuls.
- Bei fast jeder anderen Impulsform ist das Ergebnis um so besser, je größer $N$ ist.