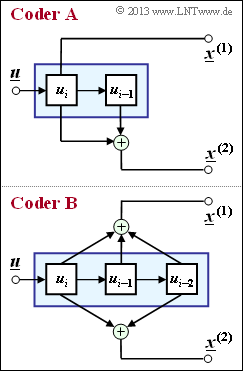
Aufgabe 3.1Z: Faltungscodes der Rate 1/2

• Zurück zum Buch

Zwei Faltungscodes der Rate  $1/2$

Die Grafik zeigt zwei Faltungscodierer der Rate  $R = 1/2$. 

• Am Eingang liegt die Informationssequenz  $\underline {u} = (u_1, u_2, \ \text{...} \ , u_i, \ \text{...})$  an.

• Hieraus werden durch Modulo–2–Operationen die beiden Sequenzen erzeugt:

$$\underline{\it x}^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( \hspace{0.05cm}x_1^{(1)}\hspace{0.05cm},\hspace{0.05cm} x_2^{(1)}\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm},\hspace{0.05cm} x_i^{(1)} \hspace{0.05cm},\text{...} \hspace{0.05cm} \big )\hspace{0.05cm},$$

$$\underline{\it x}^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( \hspace{0.05cm}x_1^{(2)}\hspace{0.05cm},\hspace{0.05cm} x_2^{(2)}\hspace{0.05cm},\hspace{0.05cm}\text{...} \hspace{0.05cm},\hspace{0.05cm} x_i^{(2)} \hspace{0.05cm}, \text{...} \hspace{0.05cm} \big ).$$

Die Sequenzen  $x_i^{(j)}$  mit  $j = 1$  bzw.  $j = 2$  können außer von  $u_i$  auch von früheren Info–Bits  $u_{i-1}, \ \text{...} \ , u_{i-m}$  abhängen. 

• Man bezeichnet  $m$  als das Gedächtnis und  $\nu = m + 1$  als die Einflusslänge des Codes bzw. des Codierers.

• Die betrachteten Coder  $\rm A$  und  $\rm B$  unterscheiden sich hinsichtlich dieser Größen.

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel  "Grundlagen der Faltungscodierung".

• In der Grafik nicht dargestellt ist das Multiplexen der beiden Teilsequenzen  $\underline {x}^{(1)}$  und  $\underline {x}^{(2)}$  zur resultierenden Codesequenz 

$$\underline {x} = (x_1^{(1)}, x_1^{(2)}, x_2^{(1)}, x_2^{(2)}, \ \text{...}).$$

• In den Teilaufgaben  (3)  bis  (5)  sollen Sie den jeweiligen Beginn der Sequenze  $\underline {x}^{(1)}, \underline{x}^{(2)}$  und  $\underline{x}$  ermitteln,  wobei von der Informationssequenz  $\underline{u} = (1, 0, 1, 1, 0, 0, \ \text{...})$  auszugehen ist.

Fragebogen

1

In welchen Codeparametern unterscheiden sich Coder  $\rm A$  und Coder  $\rm B$?

	$k$:     Anzahl der pro Codierschritt verarbeiteten Informationsbits,
	$n$:     Anzahl der pro Codierschritt ausgegebenen Codebits,
	$m$:   Gedächtnisordnung des Codes bzw. des Coders,
	$\nu$:     Einflusslänge des Codes.

2

Welcher Coder weist das Gedächtnis  $m = 2$  auf?

	Coder  $\rm A$,
	Coder  $\rm B$.

3

Wie lautet die Teilcodesequenz  $\underline {x}^{(1)}$  von Coder  $\rm B$  für  $\underline {u} = (1, 0, 1, 1, 0, 0, \ \text{...})$?

	$\underline {x}^{(1)} = (1, 1, 0, 0, 0, 1, 0, 0, \ ...)$,
	$\underline {x}^{(1)} = (1, 0, 1, 1, 0, 0, 0, 0, \ ...)$.

4

Wie lautet die Teilcodesequenz  $\underline{x}^{(2)}$  von Coder  $\rm B$  für  $\underline {u} = (1, 0, 1, 1, 0, 0, \ \text{...})$

	$\underline{x}^{(2)} = (1, 1, 0, 0, 0, 1, 0, 0, \ \text{...})$,
	$\underline{x}^{(2)} = (1, 0, 0, 1, 1, 1, 0, 0, \ \text{...})$.

5

Wie beginnt die gesamte Codesequenz  $\underline {x}$  von von Coder  $\rm B$  nach Multiplexing?

	$\underline {x} = (1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, \ \text{...})$,
	$\underline {x} = (1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, \ \text{...})$.

Musterlösung

Musterlösung

(1)  Für beide Coder gilt  $k = 1$  und  $n = 2$.

• Das Gedächtnis  $m$  und die Einflusslänge  $\nu$  sind unterschiedlich   ⇒   Antworten 3 und 4.

(2)  Das Schieberegister von Coder  $\rm A$  beinhaltet zwar zwei Speicherzellen.

Da aber   $x_i^{(1)} = u_i$ ist   und   $x_i^{(2)} = u_i + u_{i-1}$   außer vom aktuellen Informationsbit  $u_i$  nur noch vom unmittelbar vorherigen Bit  $u_{i-1}$  beeinflusst wird,  ist

Äquivalente Coder–Darstellungen

• das Gedächtnis  $m = 1$,  und

• die Einflusslänge $\nu = m + 1 = 2$.

Die Grafik zeigt die beiden Coder in anderer Darstellung,  wobei die „Gedächtnis–Speicherzellen” gelb hinterlegt sind.

• Beim Coder  $\rm A$  gibt es nur einen solchen Speicher   ⇒   $m = 1$.

• Dagegen gilt für den Coder  $\rm B$  tatsächlich  $m = 2$  und  $\nu = 3$.  Richtig ist demnach der Lösungsvorschlag 2.

(3)  Für den oberen Ausgang von Coder  $\rm B$  gilt allgemein:

$$x_i^{(1)} = u_{i} + u_{i-1}+ u_{i-2} \hspace{0.05cm}.$$

• Unter Berücksichtigung der Vorbelegung  $(u_0 = u_{-1} = 0)$  erhält man mit den obigen Angaben:

$$x_1^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{1} + u_{0}+ u_{-1} = 1+0+0 = 1 \hspace{0.05cm},\hspace{1cm}x_2^{(1)} = u_{2} + u_{1}+ u_{0} = 0+1+0 = 1\hspace{0.05cm},$$

$$x_3^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{3} + u_{2}+ u_{1} \hspace{0.25cm}= 1+0+1 = 0 \hspace{0.05cm},\hspace{1cm}x_4^{(1)} = u_{4} + u_{3}+ u_{2} = 1+1+0 = 0\hspace{0.05cm},$$

$$x_5^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{5} + u_{4}+ u_{3} \hspace{0.25cm}= 0+1+1 = 0 \hspace{0.05cm},\hspace{1cm}x_6^{(1)} = u_{6} + u_{5}+ u_{4} = 0+0+1 = 1\hspace{0.05cm},$$

$$x_7^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} x_8^{(1)} = \text{...} \hspace{0.05cm}= 0 \hspace{0.05cm}.$$

• Richtig ist somit der  Lösungsvorschlag 1.

• Der zweite Lösungsvorschlag   ⇒   $\underline {x}^{(1)} = \underline {u}$  würde dagegen nur bei einem systematischen Code gelten (der hier nicht vorliegt).

(4)  Analog zur Teilaufgabe  (3)  erhält man mit  $x_i^{(2)} = u_i + u_{i–2}$:

$$x_1^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1+0 = 1 \hspace{0.05cm},\hspace{0.2cm}x_2^{(2)} = 0+0 = 0\hspace{0.05cm}, \hspace{0.2cm}x_3^{(3)} = 1+1 = 0\hspace{0.05cm},\hspace{0.2cm}x_4^{(2)} = 1+0 = 1 \hspace{0.05cm},$$

$$x_5^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0+1 = 1\hspace{0.05cm}, \hspace{0.2cm}x_6^{(2)} = 0+1 = 1\hspace{0.05cm},\hspace{0.2cm} x_7^{(2)} = x_8^{(2)} = \text{...} \hspace{0.05cm}= 0 \hspace{0.05cm}.$$

• Richtig ist demnach der  Lösungsvorschlag 2.

(5)  Für die  (gesamte)  Codesequenz kann man formal schreiben:

$$\underline{\it x} = \big( \hspace{0.05cm}\underline{\it x}_1\hspace{0.05cm}, \hspace{0.05cm} \underline{\it x}_2\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.05cm} \underline{\it x}_i \hspace{0.05cm}, \text{...} \hspace{0.05cm} \big )\hspace{0.05cm}, \hspace{0.3cm} \underline{\it x}_i = \big( x_i^{(1)}\hspace{0.05cm}, x_i^{(2)} \big) \hspace{0.4cm}\Rightarrow \hspace{0.4cm} \underline{\it x} = \big( \hspace{0.05cm}x_1^{(1)}\hspace{0.01cm},\hspace{0.05cm} x_2^{(1)}\hspace{0.01cm},\hspace{0.05cm} x_1^{(2)}\hspace{0.01cm},\hspace{0.05cm} x_2^{(2)}\hspace{0.01cm}, \hspace{0.05cm} \text{...} \hspace{0.05cm} \big )\hspace{0.05cm}.$$

• Ein Vergleich mit den Lösungen der Aufgaben  (3)  und  (4)  zeigt die Richtigkeit von  Lösungsvorschlag 1.