Aufgabe 1.2: Bitfehlerquote (BER)
Von einem digitalen Übertragungssystem ist bekannt, dass es durch ein BSC–Modell ("Binary Symmetrical Channel") mit Fehlerwahrscheinlichkeit $p$ angenähert werden kann.
Zur Verifizierung soll die Bitfehlerquote ermittelt werden, indem man die Sinkensymbolfolge $ \langle v_\nu \rangle $ mit der Quellensymbolfolge $ \langle q_\nu \rangle $ vergleicht und daraus die Fehlerfolge $ \langle e_\nu \rangle $ ermittelt. Dabei gilt:
- $$e_\nu = \left\{ \begin{array}{c} 0 \\ 1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} v_\nu = q_\nu \hspace{0.05cm}, \\ v_\nu \ne q_\nu . \\ \end{array}$$
Die Bitfehlerquote (englisch: "Bit Error Rate") ist eine Näherung für die Bitfehlerwahrscheinlichkeit $p$ :
- $${\rm BER} = \frac{1}{N}\cdot\sum_{\nu=1}^N e_\nu.$$
Je größer der Simulationsparameter $N$ gewählt wird, um so genauer ist diese Näherung.
Aus der Aufgabe 3.7 im Buch „Stochastische Signaltheorie” ist bekannt, dass die Zufallsgröße „BER” eigentlich binominalverteilt ist, aber mit guter Näherung durch eine (diskrete) Gaußverteilung mit Mittelwert $p$ und Streuung $\sigma$ angenähert werden kann:
- $$\sigma = \sqrt{\frac{ p\cdot (\rm 1- \it p)}{N}}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel "Fehlerwahrscheinlichkeit bei Basisbandübertragung".
- Bezug genommen wird auch auf das Kapitel "Gaußverteilte Zufallsgrößen" im Buch „Stochastische Signaltheorie”.
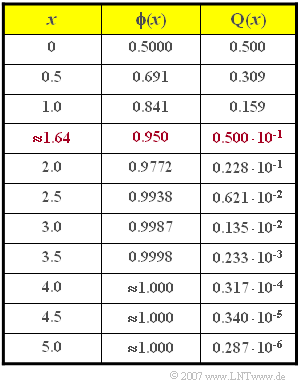
- In der Tabelle sind einige Werte der Gaußschen Fehlerfunktionen ${\rm \phi}(x)$ und ${\rm Q}(x)$ angegeben.
Fragebogen
Musterlösung
- $\rm BER$ ist der Quotient aus der Anzahl $n_{\rm B}$ der festgestellten Bitfehler und der Anzahl $N$ aller simulierten Symbole und damit tatsächlich eine relative Häufigkeit.
- Die Wahrscheinlichkeit, dass ${\rm BER} = p$ gilt, ist stets genau Null, da $\rm BER$ eine kontinuierliche Zufallsgröße darstellt.
- Allerdings wird die Wahrscheinlichkeit, dass $\rm BER$ in einem schmalen Intervall um $p$ liegt, mit steigendem $N$ immer größer.
(2) Die Streuung der Gaußschen Zufallsgröße $\rm BER $ ergibt sich mit $N = 10^6$ und $p = 10^{-2}$ zu
- $$\sigma = \sqrt{{ p\cdot (\rm 1- \it p)}/{N}}\approx \sqrt{{ p}/{N}}\hspace{0.1cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$
(3) Die Wahrscheinlichkeit, dass $\rm BER$ einen Wert außerhalb des Bereichs
$0.95 \cdot p$ ... $1.05 \cdot p$ annimmt, ergibt sich mit $\varepsilon = 5 \cdot 0^{-4}$ $($wegen $p = 10^{-2})$ zu
- $${\rm Pr} \left( {\rm BER} < 0.95 \cdot 10^{-2} \right) = {\rm Pr} \left( {\rm BER} > 1.05 \cdot 10^{-2} \right) = {\rm Q} \left({\varepsilon}/{\sigma} \right)$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr} \left( |{\rm BER} - p| > \varepsilon \right) = 2 \cdot {\rm Q} \left( \frac{5 \cdot 10^{-4}}{10^{-4}} \right) = 2 \cdot 0.287 \cdot 10^{-6}\hspace{0.1cm}\underline {= 0.00574 \cdot 10^{-4}}\hspace{0.05cm}.$$
(4) Mit $p = 10^{-4}$ gilt für die vergleichbare Wahrscheinlichkeit:
- $${\rm Pr} \left( |{\rm BER} - 10^{-4}| > 0.05 \cdot 10^{-4} \right) = 2 \cdot {\rm Q} \left( {\varepsilon}/{\sigma} \right);\hspace{0.5cm} \text{mit}\hspace{0.5cm}\sigma \approx \sqrt{{ p}/{N}}= 10^{-5}\hspace{0.05cm}, \hspace{0.3cm}\varepsilon = 5 \cdot 10^{-6}\text{:}$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr} \left( |{\rm BER} - 10^{-4}| > 0.05 \cdot 10^{-4} \right) = 2 \cdot {\rm Q} \left( \frac{5 \cdot 10^{-6}}{10^{-5}} \right) = 2 \cdot 0.309 \hspace{0.1cm}\underline {= 0.618} \hspace{0.05cm}.$$
(5) Diese Bedingung lässt sich mit $\varepsilon = 5 \cdot 10^{-6}$ wie folgt formulieren:
- $${\rm Q} \left( {\varepsilon}/{\sigma} \right) < 0.1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\varepsilon}/{\sigma} > {\rm Q}^{-1}(0.05) \approx 1.64 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{\varepsilon^2}{\sigma^2}\approx \frac{\varepsilon^2 \cdot N}{p}> 1.64^2 = 2.69$$
- $$\Rightarrow \hspace{0.3cm} N > \frac{2.69 \cdot p}{\varepsilon^2}= \frac{2.69 \cdot 10^{-4}}{25 \cdot10^{-12}}\hspace{0.1cm}\underline {\approx 10.8 \cdot 10^{6}}\hspace{0.05cm}.$$