Am Eingang eines Tiefpasses mit rechteckförmiger Impulsantwort $h(t)$ liegt das Empfangssignal $r(t)$ an, das sich additiv aus einem impulsförmigen Nutzsignal $g(t)$ und einem Rauschsignal $n(t)$ zusammensetzt. Es gelte:
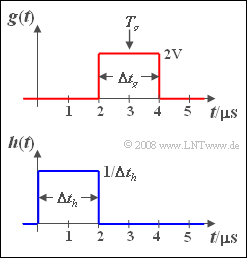
- Der Nutzimpuls $g(t)$ ist rechteckförmig.
- Die Impulsdauer beträgt $\Delta t_g = 2 \hspace{0.08cm}\rm µ s$.
- Die Impulsamplitude ist $g_0 = 2 \hspace{0.08cm}\rm V$.
- Die Mitte des Impulses liegt bei $T_g = 3 \hspace{0.08cm}\rm µ s$.
- Das Rauschen $n(t)$ ist weiß und gaußverteilt.
- Die Rauschleistungsdichte beträgt $N_0 = 4 \cdot 10^{-6} \hspace{0.08cm}\rm V^2\hspace{-0.1cm}/Hz$ bezogen auf den Widerstand $1 \hspace{0.08cm}\rm \Omega$.
Die rechteckförmige Impulsantwort des Filters beginnt bei $t = 0$.
- Die Impulsantwortdauer $\Delta t_h$ ist frei wählbar.
- Die Höhe $1/\Delta t_h$ der Impulsantwort ist jeweils so angepasst, dass $H(f = 0) = 1$ gilt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Matched-Filter.
- Für die Teilfragen (1) bis (6) gelte stets $\Delta t_h =\Delta t_g = 2 \hspace{0.05cm}\rm µ s$.
Fragebogen
Musterlösung
- Bei gleicher Impulsdauer $(\Delta t_h =\Delta t_g)$ liegt ein Matched-Filter vor, auch wenn sich $g(t)$ und $h(t)$ hinsichtlich Amplitude und zeitlicher Lage unterscheiden.
- Damit gibt es auch kein anderes Filter mit besserem Signal–zu–Rauschleistungsverhältnis.
- Das Filter mit rechteckförmiger Impulsantwort lässt sich auch als ein Integrator über die Zeitdauer $\Delta t_h$ interpretieren.
(2) Die Impulsantwort des Matched–Filters lautet: $h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$
- Der Eingangsimpuls $g(t)$ ist im Bereich von $2 \hspace{0.05cm}\rm µ s$ bis $4 \hspace{0.08cm}\rm µ s$ ungleich Null, bei Spiegelung im Bereich von $-4 \hspace{0.08cm}\rm µ s$ bis $-2 \hspace{0.08cm}\rm µ s$.
- Durch eine Verschiebung um $4 \hspace{0.08cm}\rm µ s$ wird erreicht, dass $g(T_{\rm D} - t)$ wie die Impulsantwort $h(t)$ zwischen $0$ und $2 \hspace{0.08cm}\rm µ s$ liegt. Daraus folgt: $T_\text{D, opt}\hspace{0.15cm}\underline{ =4 \hspace{0.08cm}\rm µ s}$.
(3) Mit $\Delta t_h =\Delta t_g = 2 \cdot 10^{-6}\hspace{0.05cm}\rm µ s$ und $g_0 = 2 \hspace{0.08cm}\rm V$ erhält man $K_{\rm MF} 1/(\Delta t_g \cdot g_0)\hspace{0.15cm}\underline{ =0.25 \cdot 10^{6}\hspace{0.08cm}\rm (1/Vs)}$.
(4) Die Energie des Nutzimpulses $g(t)$ ist $E_g = g_0^2 \cdot \Delta t_g = 8 \cdot 10^{-6}\hspace{0.05cm}\rm V^2s$.
- Daraus folgt für das maximale S/N–Verhältnis:
- $$\rho _d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) = \frac{2 \cdot E_g }{N_0 } = \frac{{2 \cdot 8 \cdot 10^{ - 6} \;{\rm{V}}^2 {\rm{s}}}}{{4 \cdot 10^{ - 6} \;{\rm{V}}^2 /{\rm{Hz}}}}\hspace{0.15cm}\underline{ = 4}.$$
(5) Der Ausgangsimpuls $d_{\rm S}(t)$ ist dreieckförmig zwischen $2 \hspace{0.05cm}\rm µ s$ und $6 \hspace{0.05cm}\rm µ s$.
- Das Maximum $g_0\hspace{0.15cm}\underline{= 2 \hspace{0.08cm}\rm V}$ liegt bei $T_\text{D, opt} =4 \hspace{0.05cm}\rm µ s$.
- Die Störleistung ergibt sich zu:
- $$\sigma _d ^2 = \frac{N_0 }{2 \cdot \Delta t_h } \hspace{0.15 cm}\underline{= 1\;{\rm{V}}^2} .$$
- Mit diesen beiden Rechengrößen kann man wiederum das maximale S/N-Verhältnis berechnen:
- $$\rho _d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) = \frac{{d_{\rm S} (T_{{\rm{D, \hspace{0.05cm}opt}}} )^2}}{\sigma _d ^2 } = \frac{({2\;{\rm{V}})^2 }}{{1\;{\rm{V}}^2 }} = 4.$$
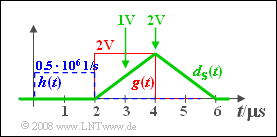
(6) Aus obiger Skizze erkennt man, dass nun der Nutzabtastwert nur mehr halb so groß ist, nämlich $1 \hspace{0.08cm}\rm V$.
- Damit ist für $T_\text{D, opt} =3 \hspace{0.08cm}\rm µ s$ das S/N–Verhältnis um den Faktor $4$ kleiner, also $\rho _d (T_{{\rm{D, \hspace{0.08cm}opt}}} )\hspace{0.15 cm}\underline{=1}$.
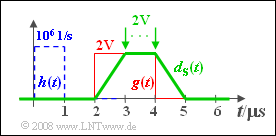
(7) Richtig sind die Lösungsvorschläge 1, 3 und 4:
- Die Skizze zeigt, dass nun der Ausgangsimpuls $d_{\rm S}(t)$ trapezförmig verläuft.
- Im Bereich von $3 \hspace{0.05cm}\rm µ s$ bis $4 \hspace{0.05cm}\rm µ s$ ist der Nutzabtastwert konstant gleich $g_0= 2 \hspace{0.08cm}\rm V$
- Wegen der nur halb so breiten Impulsantwort $h(t)$ ist der Frequenzgang $H(f)$ um den Faktor $2$ breitbandiger. Dadurch ist die Störleistung größer:
- $$\sigma_d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {h^2 (t)\,{\rm{d}}t} = \frac{N_0 }{2 \cdot \Delta t_h } = 2\;{\rm{V}}^2 .$$
- Damit ergibt sich für das S/N–Verhältnis nun der Wert $\rho_d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) \hspace{0.15cm}\underline{= 2}.$
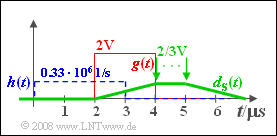
(8) Richtig sind hier die Lösungsvorschläge 2 und 4:
- Rechts ist der Ausgangsimpuls $d_{\rm S}(t)$ für $\Delta t_h = 3 \hspace{0.05cm}\rm µ s$ skizziert. Auch dieser ist trapezförmig.
- Der optimale Detektionszeitpunkt liegt nun im Bereich zwischen $4 \hspace{0.05cm}\rm µ s$ und $5 \hspace{0.05cm}\rm µ s$.
- Das Nutzsignal ist aber nun nur mehr ein Drittel so groß als bei Anpassung: $d_{\rm S}(T_\text{D, opt}) = 2/3 \hspace{0.08cm}\rm V$.
- Für die Störleistung gilt nun:
- $$\sigma_d ^2 = \frac{N_0 }{2 \cdot \Delta t_h } = \frac{2}{3}\;{\rm{V}}^2 .$$
- Die Störleistung ist somit zwar kleiner (also günstiger) als bei Anpassung entsprechend der Teilaufgabe (5).
- Trotzdem ist das S/N–Verhältnis aufgrund des kleineren Nutzabtastwertes noch schlechter als in Teilaufgabe (7):
- $$\rho _d (T_{{\rm{D\hspace{0.05cm},opt}}} ) = \frac{{(2/3\;{\rm{V}})^2 }}{{2/3\;{\rm{V}}^2 }} = {2}/{3}.$$