Aufgabe 4.3Z: Exponential– und Laplaceverteilung
Wir betrachten hier die Wahrscheinlichkeitsdichtefunktionen $\rm (WDF)$ zweier wertkontinuierlicher Zufallsgrößen:
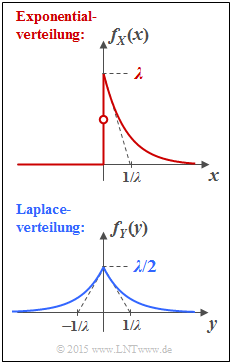
- Die Zufallsgröße $X$ ist exponentialverteilt (siehe obere Darstellung): Für $x<0$ ist $f_X(x) = 0$, und für positive $x$–Werte gilt:
- $$f_X(x) = \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.05cm}. $$
- Dagegen gilt für die laplaceverteilte Zufallsgröße $Y$ im gesamten Bereich $ - \infty < y < + \infty$ (untere Skizze):
- $$f_Y(y) = \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|\hspace{0.05cm}y\hspace{0.05cm}|}\hspace{0.05cm}.$$
Zu berechnen sind die differentiellen Entropien $h(X)$ und $h(Y)$ abhängig vom WDF–Parameter $\it \lambda$. Zum Beispiel gilt:
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [f_X(x) \big ] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Bei Verwendung von $\log_2$ ist die Pseudo–Einheit „bit” anzufügen.
In den Teilaufgaben (2) und (4) ist die differentielle Entropie in folgender Form anzugeben:
- $$h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(X)} \cdot \sigma^2) \hspace{0.5cm}{\rm bzw.} \hspace{0.5cm}h(Y) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(Y)} \cdot \sigma^2) \hspace{0.05cm}.$$
Zu ermitteln ist, durch welchen Faktor ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(X)}$ die Exponentialverteilung charakterisiert wird und welcher Faktor ${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(Y)}$ sich für die Laplaceverteilung ergibt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Differentielle Entropie.
- Nützliche Hinweise zur Lösung dieser Aufgabe finden Sie insbesondere auf der Seite Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen.
- Für die Varianz der exponentialverteiten Zufallsgröße $X$ gilt, wie in Aufgabe 4.1Z hergeleitet: $\sigma^2 = 1/\lambda^2$.
- Die Varianz der laplaceverteiten Zufallsgröße $Y$ ist bei gleichem $\it \lambda$ doppelt so groß: $\sigma^2 = 2/\lambda^2$.
Fragebogen
Musterlösung
- Dann gilt für die differentielle Entropie:
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} \big [f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
- Für die Exponentialverteilung sind die Integrationsgrenzen $0$ und $+∞$ anzusetzen. In diesem Bereich wird die WDF $f_X(x)$ gemäß Angabenblatt eingesetzt:
- $$h(X) =- \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} \hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda) + {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x})\right ]\hspace{0.1cm}{\rm d}x - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x \hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Man erkennt:
- Der erste Integrand ist identisch mit der hier betrachteten WDF $f_X(x)$. Das Integral über den gesamten Integrationsbereich ergibt somit $1$.
- Das zweite Integral entspricht genau der Definition des Mittelwertes $m_1$ (Moment erster Ordnung). Für die Exponentialverteilung gilt $m_1 = 1/λ$. Daraus folgt:
- $$h(X) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + 1 = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} ({\rm e}/\lambda) \hspace{0.05cm}.$$
- Dieses Ergebnis ist mit der Zusatzeinheit „nat” zu versehen. Mit $\log_2$ anstelle von $\ln$ erhält man die differentielle Entropie in „bit”:
- $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} \hspace{0.3cm} h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}) = \frac{{\rm ln} \hspace{0.1cm} ({\rm e})}{{\rm ln} \hspace{0.1cm} (2)} \hspace{0.15cm}\underline{= 1.443\,{\rm bit}} \hspace{0.05cm}.$$
(2) Unter Berücksichtigung der für die Exponentialverteilung gültigen Gleichung $\sigma^2 = 1/\lambda^2$ kann man das in (1) gefundene Ergebnis wie folgt umformen:
- $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) = {1}/{2}\cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2/\lambda^2) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2 \cdot \sigma^2) \hspace{0.05cm}.$$
- Ein Vergleich mit der geforderten Grundform $h(X) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L}^{\hspace{0.08cm}(X)} \cdot \sigma^2)$ führt zum Ergebnis:
- $${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(X)} = {\rm e}^2 \hspace{0.15cm}\underline{\approx 7.39} \hspace{0.05cm}.$$
(3) Bei der Laplaceverteilung unterteilen wir den Integrationsbereich in zwei Teilbereiche:
- $Y$ negativ ⇒ Anteil $h_{\rm neg}(Y)$,
- $Y$ positiv ⇒ Anteil $h_{\rm pos}(Y)$.
Die gesamte differentielle Entropie ergibt sich unter Berücksichtigung von $h_{\rm neg}(Y) = h_{\rm pos}(Y)$ zu
- $$h(Y) = h_{\rm neg}(Y) + h_{\rm pos}(Y) = 2 \cdot h_{\rm pos}(Y) $$
- $$\Rightarrow \hspace{0.3cm} h(Y) = - 2 \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y} \hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda/2) + {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y})\right ]\hspace{0.1cm}{\rm d}y = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y \hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot y \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$
Berücksichtigen wir wiederum, dass das erste Integral den Wert $1$ ergibt (WDF–Fläche) und das zweite Integral den Mittelwert $m_1 = 1/\lambda$ angibt, so erhalten wir:
- $$h(Y) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + 1 = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (2{\rm e}/\lambda) \hspace{0.05cm}.$$
- Da das Ergebnis in „bit” gefordert ist, muss noch $\ln$ durch $\log_2$ ersetzt werden:
- $$h(Y) = {\rm log}_2 \hspace{0.1cm} (2{\rm e}/\lambda) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} \hspace{0.3cm} h(Y) = {\rm log}_2 \hspace{0.1cm} (2{\rm e}) \hspace{0.15cm}\underline{= 2.443\,{\rm bit}} \hspace{0.05cm}.$$
(4) Bei der Laplaceverteilung gilt der Zusammenhang $\sigma^2 = 2/\lambda^2$. Damit erhält man:
- $$h(X) = {\rm log}_2 \hspace{0.1cm} (\frac{2{\rm e}}{\lambda}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (\frac{4{\rm e}^2}{\lambda^2}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (2 {\rm e}^2 \cdot \sigma^2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(Y)} = 2 \cdot {\rm e}^2 \hspace{0.15cm}\underline{\approx 14.78} \hspace{0.05cm}.$$
- Der ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}$–Wert ist demzufolge bei der Laplaceverteilung doppelt so groß wie bei der Exponentialverteilung.
- Die Laplaceverteilung ist also bezüglich der differentiellen Entropie besser als die Exponentialverteilung, wenn man von leistungsbegrenzten Signalen ausgeht.
- Unter der Nebenbedingung der Spitzenwertbegrenzung sind sowohl die Exponential– als auch die Laplaceverteilung völlig ungeeignet, ebenso wie die Gaußverteilung. Diese reichen alle bis ins Unendliche.