Aufgabe 4.18: Nichtkohärente FSK–Demodulation
Wir betrachten "Frequency Shift Keying" $\rm (FSK)$ mit $M = 2$ ⇒ binäre Signalisierung. Die beiden Basisfunktionen im Tiefpassbereich sind in diesem Fall komplex und lauten:
- $$\xi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$
- $$ \xi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}.$$
Für die zwei möglichen Signalformen im Tiefpassbereich gilt dann mit der mittleren Symbolenergie $E_{\rm S}$:
- $$m_0\text{:}\hspace{0.2cm} s_{\rm TP,\hspace{0.05cm}0} = \sqrt{E_{\rm S}} \cdot \xi_1(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\boldsymbol{ s}_{\rm 0} = (\sqrt{E_{\rm S}}, 0)\hspace{0.05cm},$$
- $$m_1\text{:}\hspace{0.2cm} s_{\rm TP,\hspace{0.05cm}1} = \sqrt{E_{\rm S}} \cdot \xi_2(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\boldsymbol{ s}_{\rm 1} = (0, \sqrt{E_{\rm S}})\hspace{0.05cm}.$$
Hierbei gibt $h$ den so genannten "Modulationsindex" an. Dieser muss gewisse Kriterien erfüllen, damit sich orthogonale Signalformen ergeben. Diese Kriterien hängen allerdings davon ab, ob beim Empfänger ein kohärenter oder ein nichtkohärenter Demodulator verwendet wird.
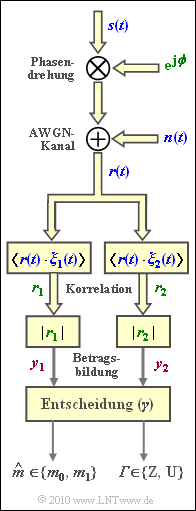
Die Grafik zeigt im unteren Bereich den nichtkohärenten Demodulator für binäres "Frequency Shift Keying" $\rm (BFSK)$. Alle komplexen Signale sind blau beschriftet, komplexe Werte grün und reelle Werte rot.
Gegenüber dem im "Theorieteil" angegeben Entscheidungsprozess wird nun ein komplizierter Entscheider betrachtet, der außer dem Schätzwert noch ein "Sicherheitsflag" ${\it \Gamma} = \{{\rm Z}, \ {\rm U}\}$ ausgibt. Die logischen Größen stehen hierbei für
- ${\rm Z}$ ⇒ Zuverlässige Entschedung,
- ${\rm U}$ ⇒ Unzuverlässige Entschedung.
Es gibt also vier Möglichkeiten der Entscheidung, gesteuert durch den Parameter $\gamma$:
- $$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_0,\hspace{0.15cm}{\it \Gamma} = {\rm Z}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_1 > \gamma \cdot y_2\hspace{0.05cm},$$
- $$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_0,\hspace{0.15cm}{\it \Gamma} = {\rm U}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_2 < y_1 < \gamma \cdot y_2\hspace{0.05cm},$$
- $$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_1,\hspace{0.15cm}{\it \Gamma} = {\rm Z}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_2 > \gamma \cdot y_1\hspace{0.05cm},$$
- $$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_1,\hspace{0.15cm}{\it \Gamma} = {\rm U}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_1 < y_2 < \gamma \cdot y_1\hspace{0.05cm}.$$
In den Fragen zur Aufgabe werden die beiden Werte $\gamma = 1$ und $\gamma = 2$ betrachtet.
Für die Wahrscheinlichkeit, dass sich der Entscheider fälschlicherweise für das Symbol $m_1$ entscheidet und zudem anzeigt, dass diese Entscheidung als zuverlässig zu betrachten ist (das ist besonders verwerflich), gilt
- $${\rm Pr}\{\hat{m} = m_1,\hspace{0.05cm}{\it \Gamma} = {\rm Z} \hspace{0.05cm}| \hspace{0.05cm}m_0 \} = \frac{1}{1 + \gamma^2} \cdot {\rm exp } \left [ - \frac{\gamma^2 \cdot E_{\rm S}}{(1+\gamma^2) \cdot N_{\rm 0}}\right ] \hspace{0.05cm}.$$
Hinweis: Die Aufgabe gehört zum Kapitel "Trägerfrequenzsysteme mit nichtkohärenter Demodulation".
Fragebogen
Musterlösung
- Bei kohärenter Demodulation ist Orthogonalität dann gegeben, wenn der Modulationsindex $h$ ein Vielfaches von $0.5$ ist. Binäre FSK mit $h = 0.5$ nennt man auch "Minimum Shift Keying" $\rm (MSK)$.
- Da durch die Phasenregelung die Phasenverschiebung ("Laufzeit") auf dem AWGN–Übertragungskanal ausgeglichen wird ⇒ ${\rm e}^{{\rm j}\phi} \cdot {\rm e}^{-{\rm j}\phi} = 1$, gilt tatsächlich für die Signale im äquivalenten Tiefpassbereich: $r(t) = s(t) + n(t) \hspace{0.05cm}.$
(2) Hier ist nur der erste Lösungsvorschlag richtig, das heißt, es muss nun $h = 1, \ 2, \ 3, \text{ ...}$ ganzzahlig sein.
- Nichtkohärente Demodulation von BFSK ist somit nicht möglich.
- Wegen der fehlenden Phasenregelung gilt außerdem:
- $$r(t) = s(t) \cdot {\rm e }^{ - {\rm j }\hspace{0.05cm}\phi} + n(t) \hspace{0.05cm}.$$
(3) Bei gleichwahrscheinlichen Nachrichten gilt:
- $$p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Pr}({\cal{E}}| \hspace{0.05cm}m = m_0) = {\rm Pr}(\hat{m}= m_1| \hspace{0.05cm}m = m_0)\hspace{0.05cm}.$$
- Diese Wahrscheinlichkeit ergibt sich aus der vorgegebenen Gleichung mit $\gamma = 1$.
- In diesem Fall ist stets ${\it \Gamma} ={\rm Z}$ und die Entscheidungsregel lautet: "Entscheide auf das Symbol $m_0$, falls $y_1 > y_2$".
- Daraus folgt:
- $$p_{\rm S} = \frac{1}{1 + \gamma^2} \cdot {\rm exp } \left [ - \frac{\gamma^2 \cdot E_{\rm S}}{(1+\gamma^2) \cdot N_{\rm 0}}\right ]_{\gamma = 1} = {1}/{2} \cdot {\rm e }^{-E_{\rm S}/(2N_0)}\hspace{0.05cm}.$$
- Mit $E_{\rm S}/N_0 = 10$ erhält man $p_{\rm S} = 1/2 \cdot {\rm e}^{\rm –5} \approx \underline {0.337 \cdot \%}$.
(4) Diese Wahrscheinlichkeit ergibt sich aus Symmetriegründen zu
- $${\rm Pr}({\it \Gamma} = {\rm Z}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm Fehler} ) = {1}/{2} \cdot {\rm Pr}\{(\hat{m} = m_1)\hspace{0.05cm}\cap\hspace{0.05cm}{\it \Gamma} = {\rm Z} \hspace{0.05cm}| \hspace{0.05cm}m_0 \} + {1}/{2}\cdot {\rm Pr}\{(\hat{m} = m_0)\hspace{0.05cm}\cap\hspace{0.05cm}({\it \Gamma} = {\rm Z}) \hspace{0.05cm}| \hspace{0.05cm}m_1 \} $$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr}({\it \Gamma} = {\rm Z}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm Fehler} ) = {\rm Pr}\{(\hat{m} = m_1)\hspace{0.05cm}\cap\hspace{0.05cm}({\it \Gamma} = {\rm Z}) \hspace{0.05cm}| \hspace{0.05cm}m_0 \} =\frac{1}{1 + 2^2} \cdot {\rm exp } \left [ - \frac{2^2 \cdot E_{\rm S}}{(1+2^2) \cdot N_{\rm 0}}\right ] = {1}/{5} \cdot {\rm e }^{-8} = \underline{6.7 \cdot 10^{-5}}\hspace{0.05cm}.$$
(5) Da ${\rm U}$ und ${\rm Z}$ nach der Statistik ein "vollständiges System" ergeben, gilt mit den Ergebnissen der Teilaufgaben (3) und (4):
- $${\rm Pr}({\it \Gamma} = {\rm U}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm Fehler} ) ={\rm Pr}( {\rm Fehler} ) - {\rm Pr}({\it \Gamma} = {\rm Z}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm Fehler} ) = 3.37 \cdot 10^{-3} - 6.7 \cdot 10^{-5} = \underline{3.3 \cdot 10^{-3}} \hspace{0.05cm}.$$
- Damit ist die gesuchte bedingte Wahrscheinlichkeit ${\rm Pr}({\it \Gamma}= {\rm U}\hspace{0.05cm}|\hspace{0.05cm} {\rm Fehler})$:
- $${\rm Pr}({\it \Gamma}= {\rm U}\hspace{0.05cm}|\hspace{0.05cm} {\rm Fehler} ) = \frac{{\rm Pr}({\it \Gamma} = {\rm U}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm Fehler} ) }{{\rm Pr}( {\rm Fehler} )} = \frac{3.3 \cdot 10^{-3}}{3.37 \cdot 10^{-3}} \hspace{0.15cm} \underline{= 98 \%} \hspace{0.05cm}.$$