Aufgaben:Aufgabe 2.08Z: „Plus” und „Mal” in GF(2 hoch 3): Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Definition und Eigenschaften von Reed–Solomon–Codes }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simpl…“) |
|||
| (22 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Kanalcodierung/Definition und Eigenschaften von Reed–Solomon–Codes | + | {{quiz-Header|Buchseite=Kanalcodierung/Definition und Eigenschaften von Reed–Solomon–Codes}} |
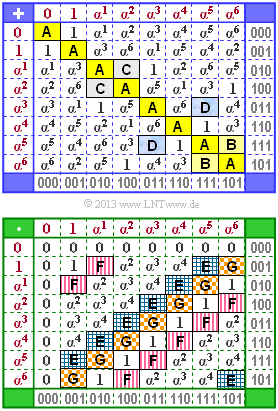
| + | [[Datei:P_ID2536__KC_Z_2_8.png|right|frame|$\rm GF(2^3)$: Unvollständige Additions– und Multiplikationstabellen]] | ||
| + | Die Grafik zeigt die Additions– und Multiplikationstabelle für den endlichen Körper $\rm GF(2^3)$. Die Tabellen sind nicht vollständig. Einige (farblich hervorgehobene) Felder sollen Sie ergänzen. | ||
| + | Die Elemente sind sowohl | ||
| + | *in der Exponentendarstellung $($mit roter Beschriftung, links und oben$)$ als auch | ||
| + | *in der Koeffizientendarstellung $($graue Schrift, rechts und unten$)$ | ||
| − | |||
| − | [[ | + | angegeben. Aus dieser Zuordnung erkennt man bereits das zugrunde liegende irreduzible Polynom $p(\alpha)$. |
| + | |||
| + | *Additionen $($und Subtraktionen$)$ führt man am besten in der Koeffizientendarstellung $($oder mit den damit fest verknüpften Polynomen$)$ durch. | ||
| + | |||
| + | *Für Multiplikationen ist dagegen die Exponentendarstellung günstiger. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Definition_und_Eigenschaften_von_Reed%E2%80%93Solomon%E2%80%93Codes| "Definition und Eigenschaften von Reed–Solomon–Codes"]]. | ||
| + | |||
| + | * Bezug genommen wird aber auch auf das Kapitel [[Kanalcodierung/Erweiterungsk%C3%B6rper| "Erweiterungskörper"]]. | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
| − | |||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Für welches Element steht das "$\rm A$" in der Additionstabelle? |
| − | |type=" | + | |type="()"} |
| − | - | + | + $\rm A = 0$, |
| − | + | - $\rm A = 1$, | |
| + | - $\rm A = \alpha^1$, | ||
| + | {Für welches Element steht das "$\rm B$" in der Additionstabelle? | ||
| + | |type="()"} | ||
| + | - $\rm B = 0$, | ||
| + | - $\rm B = 1$, | ||
| + | + $\rm B = \alpha^1$. | ||
| − | { | + | {Für welches Element steht das "$\rm C$" in der Additionstabelle? |
| − | |type=" | + | |type="()"} |
| − | $\alpha$ = | + | - $\rm C = \alpha^2$, |
| + | - $\rm C = \alpha^3$, | ||
| + | + $\rm C = \alpha^4$. | ||
| + | {Für welches Element steht das "$\rm D$" in der Additionstabelle? | ||
| + | |type="()"} | ||
| + | + $\rm D = \alpha^2$, | ||
| + | - $\rm D = \alpha^3$, | ||
| + | - $\rm D = \alpha^4$. | ||
| + | {Welche Zuordnungen gelten in der Multiplikationstabelle? | ||
| + | |type="[]"} | ||
| + | + $\rm E = \alpha^5$, | ||
| + | + $\rm F = \alpha^1$, | ||
| + | + $\rm G = \alpha^6$. | ||
| + | {Welches irreduzible Polynom liegt diesen Tabellen zugrunde? | ||
| + | |type="()"} | ||
| + | - $p(\alpha) = \alpha^2 + \alpha + 1$, | ||
| + | - $p(\alpha) = \alpha^3 + \alpha^2 + 1$, | ||
| + | + $p(\alpha) = \alpha^3 + \alpha + 1$. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Die Addition eines jeden Elements eines Erweiterungskörpers, der auf $\rm GF(2)$ basiert, mit sich selbst ergibt stets $0$, wie man anhand der Koeffizientendarstellung leicht erkennt, zum Beispiel: |
| − | '''2 | + | :$$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 |
| − | '''3 | + | \hspace{0.05cm}.$$ |
| − | '''4 | + | |
| − | '''5 | + | *Das heißt: "$\rm A$" steht für das Nullelement ⇒ <u>Lösungsvorschlag 1</u>. |
| − | + | ||
| − | + | ||
| − | {{ | + | |
| + | '''(2)''' "$\rm B$" ist das Ergebnis der Addition von $\alpha^5$ und $\alpha^6$ ⇒ <u>Lösungsvorschlag 3</u>: | ||
| + | :$$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Man hätte dieses Ergebnis auch einfacher finden können, da in jeder Zeile und Spalte jedes Element genau einmal vorkommt. | ||
| + | |||
| + | *Nachdem $\rm A = 0$ festliegt, fehlt in der letzten Zeile und der letzten Spalte genau nur noch das Element $\alpha^1$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' "$\rm C$" ist das Ergebnis der Summe von $\alpha^1$ und $\alpha^2$ ⇒ <u>Lösungsvorschlag 3</u>: | ||
| + | :$$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' "$\rm D$" ist das Ergebnis von $\alpha^3$ und $\alpha^5$ ⇒ <u>Lösungsvorschlag 1</u>: | ||
| + | :$$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' <u>Alle Lösungsvorschläge</u> sind richtig, wie man aus der Zeile 2 ("Multiplikation mit dem Einselelement") erkennt: | ||
| + | [[Datei:P_ID2573__KC_Z_2_8e.png|right|frame|$\rm GF(2^3)$: Vollständige Additions– und Multiplikationstabellen]] | ||
| + | *Nebenstehend sehen Sie die vollständigen Tabellen für die Addition und die Multiplikation. | ||
| + | |||
| + | *Aufgrund der Gültigkeit von $\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7} $ ergibt sich bei der Multiplikation eine Symmetrie, die man zur Lösung nutzen könnte. | ||
| + | |||
| + | |||
| + | '''(6)''' Richtig ist hier der <u>Lösungsvorschlag 3</u>: | ||
| + | * Alle Polynome sind zwar irreduzibel. Man benötigt aber für $\rm GF(2^3)$ ein Grad–3–Polynom. | ||
| + | *Der dritte Lösungsvorschlag ergibt sich aus der Beziehung | ||
| + | :$$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | p(\alpha) = \alpha^3 + \alpha + 1 = 0 \hspace{0.05cm}.$$ | ||
| + | {{ML-Fuß}} | ||
| − | |||
| − | ^]] | + | [[Category:Aufgaben zu Kanalcodierung|^2.3 Zu den Reed–Solomon–Codes^]] |
Aktuelle Version vom 10. Oktober 2022, 16:59 Uhr
Die Grafik zeigt die Additions– und Multiplikationstabelle für den endlichen Körper $\rm GF(2^3)$. Die Tabellen sind nicht vollständig. Einige (farblich hervorgehobene) Felder sollen Sie ergänzen.
Die Elemente sind sowohl
- in der Exponentendarstellung $($mit roter Beschriftung, links und oben$)$ als auch
- in der Koeffizientendarstellung $($graue Schrift, rechts und unten$)$
angegeben. Aus dieser Zuordnung erkennt man bereits das zugrunde liegende irreduzible Polynom $p(\alpha)$.
- Additionen $($und Subtraktionen$)$ führt man am besten in der Koeffizientendarstellung $($oder mit den damit fest verknüpften Polynomen$)$ durch.
- Für Multiplikationen ist dagegen die Exponentendarstellung günstiger.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Definition und Eigenschaften von Reed–Solomon–Codes".
- Bezug genommen wird aber auch auf das Kapitel "Erweiterungskörper".
Fragebogen
Musterlösung
- $$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 \hspace{0.05cm}.$$
- Das heißt: "$\rm A$" steht für das Nullelement ⇒ Lösungsvorschlag 1.
(2) "$\rm B$" ist das Ergebnis der Addition von $\alpha^5$ und $\alpha^6$ ⇒ Lösungsvorschlag 3:
- $$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$
- Man hätte dieses Ergebnis auch einfacher finden können, da in jeder Zeile und Spalte jedes Element genau einmal vorkommt.
- Nachdem $\rm A = 0$ festliegt, fehlt in der letzten Zeile und der letzten Spalte genau nur noch das Element $\alpha^1$.
(3) "$\rm C$" ist das Ergebnis der Summe von $\alpha^1$ und $\alpha^2$ ⇒ Lösungsvorschlag 3:
- $$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$
(4) "$\rm D$" ist das Ergebnis von $\alpha^3$ und $\alpha^5$ ⇒ Lösungsvorschlag 1:
- $$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 \hspace{0.05cm}.$$
(5) Alle Lösungsvorschläge sind richtig, wie man aus der Zeile 2 ("Multiplikation mit dem Einselelement") erkennt:
- Nebenstehend sehen Sie die vollständigen Tabellen für die Addition und die Multiplikation.
- Aufgrund der Gültigkeit von $\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7} $ ergibt sich bei der Multiplikation eine Symmetrie, die man zur Lösung nutzen könnte.
(6) Richtig ist hier der Lösungsvorschlag 3:
- Alle Polynome sind zwar irreduzibel. Man benötigt aber für $\rm GF(2^3)$ ein Grad–3–Polynom.
- Der dritte Lösungsvorschlag ergibt sich aus der Beziehung
- $$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p(\alpha) = \alpha^3 + \alpha + 1 = 0 \hspace{0.05cm}.$$