Aufgaben:Aufgabe 1.4: Nyquistkriterien: Unterschied zwischen den Versionen
| Zeile 63: | Zeile 63: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
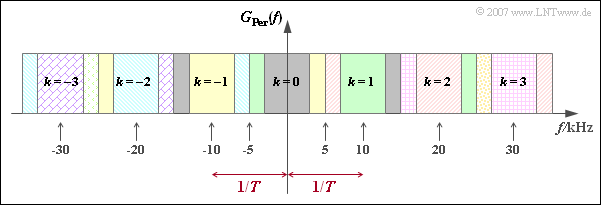
| − | '''(1)''' Die folgende Grafik zeigt das Spektrum (der Index „Per” steht hier für „Periodische Fortsetzung”): | + | '''(1)''' Die folgende Grafik zeigt das Spektrum (der Index „Per” steht hier für „Periodische Fortsetzung”): |
| + | [[Datei:P_ID1280__Dig_A_1_4a.png|right|frame|Zur Verdeutlichung des ersten Nyquistkriteriums]] | ||
| + | |||
:$$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} G(f - | :$$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} G(f - | ||
\frac{k}{T} ) \hspace{0.05cm}.$$ | \frac{k}{T} ) \hspace{0.05cm}.$$ | ||
| − | *Die Laufvariable $k = 0$ gibt die ursprüngliche Spektralfunktion $G(f)$ an. Diese ist grau gefüllt. | + | *Die Laufvariable $k = 0$ gibt die ursprüngliche Spektralfunktion $G(f)$ an. Diese ist grau gefüllt. |
| − | *Das um den Wert $1/T = 10\, \rm kHz$ nach rechts verschobene Spektrum gehört zu $k = 1$ und ist grün markiert, während $k = -1$ zur gelb hinterlegten Funktion führt. | + | *Das um den Wert $1/T = 10\, \rm kHz$ nach rechts verschobene Spektrum gehört zu $k = 1$ und ist grün markiert, während $k = -1$ zur gelb hinterlegten Funktion führt. |
| − | *Die roten und blauen Flächen kennzeichnen die Beiträge der Laufvariablen $k = 2$ und $k = - 2$. | + | *Die roten und blauen Flächen kennzeichnen die Beiträge der Laufvariablen $k = 2$ und $k = - 2$. |
| − | + | Man erkennt, dass $G_{\rm Per}(f)$ konstant ist. Daraus folgt, dass das erste Nyquistkriterium erfüllt ist. Richtig ist demzufolge der <u>Lösungsvorschlag 1</u>. | |
| − | Man erkennt, dass $G_{\rm Per}(f)$ konstant ist. Daraus folgt, dass das erste Nyquistkriterium erfüllt ist. Richtig ist demzufolge der <u>Lösungsvorschlag 1</u>. | ||
'''(2)''' Aufgrund der Fourierintegrale gilt folgender Zusammenhang: | '''(2)''' Aufgrund der Fourierintegrale gilt folgender Zusammenhang: | ||
:$$g(t=0) = \int_{-\infty}^{\infty}G(f) \,{\rm d} f | :$$g(t=0) = \int_{-\infty}^{\infty}G(f) \,{\rm d} f | ||
| − | = A \cdot ( 2\,{\rm kHz}+6\,{\rm kHz}+2\,{\rm kHz})= A \cdot 10\,{\rm kHz} | + | = A \cdot ( 2\,{\rm kHz}+6\,{\rm kHz}+2\,{\rm kHz})= A \cdot 10\,{\rm kHz}$$ |
| − | \Rightarrow \hspace{0.3cm}A = \frac{g(t=0)}{10\,{\rm kHz}} = \frac{2\,{\rm V}}{10\,{\rm kHz}} \hspace{0.1cm}\underline {= 0.2 \, {\rm mV/Hz}} \hspace{0.05cm}.$$ | + | :$$\Rightarrow \hspace{0.3cm}A = \frac{g(t=0)}{10\,{\rm kHz}} = \frac{2\,{\rm V}}{10\,{\rm kHz}} \hspace{0.1cm}\underline {= 0.2 \, {\rm mV/Hz}} \hspace{0.05cm}.$$ |
| − | '''(3)''' Es gelte $g(t) = g_{1}(t) +g_{2}(t)$, wobei | + | '''(3)''' Es gelte $g(t) = g_{1}(t) +g_{2}(t)$, wobei |
| − | *$g_{1}(t)$ die Spektralanteile im Intervall $\pm 3 \, \rm kHz$ beinhaltet und | + | *$g_{1}(t)$ die Spektralanteile im Intervall $\pm 3 \, \rm kHz$ beinhaltet und |
| − | *$g_{2}(t)$ diejenigen zwischen $13 \, \rm kHz$ und $15 \, \rm kHz$ ( | + | *$g_{2}(t)$ diejenigen zwischen $13 \, \rm kHz$ und $15 \, \rm kHz$ (sowie zwischen $-13 \, \rm kHz$ und $-15 \, \rm kHz$). |
| Zeile 98: | Zeile 99: | ||
\\ {\rm{f\ddot{u}r}}\hspace{0.15cm}|f| > 1\,{\rm kHz} \hspace{0.05cm}. \\ | \\ {\rm{f\ddot{u}r}}\hspace{0.15cm}|f| > 1\,{\rm kHz} \hspace{0.05cm}. \\ | ||
\end{array}$$ | \end{array}$$ | ||
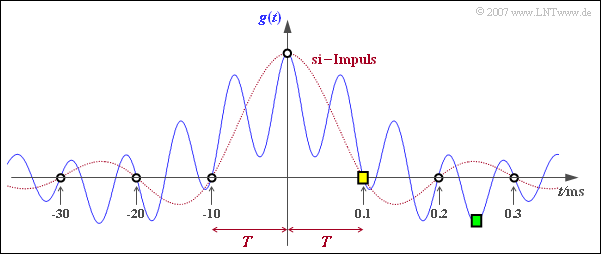
| − | Die untere Grafik zeigt den numerisch ermittelten Zeitverlauf $g(t)$. Für den Zeitpunkt $t = T = 0.1\, \rm ms$ (gelbes Quadrat) erhält man: | + | Die untere Grafik zeigt den numerisch ermittelten Zeitverlauf $g(t)$. Für den Zeitpunkt $t = T = 0.1\, \rm ms$ (gelbes Quadrat) erhält man: |
:$$g_2(t = T ) = 2A \cdot 2\,{\rm kHz} \cdot {\rm si}(0.2 \cdot \pi | :$$g_2(t = T ) = 2A \cdot 2\,{\rm kHz} \cdot {\rm si}(0.2 \cdot \pi | ||
)\cdot \cos (2.8 \cdot \pi) | )\cdot \cos (2.8 \cdot \pi) | ||
| Zeile 104: | Zeile 105: | ||
)\cdot\cos (0.8 \cdot \pi) = \frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot [{\rm sin}(-0.6 \cdot | )\cdot\cos (0.8 \cdot \pi) = \frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot [{\rm sin}(-0.6 \cdot | ||
\pi)+ {\rm sin}(\pi)] $$ | \pi)+ {\rm sin}(\pi)] $$ | ||
| + | [[Datei:P_ID1281__Dig_A_1_4c.png|right|frame|Höherfrequenter Nyquistimpuls]] | ||
:$$\Rightarrow \hspace{0.3cm} g_2(t = T ) = -\frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot {\rm sin}(0.6 \cdot | :$$\Rightarrow \hspace{0.3cm} g_2(t = T ) = -\frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot {\rm sin}(0.6 \cdot | ||
\pi).$$ | \pi).$$ | ||
Für den ersten Anteil $g_1(t)$ gilt zum Zeitpunkt $t = T$: | Für den ersten Anteil $g_1(t)$ gilt zum Zeitpunkt $t = T$: | ||
| − | :$$g_1(t = T ) = A \cdot 6\,{\rm kHz} \cdot {\rm | + | :$$g_1(t = T ) = A \cdot 6\,{\rm kHz} \cdot {\rm sinc}(0.6 |
| − | + | )$$ | |
| − | )= - g_2(t = T )$$ | + | :$$\Rightarrow \hspace{0.3cm}g_1(t = T ) = \frac{ A \cdot 6\,{\rm kHz}}{0.6 \cdot \pi}\cdot {\rm sin}(0.6 \cdot \pi |
| + | )$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}g_1(t = T ) = - g_2(t = T )$$ | ||
:$$\Rightarrow \hspace{0.3cm} g(t = T ) = g_1(t = T ) + g_2(t = T )\hspace{0.1cm}\underline {= 0 } \hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} g(t = T ) = g_1(t = T ) + g_2(t = T )\hspace{0.1cm}\underline {= 0 } \hspace{0.05cm}.$$ | ||
Dieses Ergebnis ist aufgrund der Nyquisteigenschaft nicht überraschend. | Dieses Ergebnis ist aufgrund der Nyquisteigenschaft nicht überraschend. | ||
| − | |||
| − | '''(4)''' Für $t = 2.5 T$ (grünes Quadrat) erhält man folgende Teilergebnisse: | + | '''(4)''' Für $t = 2.5 T$ (grünes Quadrat) erhält man folgende Teilergebnisse: |
:$$g_1(t = 2.5 T ) = A \cdot 6\,{\rm kHz} \cdot {\rm si}(1.5 \cdot \pi | :$$g_1(t = 2.5 T ) = A \cdot 6\,{\rm kHz} \cdot {\rm si}(1.5 \cdot \pi | ||
)= \frac{ A \cdot 6\,{\rm kHz}}{1.5 \cdot \pi}\cdot {\rm sin}(1.5 \cdot \pi | )= \frac{ A \cdot 6\,{\rm kHz}}{1.5 \cdot \pi}\cdot {\rm sin}(1.5 \cdot \pi | ||
| Zeile 122: | Zeile 125: | ||
)\cdot \cos (7 \cdot \pi)=- \frac{ A \cdot 8\,{\rm kHz}}{ \pi} $$ | )\cdot \cos (7 \cdot \pi)=- \frac{ A \cdot 8\,{\rm kHz}}{ \pi} $$ | ||
:$$\Rightarrow \hspace{0.3cm} g(t = 2.5 T ) = g_1(t = 2.5 T ) +g_2(t = 2.5 T ) = - \frac{ A \cdot 12\,{\rm kHz}}{ \pi} \hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} g(t = 2.5 T ) = g_1(t = 2.5 T ) +g_2(t = 2.5 T ) = - \frac{ A \cdot 12\,{\rm kHz}}{ \pi} \hspace{0.05cm}.$$ | ||
| − | Berücksichtigt man $g(t = 0) = A \cdot 10 \ \rm kHz$, so ergibt sich: | + | Berücksichtigt man $g(t = 0) = A \cdot 10 \ \rm kHz$, so ergibt sich: |
:$$\frac{g(t = 2.5 T )}{g(t = 0)} = -\frac{ 1.2}{ \pi} \hspace{0.1cm}\underline {= -0.382 } \hspace{0.05cm}.$$ | :$$\frac{g(t = 2.5 T )}{g(t = 0)} = -\frac{ 1.2}{ \pi} \hspace{0.1cm}\underline {= -0.382 } \hspace{0.05cm}.$$ | ||
| − | '''(5)''' Das zweite Nyquistkriterium besagt, dass der Nyquistimpuls $g(t)$ Nulldurchgänge bei $\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ besitzt. | + | '''(5)''' Das zweite Nyquistkriterium besagt, dass der Nyquistimpuls $g(t)$ Nulldurchgänge bei $\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ besitzt. |
| − | *Nach dem Ergebnis aus '''(4)''' ist diese Bedingung hier nicht erfüllt. | + | *Nach dem Ergebnis aus '''(4)''' ist diese Bedingung hier nicht erfüllt. Richtig ist demzufolge der <u>Lösungsvorschlag 2</u>. |
| − | |||
Aktuelle Version vom 1. Mai 2022, 17:01 Uhr
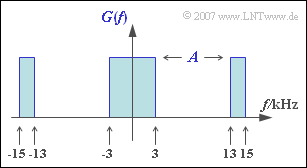
Durch die Skizze gegeben ist das Spektrum $G(f)$ des Detektionsgrundimpulses, wobei der Parameter $A$ noch zu bestimmen ist. Überprüft werden soll unter anderem, ob dieser Detektionsgrundimpuls eines der beiden Nyquistkriterien erfüllt. Diese lauten:
- Das erste Nyquistkriterium ist erfüllt, wenn für die Spektralfunktion gilt:
- $$\sum_{k = -\infty}^{+\infty} G(f - {k}/{T} ) = {\rm const.}$$
- In diesem Fall besitzt der Impuls $g(t)$ für alle ganzzahligen Werte von $ν$ mit Ausnahme von $ν = 0$ Nulldurchgänge bei $t = ν \cdot T$. Für die gesamte Aufgabe wird $T = 0.1 \, \rm ms$ vorausgesetzt.
- Ist das zweite Nyquistkriterium erfüllt, so hat $g(t)$ Nulldurchgänge bei $\pm 1.5 T$, $\pm 2.5 T$, usw.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Eigenschaften von Nyquistsystemen".
- Als bekannt vorausgesetzt werden die beiden Gleichungen:
- $$X(f) = \left\{ \begin{array}{c} A \\ 0 \\\end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\hspace{0.15cm}|f| < f_0 \hspace{0.05cm}, \\ {\rm{f\ddot{u}r}}\hspace{0.15cm}|f| > f_0 \hspace{0.08cm} \\ \end{array} \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} x(t) =2 \cdot A \cdot f_0 \cdot {\rm si}(2 \pi f_0 T) \hspace{0.05cm},\hspace{0.4cm} {\rm si} (x) = \sin(x)/x\hspace{0.05cm},$$
- $$\sin(\alpha) \cdot \cos (\beta) = \frac{1}{2} \cdot \big[ \sin(\alpha - \beta) + \sin(\alpha + \beta)\big] \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} G(f - \frac{k}{T} ) \hspace{0.05cm}.$$
- Die Laufvariable $k = 0$ gibt die ursprüngliche Spektralfunktion $G(f)$ an. Diese ist grau gefüllt.
- Das um den Wert $1/T = 10\, \rm kHz$ nach rechts verschobene Spektrum gehört zu $k = 1$ und ist grün markiert, während $k = -1$ zur gelb hinterlegten Funktion führt.
- Die roten und blauen Flächen kennzeichnen die Beiträge der Laufvariablen $k = 2$ und $k = - 2$.
Man erkennt, dass $G_{\rm Per}(f)$ konstant ist. Daraus folgt, dass das erste Nyquistkriterium erfüllt ist. Richtig ist demzufolge der Lösungsvorschlag 1.
(2) Aufgrund der Fourierintegrale gilt folgender Zusammenhang:
- $$g(t=0) = \int_{-\infty}^{\infty}G(f) \,{\rm d} f = A \cdot ( 2\,{\rm kHz}+6\,{\rm kHz}+2\,{\rm kHz})= A \cdot 10\,{\rm kHz}$$
- $$\Rightarrow \hspace{0.3cm}A = \frac{g(t=0)}{10\,{\rm kHz}} = \frac{2\,{\rm V}}{10\,{\rm kHz}} \hspace{0.1cm}\underline {= 0.2 \, {\rm mV/Hz}} \hspace{0.05cm}.$$
(3) Es gelte $g(t) = g_{1}(t) +g_{2}(t)$, wobei
- $g_{1}(t)$ die Spektralanteile im Intervall $\pm 3 \, \rm kHz$ beinhaltet und
- $g_{2}(t)$ diejenigen zwischen $13 \, \rm kHz$ und $15 \, \rm kHz$ (sowie zwischen $-13 \, \rm kHz$ und $-15 \, \rm kHz$).
Mit der angegebenen Fourierkorrespondenz lauten die beiden Anteile:
- $$g_1(t) \ = \ A \cdot 6\,{\rm kHz} \cdot {\rm si}(\pi \cdot 6\,{\rm kHz} \cdot t) \hspace{0.05cm},$$
- $$g_2(t) \ = \ A \cdot 2\,{\rm kHz} \cdot{\rm si}(\pi \cdot 2\,{\rm kHz} \cdot t) \cdot 2 \cdot {\rm cos}(2 \pi \cdot 14\,{\rm kHz} \cdot t) \hspace{0.05cm}.$$
Die zweite Gleichung folgt aus der Beziehung:
- $$G_2(f) = \left[ \delta(f + 14\,{\rm kHz}) + \delta(f - 14\,{\rm kHz})\right] \star \left\{ \begin{array}{c} A \\ 0 \\\end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\hspace{0.15cm}|f| < 1\,{\rm kHz} \hspace{0.05cm}, \\ {\rm{f\ddot{u}r}}\hspace{0.15cm}|f| > 1\,{\rm kHz} \hspace{0.05cm}. \\ \end{array}$$
Die untere Grafik zeigt den numerisch ermittelten Zeitverlauf $g(t)$. Für den Zeitpunkt $t = T = 0.1\, \rm ms$ (gelbes Quadrat) erhält man:
- $$g_2(t = T ) = 2A \cdot 2\,{\rm kHz} \cdot {\rm si}(0.2 \cdot \pi )\cdot \cos (2.8 \cdot \pi) = \frac{ A \cdot 4\,{\rm kHz}}{0.2 \cdot \pi}\cdot {\rm sin}(0.2 \cdot \pi )\cdot\cos (0.8 \cdot \pi) = \frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot [{\rm sin}(-0.6 \cdot \pi)+ {\rm sin}(\pi)] $$
- $$\Rightarrow \hspace{0.3cm} g_2(t = T ) = -\frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot {\rm sin}(0.6 \cdot \pi).$$
Für den ersten Anteil $g_1(t)$ gilt zum Zeitpunkt $t = T$:
- $$g_1(t = T ) = A \cdot 6\,{\rm kHz} \cdot {\rm sinc}(0.6 )$$
- $$\Rightarrow \hspace{0.3cm}g_1(t = T ) = \frac{ A \cdot 6\,{\rm kHz}}{0.6 \cdot \pi}\cdot {\rm sin}(0.6 \cdot \pi )$$
- $$\Rightarrow \hspace{0.3cm}g_1(t = T ) = - g_2(t = T )$$
- $$\Rightarrow \hspace{0.3cm} g(t = T ) = g_1(t = T ) + g_2(t = T )\hspace{0.1cm}\underline {= 0 } \hspace{0.05cm}.$$
Dieses Ergebnis ist aufgrund der Nyquisteigenschaft nicht überraschend.
(4) Für $t = 2.5 T$ (grünes Quadrat) erhält man folgende Teilergebnisse:
- $$g_1(t = 2.5 T ) = A \cdot 6\,{\rm kHz} \cdot {\rm si}(1.5 \cdot \pi )= \frac{ A \cdot 6\,{\rm kHz}}{1.5 \cdot \pi}\cdot {\rm sin}(1.5 \cdot \pi )= - \frac{ A \cdot 4\,{\rm kHz}}{ \pi}\hspace{0.05cm},$$
- $$g_2(t = 2.5 T ) = 2A \cdot 2\,{\rm kHz} \cdot {\rm si}(0.5 \cdot \pi )\cdot \cos (7 \cdot \pi)=- \frac{ A \cdot 8\,{\rm kHz}}{ \pi} $$
- $$\Rightarrow \hspace{0.3cm} g(t = 2.5 T ) = g_1(t = 2.5 T ) +g_2(t = 2.5 T ) = - \frac{ A \cdot 12\,{\rm kHz}}{ \pi} \hspace{0.05cm}.$$
Berücksichtigt man $g(t = 0) = A \cdot 10 \ \rm kHz$, so ergibt sich:
- $$\frac{g(t = 2.5 T )}{g(t = 0)} = -\frac{ 1.2}{ \pi} \hspace{0.1cm}\underline {= -0.382 } \hspace{0.05cm}.$$
(5) Das zweite Nyquistkriterium besagt, dass der Nyquistimpuls $g(t)$ Nulldurchgänge bei $\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ besitzt.
- Nach dem Ergebnis aus (4) ist diese Bedingung hier nicht erfüllt. Richtig ist demzufolge der Lösungsvorschlag 2.