Aufgaben:Aufgabe 1.2Z: Nochmals Lognormal–Fading: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Mobile Kommunikation/Distanzabhängige Dämpfung und Abschattung }} right|frame Wir gehen von ähn…“) |
|||
| Zeile 4: | Zeile 4: | ||
[[Datei:P_ID2123__Mob_Z_1_2.png|right|frame]] | [[Datei:P_ID2123__Mob_Z_1_2.png|right|frame]] | ||
| − | Wir gehen von ähnlichen Bedingungen wie in der [[Aufgaben:1.2_Lognormal_%E2%80%93_Kanalmodell|Aufgabe A1.2]] aus, fassen aber nun den rein entfernungsabhängigen Pfadverlust | + | Wir gehen von ähnlichen Bedingungen wie in der [[Aufgaben:1.2_Lognormal_%E2%80%93_Kanalmodell|Aufgabe A1.2]] aus, fassen aber nun den rein entfernungsabhängigen Pfadverlust $V_0$ und den Mittelwert $m_S$ des Lognormal–Fadings zusammen (der Index S steht für <i>Shadowing</i>): |
:$$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$ | :$$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$ | ||
| Zeile 10: | Zeile 10: | ||
:$$V_{\rm P} = V_{\rm 1} + V_{\rm 2}(t)$$ | :$$V_{\rm P} = V_{\rm 1} + V_{\rm 2}(t)$$ | ||
| − | gegeben, wobei | + | gegeben, wobei $V_2(t)$ eine<span style="color: rgb(204, 0, 0);"> <b>Lognormal–Verteilung mit Mittelwert 0</b> </span>beschreibt: |
:$$f_{V{\rm 2}}(V_{\rm 2}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ V_{\rm 2} ^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}.$$ | :$$f_{V{\rm 2}}(V_{\rm 2}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ V_{\rm 2} ^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}.$$ | ||
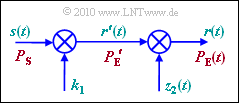
| − | Das in der Grafik gezeigte Pfadverlustmodell ist für das hier beschriebene Szenario geeignet. Multipliziert man das Sendesignal | + | Das in der Grafik gezeigte Pfadverlustmodell ist für das hier beschriebene Szenario geeignet. Multipliziert man das Sendesignal $s(t)$ zunächst mit einem konstanten Faktor $k_1$ und weiter mit einer stochastischen Größe $z_2(t)$ mit der Wahrscheinlichkeitsdichte $f_{\rm z2}(z_2)$, so ergibt sich am Ausgang das Signal $r(t)$, dessen Leistung $P_E(t)$ aufgrund des stochastischen Anteils natürlich ebenfalls zeitabhängig ist. Die WDF der lognormalverteilten Zufallsgröße $z_2$ lautet für $z_2 ≥ 0$: |
:$$f_{z{\rm 2}}(z_{\rm 2}) = \frac {{\rm exp } \left [ - {\rm ln}^2 (z_{\rm 2}) /({2 \cdot C^2 \cdot \sigma_{\rm S}^2}) \right ]}{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot z_2} \hspace{0.3cm}{\rm mit} \hspace{0.3cm} C = \frac{{\rm ln} \hspace{0.1cm}(10)}{20\,\,{\rm dB}}\hspace{0.05cm}.$$ | :$$f_{z{\rm 2}}(z_{\rm 2}) = \frac {{\rm exp } \left [ - {\rm ln}^2 (z_{\rm 2}) /({2 \cdot C^2 \cdot \sigma_{\rm S}^2}) \right ]}{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot z_2} \hspace{0.3cm}{\rm mit} \hspace{0.3cm} C = \frac{{\rm ln} \hspace{0.1cm}(10)}{20\,\,{\rm dB}}\hspace{0.05cm}.$$ | ||
| − | Für | + | Für $z_2 ≤ 0$ ist diese WDF identisch 0. |
''Hinweis:'' Die Aufgabe gehört zum [[Mobile_Kommunikation/Distanzabh%C3%A4ngige_D%C3%A4mpfung_und_Abschattung|Kapitel 1.1]]. | ''Hinweis:'' Die Aufgabe gehört zum [[Mobile_Kommunikation/Distanzabh%C3%A4ngige_D%C3%A4mpfung_und_Abschattung|Kapitel 1.1]]. | ||
| Zeile 22: | Zeile 22: | ||
:$$V_{\rm 1} = 60\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 6\,{\rm dB}\hspace{0.05cm}.$$ | :$$V_{\rm 1} = 60\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 6\,{\rm dB}\hspace{0.05cm}.$$ | ||
| − | Die Wahrscheinlichkeit, dass eine mittelwertfreie Gaußsche Zufallsgröße | + | Die Wahrscheinlichkeit, dass eine mittelwertfreie Gaußsche Zufallsgröße $z$ einen größeren Wert besitzt als ihre Streuung $\sigma$, ist bekanntlich |
:$${\rm Pr}(z > \sigma) = {\rm Pr}(z < -\sigma) = {\rm Q}(1) \approx 0.158\hspace{0.05cm}.$$ | :$${\rm Pr}(z > \sigma) = {\rm Pr}(z < -\sigma) = {\rm Q}(1) \approx 0.158\hspace{0.05cm}.$$ | ||
| Zeile 28: | Zeile 28: | ||
:$${\rm Pr}(z > 2\sigma) = {\rm Pr}(z < -2\sigma) = {\rm Q}(2) \approx 0.023\hspace{0.05cm}.$$ | :$${\rm Pr}(z > 2\sigma) = {\rm Pr}(z < -2\sigma) = {\rm Q}(2) \approx 0.023\hspace{0.05cm}.$$ | ||
| − | Nochmals zur Verdeutlichung: | + | Nochmals zur Verdeutlichung: $z_2$ ist die lineare Fading–Größe, während die Beschreibungsgröße $V_2$ auf dem Zehner–Logarithmus basiert. Es gelten folgende Umrechnungen: |
:$$z_2 = 10^{-V_{\rm 2}/20\,{\rm dB}}\hspace{0.05cm}, \hspace{0.2cm} | :$$z_2 = 10^{-V_{\rm 2}/20\,{\rm dB}}\hspace{0.05cm}, \hspace{0.2cm} | ||
V_{\rm 2} = -20\,{\rm dB} \cdot {\rm lg}\hspace{0.15cm}z_2\hspace{0.05cm}.$$ | V_{\rm 2} = -20\,{\rm dB} \cdot {\rm lg}\hspace{0.15cm}z_2\hspace{0.05cm}.$$ | ||
{{Display}} | {{Display}} | ||
Version vom 22. Oktober 2017, 15:11 Uhr
Wir gehen von ähnlichen Bedingungen wie in der Aufgabe A1.2 aus, fassen aber nun den rein entfernungsabhängigen Pfadverlust $V_0$ und den Mittelwert $m_S$ des Lognormal–Fadings zusammen (der Index S steht für Shadowing):
- $$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$
Der gesamte Pfadverlust ist dann durch die Gleichung
- $$V_{\rm P} = V_{\rm 1} + V_{\rm 2}(t)$$
gegeben, wobei $V_2(t)$ eine Lognormal–Verteilung mit Mittelwert 0 beschreibt:
- $$f_{V{\rm 2}}(V_{\rm 2}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ V_{\rm 2} ^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}.$$
Das in der Grafik gezeigte Pfadverlustmodell ist für das hier beschriebene Szenario geeignet. Multipliziert man das Sendesignal $s(t)$ zunächst mit einem konstanten Faktor $k_1$ und weiter mit einer stochastischen Größe $z_2(t)$ mit der Wahrscheinlichkeitsdichte $f_{\rm z2}(z_2)$, so ergibt sich am Ausgang das Signal $r(t)$, dessen Leistung $P_E(t)$ aufgrund des stochastischen Anteils natürlich ebenfalls zeitabhängig ist. Die WDF der lognormalverteilten Zufallsgröße $z_2$ lautet für $z_2 ≥ 0$:
- $$f_{z{\rm 2}}(z_{\rm 2}) = \frac {{\rm exp } \left [ - {\rm ln}^2 (z_{\rm 2}) /({2 \cdot C^2 \cdot \sigma_{\rm S}^2}) \right ]}{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot z_2} \hspace{0.3cm}{\rm mit} \hspace{0.3cm} C = \frac{{\rm ln} \hspace{0.1cm}(10)}{20\,\,{\rm dB}}\hspace{0.05cm}.$$
Für $z_2 ≤ 0$ ist diese WDF identisch 0.
Hinweis: Die Aufgabe gehört zum Kapitel 1.1. Verwenden Sie folgende Kenngrößen:
- $$V_{\rm 1} = 60\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 6\,{\rm dB}\hspace{0.05cm}.$$
Die Wahrscheinlichkeit, dass eine mittelwertfreie Gaußsche Zufallsgröße $z$ einen größeren Wert besitzt als ihre Streuung $\sigma$, ist bekanntlich
- $${\rm Pr}(z > \sigma) = {\rm Pr}(z < -\sigma) = {\rm Q}(1) \approx 0.158\hspace{0.05cm}.$$
Weiterhin gilt:
- $${\rm Pr}(z > 2\sigma) = {\rm Pr}(z < -2\sigma) = {\rm Q}(2) \approx 0.023\hspace{0.05cm}.$$
Nochmals zur Verdeutlichung: $z_2$ ist die lineare Fading–Größe, während die Beschreibungsgröße $V_2$ auf dem Zehner–Logarithmus basiert. Es gelten folgende Umrechnungen:
- $$z_2 = 10^{-V_{\rm 2}/20\,{\rm dB}}\hspace{0.05cm}, \hspace{0.2cm} V_{\rm 2} = -20\,{\rm dB} \cdot {\rm lg}\hspace{0.15cm}z_2\hspace{0.05cm}.$$