Aufgaben:Aufgabe 1.11Z: Nochmals Syndromdecodierung: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
[[Datei:P_ID2399__KC_Z_1_10.png|right|frame|Schaubild: Prüfgleichungen]] | [[Datei:P_ID2399__KC_Z_1_10.png|right|frame|Schaubild: Prüfgleichungen]] | ||
| − | Betrachtet wird die gleiche Konstellation wie in [[Aufgaben:1.11_Syndromdecodierung|Aufgabe 1.11]], nämlich die Decodierung eines $(7, 4, 3)$–Hamming–Codes mit der Prüfmatrix | + | Betrachtet wird die gleiche Konstellation wie in [[Aufgaben:1.11_Syndromdecodierung|"Aufgabe 1.11"]], nämlich die Decodierung eines $(7, 4, 3)$–Hamming–Codes mit der Prüfmatrix |
:$${ \boldsymbol{\rm H}}_{\rm } = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$ | :$${ \boldsymbol{\rm H}}_{\rm } = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$ | ||
| − | Dementsprechend lautet | + | Dementsprechend lautet die Generatormatrix: |
:$${ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$ | :$${ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$ | ||
| − | Bei der [[Kanalcodierung/Decodierung_linearer_Blockcodes#Prinzip_der_Syndromdecodierung|Syndromdecodierung]] bildet man aus dem Empfangsvektor $\underline{y}$ das Syndrom $\underline{s}$ entsprechend der Gleichung | + | Bei der [[Kanalcodierung/Decodierung_linearer_Blockcodes#Prinzip_der_Syndromdecodierung|"Syndromdecodierung"]] bildet man aus dem Empfangsvektor $\underline{y}$ das Syndrom $\underline{s}$ entsprechend der Gleichung |
:$$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} \in {\rm GF}(2^m) \hspace{0.05cm}.$$ | :$$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} \in {\rm GF}(2^m) \hspace{0.05cm}.$$ | ||
Mit diesem Ergebnis lässt sich beim betrachteten Hamming–Code ein jeder Einzelfehler im Codewort korrigieren. | Mit diesem Ergebnis lässt sich beim betrachteten Hamming–Code ein jeder Einzelfehler im Codewort korrigieren. | ||
| − | *Im fehlerfreien Fall gilt $\underline{s} = \underline{s}_{0} = (0, 0, 0)$. | + | *Im fehlerfreien Fall gilt $\underline{s} = \underline{s}_{0} = (0, 0, 0)$. |
| + | |||
*Aber auch bei drei Übertragungsfehlern kann sich unter Umständen $\underline{s}_{0} = (0, 0, 0)$ ergeben, so dass diese Fehler unerkannt bleiben. | *Aber auch bei drei Übertragungsfehlern kann sich unter Umständen $\underline{s}_{0} = (0, 0, 0)$ ergeben, so dass diese Fehler unerkannt bleiben. | ||
| Zeile 22: | Zeile 23: | ||
| − | + | Hinweise: | |
| − | + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Decodierung_linearer_Blockcodes|"Decodierung linearer Blockcodes"]]. | |
| − | + | ||
| − | + | * Weitere Informationen zur Syndromdecodierung finden Sie im Angabenblatt zur [[Aufgaben:1.11_Syndromdecodierung|"Aufgabe 1.11"]]. | |
| − | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Decodierung_linearer_Blockcodes|Decodierung linearer Blockcodes]]. | + | |
| − | * Weitere Informationen zur Syndromdecodierung finden Sie im Angabenblatt zur [[Aufgaben:1.11_Syndromdecodierung|Aufgabe 1.11]]. | ||
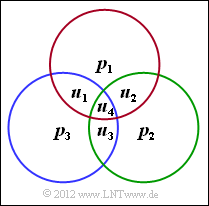
* Die Grafik verdeutlicht die drei Prüfgleichungen entsprechend der Prüfmatrix: | * Die Grafik verdeutlicht die drei Prüfgleichungen entsprechend der Prüfmatrix: | ||
| − | **erste Zeile: rote Gruppierung, | + | **erste Zeile: rote Gruppierung, |
| − | **zweite Zeile: grüne Gruppierung, | + | **zweite Zeile: grüne Gruppierung, |
| − | **dritte Zeile: blaue Gruppierung. | + | **dritte Zeile: blaue Gruppierung. |
Version vom 20. Juli 2022, 13:17 Uhr
Betrachtet wird die gleiche Konstellation wie in "Aufgabe 1.11", nämlich die Decodierung eines $(7, 4, 3)$–Hamming–Codes mit der Prüfmatrix
- $${ \boldsymbol{\rm H}}_{\rm } = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$
Dementsprechend lautet die Generatormatrix:
- $${ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$
Bei der "Syndromdecodierung" bildet man aus dem Empfangsvektor $\underline{y}$ das Syndrom $\underline{s}$ entsprechend der Gleichung
- $$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} \in {\rm GF}(2^m) \hspace{0.05cm}.$$
Mit diesem Ergebnis lässt sich beim betrachteten Hamming–Code ein jeder Einzelfehler im Codewort korrigieren.
- Im fehlerfreien Fall gilt $\underline{s} = \underline{s}_{0} = (0, 0, 0)$.
- Aber auch bei drei Übertragungsfehlern kann sich unter Umständen $\underline{s}_{0} = (0, 0, 0)$ ergeben, so dass diese Fehler unerkannt bleiben.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Decodierung linearer Blockcodes".
- Weitere Informationen zur Syndromdecodierung finden Sie im Angabenblatt zur "Aufgabe 1.11".
- Die Grafik verdeutlicht die drei Prüfgleichungen entsprechend der Prüfmatrix:
- erste Zeile: rote Gruppierung,
- zweite Zeile: grüne Gruppierung,
- dritte Zeile: blaue Gruppierung.
Fragebogen
Musterlösung
- Diese beinhaltet am Ende eine $3×3$–Diagonalmatrix.
- Die Codeworte lauten demzufolge:
- $$ \underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_{3}) \hspace{0.05cm}.$$
(2) Mit diesem Empfangsvektor $\underline{y} = (1, 0, 0, 1, 0, 1, 0)$ werden alle Prüfgleichungen erfüllt:
- $$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$
- $$u_2 \oplus u_3 \oplus u_4 \oplus p_2 = 0 \oplus 0 \oplus 1 \oplus 1 = 0 \hspace{0.05cm},$$
- $$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm}.$$
Richtig ist dementsprechend die Antwort JA.
(3) Es gilt $\underline{s} = \underline{y} · \boldsymbol{\rm H}^{\rm T}$:
- $$ \underline{s} = \begin{pmatrix} 1 &0 &0 &1 &0 &1 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 &0 &1\\ 1 &1 &0\\ 0 &1 &1\\ 1 &1 &1\\ 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} = \begin{pmatrix} 0 &0 &0 \end{pmatrix} = \underline{s}_0 \hspace{0.2cm} \Rightarrow\hspace{0.2cm} \hspace{0.15cm} \underline{ \rm Antwort \hspace{0.15cm}1} \hspace{0.05cm}.$$
(4) Man könnte nun für jedes $\underline{y}$ die Gleichung $\underline{y} · \boldsymbol{\rm H}^{\rm T} = (0, 0, 0)$ überprüfen. Hier soll nun das Ergebnis auf anderem Wege gewonnen werden:
- $\underline{y}= (1, 1, 0, 1, 0, 1, 0)$ unterscheidet sich von $\underline{y} = (1, 0, 0, 1, 0, 1, 0)$ im Bit $u_{2}$, das nur in den beiden ersten Prüfgleichungen verwendet wird, nicht jedoch in der letzten ⇒ $\underline{s} = \underline{s}_{6} = (1, 1, 0)$.
- Wendet man die Prüfgleichungen auf $\underline{y} = (0, 1, 0, 1, 0, 0, 1)$ an, so erhält man $\underline{s} = \underline{s}_{0} = (0, 0, 0)$, wie die folgende Rechnung belegt:
- $$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 0 \oplus 1 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$
- $$u_2 \oplus u_3 \oplus u_4 \oplus p_2 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$
- $$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 0 \oplus 0 \oplus 1 \oplus 1 = 0 \hspace{0.05cm}.$$
- Zum gleichen Ergebnis kommt man mit dem Empfangsvektor $\underline{y} = (0, 1, 1, 0, 1, 0, 1),$ der sich vom Vektor $(1, 0, 0, 1, 0, 1, 0)$ in allen sieben Bitpositionen unterscheidet:
- $$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 0 \oplus 1 \oplus 0 \oplus 1 = 0 \hspace{0.05cm},$$
- $$u_2 \oplus u_3 \oplus u_4 \oplus p_2 = 1 \oplus 1 \oplus 0 \oplus 0 = 0 \hspace{0.05cm},$$
- $$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 0 \oplus 1 \oplus 0 \oplus 1 = 0 \hspace{0.05cm}.$$
Richtig sind also die Antworten 2 und 3.