Aufgabe 2.1Z: 2D-Frequenz- und 2D-Zeitdarstellung: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
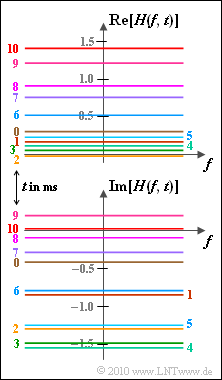
[[Datei:P_ID2145__Mob_z_2_1.png|right|frame|2D–Übertragungsfunktion, als Realteil und Imaginärteil]] | [[Datei:P_ID2145__Mob_z_2_1.png|right|frame|2D–Übertragungsfunktion, als Realteil und Imaginärteil]] | ||
| − | Zur Beschreibung eines zeitvarianten Kanals mit mehreren Pfaden verwendet man die | + | Zur Beschreibung eines zeitvarianten Kanals mit mehreren Pfaden verwendet man die ''zweidimensionale Impulsantwort'' |
| − | :$$h(\tau,\hspace{0. | + | :$$h(\tau,\hspace{0.1cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)\hspace{0.05cm}.$$ |
Der erste Parameter $(\tau)$ kennzeichnet die Verzögerungszeit, der zweite $(t)$ macht Aussagen über die Zeitvarianz. | Der erste Parameter $(\tau)$ kennzeichnet die Verzögerungszeit, der zweite $(t)$ macht Aussagen über die Zeitvarianz. | ||
| − | Durch die Fouriertransformation von $h(\tau, t)$ kommt man schließlich zur | + | Durch die Fouriertransformation von $h(\tau,\ t)$ kommt man schließlich zur ''zeitvarianten Übertragungsfunktion'' |
| − | :$$H(f,\hspace{0. | + | :$$H(f,\hspace{0.1cm} t) |
| − | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0. | + | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.1cm}t) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In der Grafik ist $H(f, t)$ in Abhängigkeit der Frequenz dargestellt, und zwar für verschiedene Werte der absoluten Zeit $t$ im Bereich von $0 \ \text{...} \ 10 \ \rm ms$. | + | In der Grafik ist $H(f,\ t)$ in Abhängigkeit der Frequenz dargestellt, und zwar für verschiedene Werte der absoluten Zeit $t$ im Bereich von $0 \ \text{...} \ 10 \ \rm ms$. |
| + | |||
| + | Im Allgemeinen ist $H(f,\ t)$ komplex. Der Realteil (oben) und der Imaginärteil (unten) sind separat gezeichnet. | ||
| + | |||
| + | |||
| − | |||
| Zeile 34: | Zeile 37: | ||
H(f,\hspace{0.05cm} t = 10\, {\rm ms}) \approx 1.4 \hspace{0.05cm}.$$ | H(f,\hspace{0.05cm} t = 10\, {\rm ms}) \approx 1.4 \hspace{0.05cm}.$$ | ||
| − | * Wie schon aus obiger Grafik zu erahnen ist, sind weder der Realteil noch der Imaginärteil der 2D–Übertragungsfunktion $H(f, t)$ mittelwertfrei. | + | * Wie schon aus obiger Grafik zu erahnen ist, sind weder der Realteil noch der Imaginärteil der 2D–Übertragungsfunktion $H(f,\ t)$ mittelwertfrei. |
| Zeile 52: | Zeile 55: | ||
{Wie kann hier die 2D–Impulsantwort beschrieben werden? | {Wie kann hier die 2D–Impulsantwort beschrieben werden? | ||
|type="[]"} | |type="[]"} | ||
| − | - $h(\tau, t) = A \cdot \delta(\tau) + B \cdot \delta(\tau \, –5 \, \rm µ s)$. | + | - $h(\tau,\ t) = A \cdot \delta(\tau) + B \cdot \delta(\tau \, –5 \, \rm µ s)$. |
| − | - $h(\tau, t) = A \cdot \delta(\tau)$. | + | - $h(\tau,\ t) = A \cdot \delta(\tau)$. |
| − | + $h(\tau, t) = z(t) \cdot \delta(\tau)$. | + | + $h(\tau,\ t) = z(t) \cdot \delta(\tau)$. |
{Schätzen Sie, für welchen Kanal die Daten aufgenommen wurden. | {Schätzen Sie, für welchen Kanal die Daten aufgenommen wurden. | ||
Version vom 13. Mai 2020, 17:41 Uhr
Zur Beschreibung eines zeitvarianten Kanals mit mehreren Pfaden verwendet man die zweidimensionale Impulsantwort
- $$h(\tau,\hspace{0.1cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)\hspace{0.05cm}.$$
Der erste Parameter $(\tau)$ kennzeichnet die Verzögerungszeit, der zweite $(t)$ macht Aussagen über die Zeitvarianz.
Durch die Fouriertransformation von $h(\tau,\ t)$ kommt man schließlich zur zeitvarianten Übertragungsfunktion
- $$H(f,\hspace{0.1cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.1cm}t) \hspace{0.05cm}.$$
In der Grafik ist $H(f,\ t)$ in Abhängigkeit der Frequenz dargestellt, und zwar für verschiedene Werte der absoluten Zeit $t$ im Bereich von $0 \ \text{...} \ 10 \ \rm ms$.
Im Allgemeinen ist $H(f,\ t)$ komplex. Der Realteil (oben) und der Imaginärteil (unten) sind separat gezeichnet.
Hinweise:
- Die Aufgabe gehört zum Themengebiet des Kapitels Allgemeine Beschreibung zeitvarianter Systeme.
- In obiger Gleichung wird ein echofreier Kanal mit dem Paramter $M = 1$ dargestellt.
- Hier noch einige Zahlenwerte der vorgegebenen zeitvarianten Übertragungsfunktion:
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\, {\rm ms}) \approx 0.3 - {\rm j} \cdot 0.4 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 2\, {\rm ms}) \approx 0.0 - {\rm j} \cdot 1.3 \hspace{0.05cm},$$
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\, {\rm ms}) \approx 0.1 - {\rm j} \cdot 1.5 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 6\, {\rm ms}) \approx 0.5 - {\rm j} \cdot 0.8 \hspace{0.05cm},$$
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 8\, {\rm ms}) \approx 0.9 - {\rm j} \cdot 0.1 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 10\, {\rm ms}) \approx 1.4 \hspace{0.05cm}.$$
- Wie schon aus obiger Grafik zu erahnen ist, sind weder der Realteil noch der Imaginärteil der 2D–Übertragungsfunktion $H(f,\ t)$ mittelwertfrei.
Fragebogen
Musterlösung
(2) Betrachtet man einen festen Zeitpunkt, zum Beispiel $t = 2 \ \rm ms$, so erhält man für die zeitvariante Übertragungsfunktion
- $$H(f,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \hspace{0.05cm} = {\rm const.}$$
Damit lautet die dazugehörige 2D–Impulsantwort:
- $$h(\tau,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \cdot \delta (\tau) \hspace{0.05cm} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} M = 1 \hspace{0.05cm}.$$
Mit einem Pfad kann es aber nicht zu Mehrwegausbreitung kommen. Das heißt, die richtige Lösung ist NEIN.
(3) Richtig ist der Lösungsvorschlag 3:
- Es liegt hier zwar Zeitvarianz, aber keine Frequenzselektivität vor.
- Die Vorschläge 1 und 2 beschreiben dagegen zeitinvariante Systeme.
(4) Richtig ist der Lösungsvorschlag 4:
- Für den AWGN–Kanal kann keine Übertragungsfunktion angegeben werden.
- Bei einem Zweiwegekanal ist $H(f, t)$ zu keiner Zeit $t$ konstant.
- Da in der $H(f, t)$–Grafik in Real– und Imaginärteil jeweils ein Gleichanteil ungleich Null zu erkennen ist, kann auch der Rayleigh–Kanal ausgeschlossen werden.
- Die Daten für die vorliegende Aufgabe stammen von einem Rice–Kanal mit folgenden Parametern:
- $$\sigma = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} x_0 = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm}y_0 = -{1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} f_{\rm D,\hspace{0.05cm} max} = 100\,\,{\rm Hz}\hspace{0.05cm}.$$