Spreizfolgen für CDMA

Inhaltsverzeichnis

1 Definition der Korrelationsfunktionen
2 Periodische AKF und KKF
3 Beurteilungskriterien für PN–Spreizfolgen
4 PN–Folgen maximaler Länge (1)

Definition der Korrelationsfunktionen

Wichtige Beurteilungskriterien für Spreizfolgen sind die Korrelationsfunktionen. Betrachtet man zwei ergodische Prozesse mit den Musterfunktionen $x(t)$ und $y(t)$ , so gilt für die Kreuzkorrelationsfunktion (KKF) der beiden Prozesse (siehe Kapitel 4.6 im Buch „Stochastische Signaltheorie”): $\varphi_{xy}(\tau)=\overline{x(t)\cdot y(t+\tau)}=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\,\rm d \it t.$

Die überstreichende Linie kennzeichnet hierbei eine Zeitmittelung.

$φ){xy}(τ)$ ist ein quantitatives Maß für die lineare statistische Abhängigkeit der Augenblickswerte von Musterfunktionen $x(t)$ und $y(t + τ)$ der beiden Zufallsprozesse und dient somit der Beschreibung der statistischen Verwandtschaft zwischen diesen. Es gilt:

Sind $x(t)$ und $y(t)$ unkorreliert, so ist $φ_{xy}(τ)$ identisch 0 (das heißt für alle Werte von $τ$ ).
Im allgemeinen ist $φ_{xy}(τ)$ nicht symmetrisch, sondern das KKF–Maximum tritt bei $τ_{\rm max} ≠$ 0 auf.
In diesem Fall ergibt sich die maximale Korrelation durch eine gegenseitige Verschiebung der beiden betrachteten Signale um die Zeit $τ_{\rm max}$ .

Setzt man in obiger Gleichung $y(t) = x(t)$ , so kommt man zur Autokorrelationsfunktion (AKF) $\varphi_{xx}(\tau)=\overline{x(t)\cdot x(t+\tau)}=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot x(t+\tau)\,\,\rm d \it t$

mit folgenden Eigenschaften:

Die AKF ist ein Maß für die inneren statistischen Bindungen eines durch die Musterfunktion $x(t)$ festgelegten stationären und ergodischen Prozesses.
Ist $x(t)$ reell, so ist $φ_{xx}(τ)$ eine reelle gerade Funktion: $φ_{xx}(–τ) = φ_{xx}(τ)$ . Phasenbeziehungen gehen in der AKF verloren. Beschreibt $x(t)$ einen komplexen Prozesse, so ist auch die AKF komplex.
Der Maximalwert der AKF liegt bei $τ =$ 0. Es gilt stets $|φ_{xx}(τ)| ≤ φ_{xx}(0),$ wobei $φ_{xx}(0)$ die Signalleistung $P_x = E[x^2(t)]$ angibt.
Der Gleichanteil eines Signals kann aus dem Grenzwert $(τ → ∞)$ ermittelt werden, so lange das Signal keine periodischen Anteile beinhaltet:

$\overline{ x(t)} = {\rm E}[x(t)] = \sqrt{\lim_{\tau\to\infty}\,\varphi_{xx} (\tau)} \hspace{0.05cm}.$

AKF und KKF beschreiben die inneren Bindungen bzw. die gegenseitigen statistischen Abhängigkeiten im Zeitbereich. Die entsprechenden Beschreibungsfunktionen im Frequenzbereich sind

das Leistungsdichtespektrum ${\it Φ}_{xx}(f)$ , sowie
das Kreuzleistungsdichtespektrum ${\it Φ}_{xy}(f)$ .

Bei ergodischen Prozessen ergeben sich diese als die Fouriertransformierten von AKF und KKF: ${\it \Phi}_{xx}(f) \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm}\varphi_{xx}(\tau)\hspace{0.05cm} ,\hspace{0.3cm} {\it \Phi}_{xy}(f) \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm}\varphi_{xy}(\tau)\hspace{0.05cm}.$

Periodische AKF und KKF

Hinweis: Im Folgenden schreiben wir wie im Buch „Stochastische Signaltheorie” vereinfachend für die AKF $φ_x(τ)$ anstelle von $φ_{xx}(τ)$ und für das LDS ${\it Φ}_x(f)$ anstelle von ${\it Φ}_{xx}(f)$ .

Bei periodischen Signalen kann auf den Grenzübergang bei der AKF– und der KKF–Berechnung verzichtet werden, und man erhält mit der Periodendauer $T_0$ (diese muss für beide Signale gleich sein): $\begin{align*}\varphi_{x}(\tau) & = \frac{1}{T_{\rm 0}}\cdot\int^{T_0}_{0}x(t)\cdot x(t+\tau)\,\,\rm d \it t\hspace{0.05cm} ,\\ \varphi_{xy}(\tau) & = \frac{1}{T_{\rm 0}}\cdot\int^{T_0}_{0}x(t)\cdot y(t+\tau)\,\,\rm d \it t\hspace{0.05cm}.\end{align*}$ In diesem Fall ist die AKF ebenfalls eine periodische Funktion, und man spricht von der periodischen Autokorrelationsfunktion (PAKF). Diese zeigt folgende Einenschaft: $\varphi_{x}(\pm T_0) = \varphi_{x}(\pm 2T_0) = ... = \varphi_{x}(0) \hspace{0.05cm}.$ Wir wenden nun obige Berechnungsvorschrift auf das Spreizsignal $c(t) = \sum\limits^{+\infty}_{\nu = -\infty}c_\nu\cdot g_c(t - \nu \cdot T_c)$ an, wobei ein Rechteckimpuls $g_c(t)$ der Breite $T_c$ vorausgesetzt wird; $T_c$ nennt man die Chipdauer. Berücksichtigt man die Periodizität $(T_0 = P · T_c)$ der Amplitudenkoeffizienten $c_ν ∈$ {±1}, so ergeben sich die diskreten AKF–Werte bei Vielfachen von $T_c$ mit dem Parameter $λ$ : $\varphi_{c}(\lambda \cdot T_c) = \frac{1}{P}\cdot\sum\limits^{P-1}_{\nu = 0} c_\nu \cdot c_{\nu+ {\it \lambda} }\hspace{0.05cm}.$ Der maximale PAKF–Wert ergibt sich für $λ =$ 0 und für Vielfache der Periodenlänge $P$ . Aufgrund des rechteckigen Impulses $g_c(t)$ ist der PAKF–Verlauf zwischen zwei Abtastwerten $λ · T_c$ und $(λ + 1) · T_c$ stets linear. Entsprechend ist die periodische Kreuzkorrelationsfunktion (PKKF) zwischen den zwei unterschiedlichen Spreizfolgen $〈c_ν〉$ und $〈c_ν'〉$ gleicher Periodenlänge $P$ wie folgt gegeben: $\varphi_{cc'}(\lambda \cdot T_c) = \frac{1}{P}\cdot\sum\limits^{P-1}_{\nu = 0} c_\nu \cdot c\hspace{0.02cm}'_{\nu+ \lambda }\hspace{0.05cm}.$

Weitere Informationen zu diesem Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im Kapitel 9 (Programm „stp”) des Praktikums „Simulationsmethoden in der Nachrichtentechnik” am Lehrstuhl für Nachrichtentechnik der TU München. Diese Lehrveranstaltung basiert auf den 24 DOS–Programmen des Lehrsoftwarepaketes LNTsim.

Herunterladen des Programmpakets LNTsim (Zip–Version)

Herunterladen der dazugehörigen Texte (PDF–Datei) (PDF–Datei mit Kapitel 9)

Beurteilungskriterien für PN–Spreizfolgen

Die Qualität eines auf PN–Modulation basierenden CDMA–Systems hängt signifikant von den PAKF– und PKKF–Eigenschaften der verwendeten Spreizfolgen ab. Zusammenfassend kann man sagen:

Die PAKF der verwendeten Spreizcodeklasse sollte möglichst durch einen ausgeprägten Peak bei $λ =$ 0 gekennzeichnet sein, um die Synchronisation beim Empfänger einfach gestalten zu können. Bei Mehrwegeempfang mit einem Echo der Laufzeitdifferenz $λ · T_c$ ist zudem die Degradation aufgrund von Impulsinterferenzen um so geringer, je kleiner $|φ_c(λ · T_c)|$ ist.
Der störende Einfluss interferierender CDMA–Teilnehmer lässt sich durch den PKKF–Wert $φ_{cc'} (λ =$ 0) abschätzen. Ist dieser gleich 0, so spricht man von orthogonalen Funktionen. Die Fehlerwahrscheinlichkeit wird in diesem Fall nicht erhöht. Sind alle Spreizfolgen orthogonal, so ergibt sich auch bei $J$ Teilnehmern die gleiche Fehlerwahrscheinlichkeit wie bei nur einem Nutzer.
Diese letzte Aussage ist in synchronen Systemen mit verzerrungsfreiem Kanal (z.B. AWGN) von besonderer Bedeutung. Bei asynchronem Betrieb oder Mehrwegeempfang kommt es dagegen zu einer De–Orthogonalisierung und der strengeren Forderung, dass die PKKF zwischen den einzelnen Folgen zu allen Zeitpunkten (betragsmäßig) möglichst kleine Werte annehmen soll.
Bei der Auswahl von Codefamilien für ein CDMA–System ist weiter darauf zu achten, dass bei gegebenem Spreizgrad $J = P$ möglichst viele Codefolgen mit günstigen Eigenschaften hinsichtlich der obigen drei Punkte gefunden werden können, um somit auch möglichst viele Teilnehmer gleichzeitig im gleichen Frequenzband versorgen zu können.

PN–Folgen maximaler Länge (1)

Mit einem rückgekoppelten Schieberegister lässt sich eine Folge mit günstigen AKF–Eigenschaften erzeugen, wenn man die Rückführungskoeffizienten $g_i, i = 1, ... , G–1$ wählt. Die Folge $〈c_ν〉$ ist im strengen Sinne nicht zufällig, sondern periodisch. Aufgrund der großen Periodenlänge $P$ erscheint sie aber für einen unbedarften Betrachter als stochastisch. Man spricht von einer PN–Folge (Pseudo Noise).

PN–Generatoren haben folgende Eigenschaften, siehe Buch „Stochastische Signaltheorie”, Kapitel 2.5:

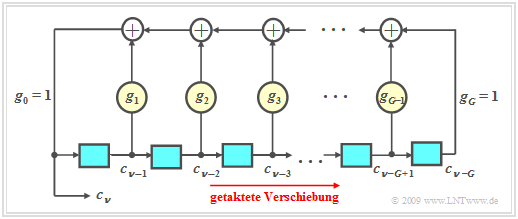
Die zu früheren Zeitpunkten generierten Binärwerte $c_{ν–1}, ... , c_{ν–G}$ sind in den $G$ Speicherzellen des Schieberegisters abgelegt. Man bezeichnet $G$ als den Grad des Schieberegisters.
Die Koeffizienten $g_1, ... , g_{G–1}$ sind Binärwerte, wobei eine „1” eine Rückkopplung an der entsprechenden Stelle des Schieberegisters kennzeichnet und eine „0” keine Rückführung.
Für das aktuell erzeugte Symbol gilt mit $g_i ∈$ {0, 1} und $i = 1, ... , G–1$ :

$c_\nu = (g_1\cdot c_{\nu-1}+g_2\cdot c_{\nu-2}+...+g_i\cdot c_{\nu-i}+...+g_{G-1}\cdot c_{\nu-G+1}+ c_{\nu-G})\hspace{0.1cm} \rm mod \hspace{0.2cm}2.$

Die Modulo–2–Addition kann zum Beispiel durch eine XOR–Verknüpfung realisiert werden:

$(x + y)\hspace{0.1cm} \rm mod\hspace{0.1cm}2 = {\it x}\hspace{0.1cm}\rm XOR\hspace{0.1cm} {\it y} = \left\{ \begin{array}{*{2}{c}} 0 & \rm falls\hspace{0.1cm} {\it x}= {\it y},\\ 1 & \rm falls\hspace{0.1cm} {\it x}\neq {\it y}. \\ \end{array} \right.$

Sind nicht alle $G$ Speicherzellen mit Nullen vorbelegt, so entsteht eine periodische Zufallsfolge $〈c_ν〉$ . Die Periodenlänge $P$ dieser Folge hängt stark von den Rückkopplungskoeffizienten $g_i$ ab.

Generatorpolynome von M–Sequenzen, G: Grad

Für jeden Grad $G$ gibt es zumindest zwei Konfigurationen mit der hierfür maximalen Periodenlänge $P_{\rm max} = 2^G – 1$ .

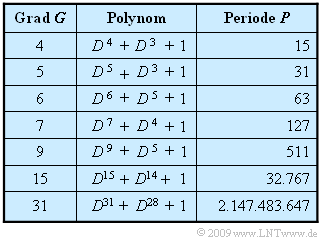
In nebenstehender Tabelle sind für einige Werte von $G$ das Generatorpolynom $G(D)$ einer solchen $M$ –Sequenz und die dazugehörige (maximale) Periodenlänge $P$ angegeben, wobei das „M” für „Maximal” steht. Im nächsten Abschnitt werden die hier gemachten Aussagen am Beispiel $G =$ 4 verdeutlicht.