Quadratur–Amplitudenmodulation

Inhaltsverzeichnis

1 Allgemeine Beschreibung und Signalraumzuordnung (1)
2 Allgemeine Beschreibung und Signalraumzuordnung (2)
3 Systembeschreibung durch das äquivalente TP–Signal
4 Leistung und Energie von QAM–Signalen
5 Signalverläufe der 4–QAM

Allgemeine Beschreibung und Signalraumzuordnung (1)

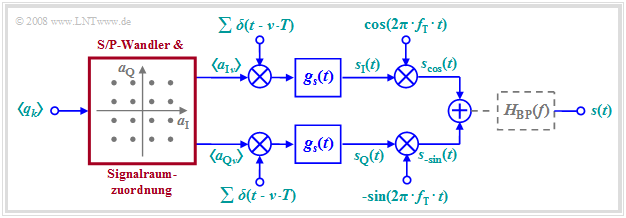
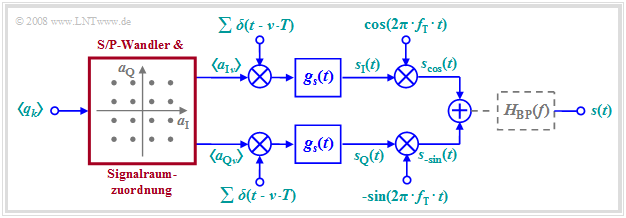
Aufgrund der Orthogonalität von Cosinus und (Minus–)Sinus kann man über einen Übertragungskanal zwei Datenströme unabhängig voneinander übertragen. Die Grafik zeigt das allgemeine Blockschaltbild.

Dieses sehr allgemeine Modell lässt sich wie folgt beschreiben:

Am Eingang liegt die binäre Quellensymbolfolge $〈q_k〉$ mit der Bitrate $R_{\rm B}$ an. Der zeitliche Abstand zweier Symbole ist damit $T_{\rm B} = 1/R_{\rm B}$ .
Aus jeweils $b$ binären Eingangssymbolen $q_k$ werden zwei mehrstufige Amplitudenkoeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ abgeleitet, wobei „I” für Inphase und „Q” für Quadraturkomponente steht.
Ist $b$ geradzahlig und die Signalraumzuordnung quadratisch, so können die Koeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ jeweils einen von $M = 2^{b/2}$ Amplitudenwerten mit gleicher Wahrscheinlichkeit annehmen. Man spricht dann von Quadratur–Amplitudenmodulation (QAM).
Das in der Grafik betrachtete Beispiel gilt für die 16–QAM mit $b = M =$ 4 und dementsprechend 16 Signalraumpunkten. Bei einer 256–QAM würde $b =$ 8 und $M =$ 16 gelten $(2^b = M^2 =$ 256).

Allgemeine Beschreibung und Signalraumzuordnung (2)

Fortsetzung der Bildbeschreibung zur obigen Grafik:

Anschließend werden die Koeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ jeweils einem Diracpuls als Impulsgewichte eingeprägt. Nach der Impulsformung mit dem Sendegrundimpuls $g_s(t)$ gilt somit in den beiden Zweigen des Blockschaltbildes:

$\begin{align*}s_{\rm I}(t) & = \sum_{\nu = - \infty}^{+\infty}a_{\rm I\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm},\\s_{\rm Q}(t) & = \sum_{\nu = - \infty}^{+\infty}a_{\rm Q\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm}.\end{align*}$

Anzumerken ist, dass wegen der redundanzfreien Umsetzung die Symboldauer $T$ dieser Signale um den Faktor $b$ größer ist als die Bitdauer $T_{\rm B}$ des binären Quellensignals. Im gezeichneten Beispiel (16-QAM) gilt $T = 4 · T_{\rm B}$ .
Das QAM–Sendesignal $s(t)$ ist dann die Summe der beiden mit Cosinus bzw. Minus–Sinus multiplizierten Teilsignale:

$\begin{align*}s_{\rm cos}(t) & = s_{\rm I}(t) \cdot \cos(2 \pi f_{\rm T} t),\\ s_{\rm -sin}(t) & = -s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t)\end{align*}$

Die beiden Übertragungszweige (I, Q) können als zwei völlig getrennte $M$ –stufige ASK–Systeme aufgefasst werden, die sich gegenseitig nicht stören, solange alle Komponenten optimal ausgelegt sind. Die Quadratur–Amplitudenmodulation ermöglicht somit (im Idealfall) eine Verdoppelung der Datenrate bei gleichbleibender Qualität.

Systembeschreibung durch das äquivalente TP–Signal

Da die Multiplikation von $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ mit einer Cosinus– bzw. Minus–Sinus–Schwingung nur eine Verschiebung im Frequenzbereich bewirkt und eine solche Verschiebung eine lineare Operation darstellt, lässt sich die Systembeschreibung mit Hilfe der äquivalenten TP–Signale wesentlich vereinfachen.

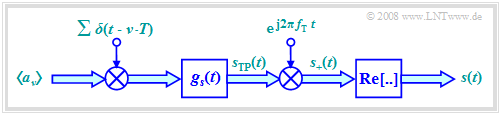
Die Grafik zeigt das vereinfachte Modell im Basisband. Dieses ist äquivalent zum bisher betrachteten Blockschaltbild. Beachten Sie bitte die folgenden Hinweise:

Die im Blockschaltbild rot gezeichnete Seriell–Parallel–Wandlung und die Signalraumzuordnung bleibt erhalten, obwohl dieser Block hier nicht mehr eingezeichnet ist. Lassen wir zunächst auch den oft aus schaltungstechnischen Gründen eingebrachten Bandpass $H_{\rm BP}(f)$ außer Betracht.
Alle Doppelpfeile in dem obigen Basisbandmodell kennzeichnen komplexe Größen. Die damit verbundenen Operationen sind ebenfalls komplex zu verstehen. Beispielsweise fasst der komplexe Amplitudenkoeffizient $a_ν$ je einen Inphase– und einen Quadraturkoeffizienten zusammen:

$a_\nu = a_{\rm I\hspace{0.03cm}\it \nu} + {\rm j} \cdot a_{\rm Q\hspace{0.03cm}\it \nu} \hspace{0.05cm}.$

Die äquivalente Tiefpass–Repräsentation des tatsächlichen, physikalischen und damit per se reellen Sendesignals $s(t)$ ist bei QAM stets komplex und es gilt mit den Teilsignalen $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ :

$s_{\rm TP}(t) = s_{\rm I}(t) + {\rm j} \cdot s_{\rm Q}(t) = \sum_{\nu = - \infty}^{+\infty} a_\nu \cdot g_s (t - \nu \cdot T)\hspace{0.05cm}.$

Zum analytischen Signal $s_+(t)$ kommt man von $s_{\rm TP}(t)$ durch Multiplikation mit der komplexen Exponentialfunktion. Das physikalische Sendesignal $s(t)$ ergibt sich dann als der Realteil von $s_+(t)$ .
Damit die Vorzeichen im Blockschaltbild der letzten Seite und im skizzierten Basisbandmodell übereinstimmen, ist im Quadraturzweig die Multiplikation mit der negativen Sinus–Schwingung erforderlich, wie die nachfolgende Rechnung zeigt:

$\begin{align*}s(t) & = {\rm Re}[s_{\rm +}(t)] = {\rm Re}[s_{\rm TP}(t) \cdot{\rm e}^{{\rm j}2\pi f_{\rm T} t}] = \\ & = {\rm Re} \left[\left ( \sum (a_{\rm I\hspace{0.03cm}\it \nu} + {\rm j} \cdot a_{\rm Q\hspace{0.03cm}\it \nu} ) \cdot g_s (t - \nu \cdot T)\right )\left ( \cos(2 \pi f_{\rm T} t) + {\rm j} \cdot \sin(2 \pi f_{\rm T} t) \right )\right]= \\ & = s_{\rm I}(t) \cdot \cos(2\pi f_{\rm T} t) - s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t) \hspace{0.05cm}.\end{align*}$

Der Einfluss des Bandpasses $H_{\rm BP}(f)$ , der in der Praxis oft am Ausgang des QAM–Modulators zu berücksichtigen ist, kann dem Impulsformfilter $g_s(t)$ beaufschlagt werden. Ist der Durchlassbereich des BP–Filters symmetrisch um $f_{\rm T}$ , so ist sein Tiefpass–Äquivalent (im Zeitbereich) $h_{\rm BP→TP}(t)$ rein reell und man kann im Modell $g_s(t)$ durch $g_s(t) \star h_{\rm BP→TP}(t)$ ersetzen.

Leistung und Energie von QAM–Signalen

Wie im Kapitel 4.3 von „Signaldarstellung” gezeigt wird, kann die Leistung des QAM–Sendesignals $s(t)$ auch aus dem äquivalenten TP–Signal $s_{\rm TP}(t)$ berechnet werden, das stets komplex ist: $P = \lim_{T_{\rm M} \rightarrow \infty} \frac{\rm 1}{T_{\rm M}}\cdot \int_{-T_{\rm M}/2}^{+T_{\rm M}/2} s(t)^2\,{\rm d} t = \frac{\rm 1}{2} \cdot \lim_{T_{\rm M} \rightarrow \infty} \frac{\rm 1}{T_{\rm M}}\cdot \int_{-T_{\rm M}/2}^{+T_{\rm M}/2} |s_{\rm TP}(t)|^2\,{\rm d} t \hspace{0.05cm}.$ Dagegen ist die Energie der Signale $s(t)$ und $s_{\rm TP}(t)$ unendlich groß. Beschränkt man sich jedoch auf eine Symboldauer $T$ , so erhält man die Energie pro Symbol $E_{\rm S} = \frac{{\rm E}[\hspace{0.05cm}|a_{\nu} |^2\hspace{0.05cm}]}{2}\cdot \int_{-\infty}^{+\infty} |g_s(t)|^2\,{\rm d} t = \frac{{\rm E}[|a_{\nu} |^2]}{2}\cdot \int_{-\infty}^{+\infty} |G_s(f)|^2\,{\rm d} f \hspace{0.05cm}.$ Dagegen gibt $E_{\rm B} = E_{\rm S}/b$ die Energie pro Bit an, wenn gemäß der gegebenen Signalraumzuordnung jeweils $b$ Binärsymbole zu einem komplexen Amplitudenkoeffizienten zusammengefasst werden.

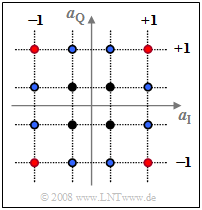
Die obere Grafik zeigt die Signalraumzuordnung bei 16–QAM, wobei sowohl der Real– als auch der Imaginärteil der komplexen Amplitudenkoeffizienten $a_ν$ jeweils einen von vier Werten (±1 sowie ±1/3) annehmen kann. Durch Mittelung über die 16 Abstandsquadrate zum Ursprung erhält man: $\begin{align*}{\rm E}[\hspace{0.05cm}|a_{\nu} |^2 \hspace{0.05cm}] \hspace{-0.18cm} & = \hspace{-0.18cm} \frac{4}{16} \cdot (1^2 + 1^2)+ \frac{4}{16} \cdot \left[({1}/{3} )^2 +({1}/{3})^2 \right ]+\\ \hspace{-0.18cm} & + \hspace{-0.18cm} \frac{8}{16} \cdot \left [1^2 + ({1}/{3})^2\right ] = ... \hspace{0.15cm}= \frac{10}{9}\approx 1.11 \hspace{0.05cm}.\end{align*}$

Die Summanden gehören in dieser Reihenfolge zu den vier roten, den vier schwarzen und den acht blauen Punkten.

Bei NRZ–rechteckförmigem Sendegrundimpuls $g_s(t)$ mit der Amplitude $g_0$ und der Symboldauer $T$ ist das Spektrum $G_s(f)$ si–förmig. In diesem Fall gilt für

die mittlere Energie pro Symbol:

$E_{\rm S} = \frac{{\rm E}[\hspace{0.05cm}|a_{\nu} |^2]\hspace{0.05cm}}{2}\cdot g_0^2 \cdot T = \frac{5}{9}\cdot g_0^2 \cdot T \hspace{0.05cm},$

die mittlere Energie pro Bit:

$E_{\rm B} = \frac{E_{\rm S}}{4}\approx 0.139 \cdot g_0^2 \cdot T \hspace{0.05cm}.$

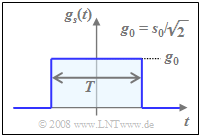
Die maximale Hüllkurve $s_0$ ist um den Faktor „Wurzel aus 2” größer als die Amplitude $g_0$ des Rechteckimpulses (siehe untere Skizze) und tritt bei einem der roten Amplitudenkoeffizienten auf, also immer dann, wenn $|a_{\rm Iν}| = |a_{\rm Qν}| =$ 1 ist.

Signalverläufe der 4–QAM

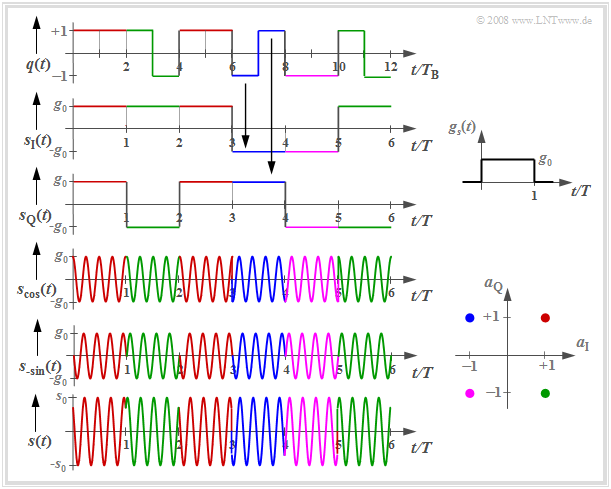
Die folgende Grafik zeigt die Signalverläufe der 4–QAM, wobei die Farbgebung mit der eingezeichneten Signalraumzuordnung übereinstimmt.

Man erkennt aus diesen Darstellungen:

die Seriell–Parallel–Wandlung des Quellensignals $q(t)$ in die beiden Komponentensignale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ , jeweils mit der Symboldauer $T = 2T_{\rm B}$ und den Signalwerten $±g_0 (T_{\rm B}$ ist die Bitdauer);
die beiden trägerfrequenzmodulierten Signale $s_{\rm cos}(t)$ und $s_{\rm –sin}(t)$ mit Phasensprüngen um $±π$ :

$s_{\rm cos} (t) = s_{\rm I} (t) \cdot \cos(2\pi f_{\rm T}t)\hspace{0.05cm},\hspace{0.2cm} s_{\rm -sin} (t) = -s_{\rm Q} (t) \cdot \sin(2\pi f_{\rm T}t)\hspace{0.05cm},$

das Sendesignal $s(t) = s_{\rm cos}(t) \ – \ s_{\rm –sin}(t)$ mit Phasensprüngen um Vielfache von $±π/2$ ; deren Hüllkurve ist gegenüber den beiden Komponentensignalen um den Faktor „Wurzel aus 2” größer:

$s_0 = \sqrt{2} \cdot g_0 \hspace{0.05cm}.$

Anzumerken ist, dass hier der Sendegrundimpuls $g_s(t)$ zur Vereinfachung der Darstellung im Bereich von 0 bis $T$ als rechteckförmig (also unsymmetrisch bezüglich $t =$ 0) angenommen wurde. Die zugehörige Spektralfunktion $G_s(f)$ dieses kausalen Impulses ist komplex, was jedoch in diesem Zusammenhang keine Auswirkungen hat.